Fast and Interpretable Consensus Clustering via Minipatch Learning

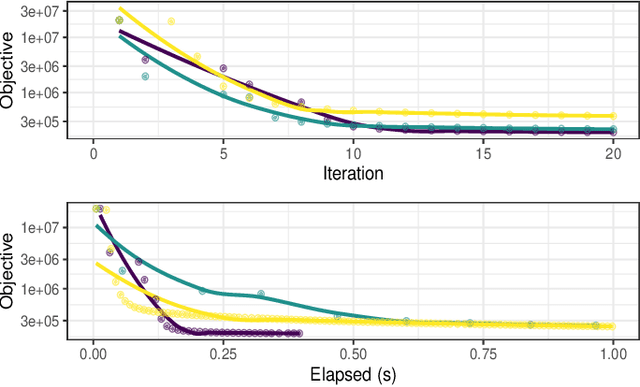
Consensus clustering has been widely used in bioinformatics and other applications to improve the accuracy, stability and reliability of clustering results. This approach ensembles cluster co-occurrences from multiple clustering runs on subsampled observations. For application to large-scale bioinformatics data, such as to discover cell types from single-cell sequencing data, for example, consensus clustering has two significant drawbacks: (i) computational inefficiency due to repeatedly applying clustering algorithms, and (ii) lack of interpretability into the important features for differentiating clusters. In this paper, we address these two challenges by developing IMPACC: Interpretable MiniPatch Adaptive Consensus Clustering. Our approach adopts three major innovations. We ensemble cluster co-occurrences from tiny subsets of both observations and features, termed minipatches, thus dramatically reducing computation time. Additionally, we develop adaptive sampling schemes for observations, which result in both improved reliability and computational savings, as well as adaptive sampling schemes of features, which leads to interpretable solutions by quickly learning the most relevant features that differentiate clusters. We study our approach on synthetic data and a variety of real large-scale bioinformatics data sets; results show that our approach not only yields more accurate and interpretable cluster solutions, but it also substantially improves computational efficiency compared to standard consensus clustering approaches.

Thresholded Graphical Lasso Adjusts for Latent Variables: Application to Functional Neural Connectivity

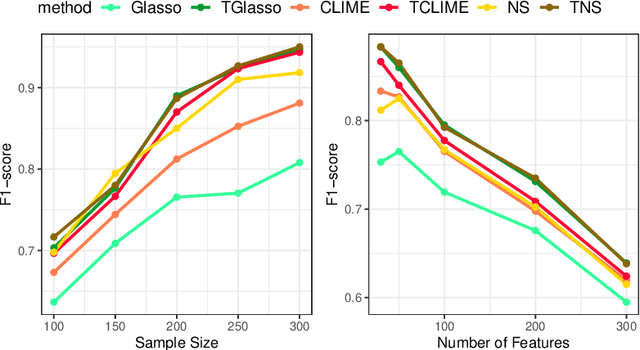
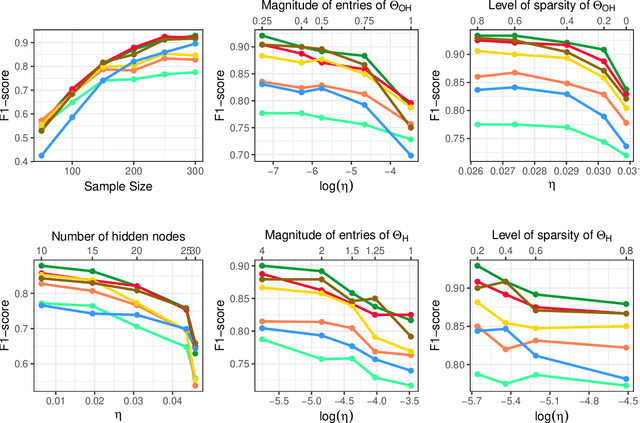
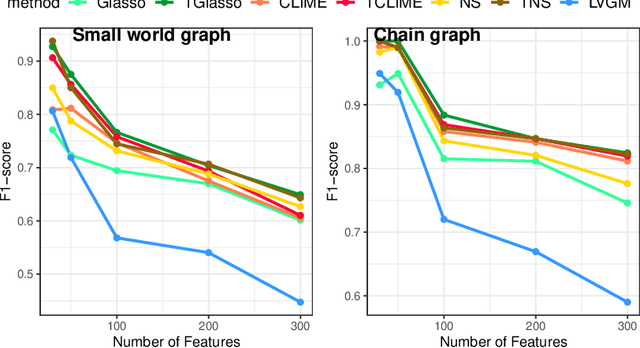
In neuroscience, researchers seek to uncover the connectivity of neurons from large-scale neural recordings or imaging; often people employ graphical model selection and estimation techniques for this purpose. But, existing technologies can only record from a small subset of neurons leading to a challenging problem of graph selection in the presence of extensive latent variables. Chandrasekaran et al. (2012) proposed a convex program to address this problem that poses challenges from both a computational and statistical perspective. To solve this problem, we propose an incredibly simple solution: apply a hard thresholding operator to existing graph selection methods. Conceptually simple and computationally attractive, we demonstrate that thresholding the graphical Lasso, neighborhood selection, or CLIME estimators have superior theoretical properties in terms of graph selection consistency as well as stronger empirical results than existing approaches for the latent variable graphical model problem. We also demonstrate the applicability of our approach through a neuroscience case study on calcium-imaging data to estimate functional neural connections.

Interpretable Visualization and Higher-Order Dimension Reduction for ECoG Data

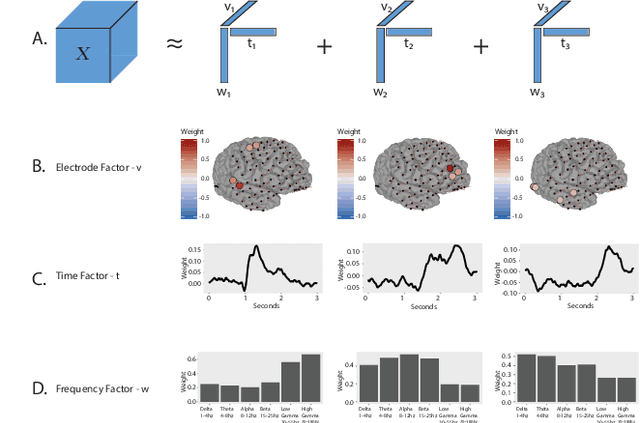
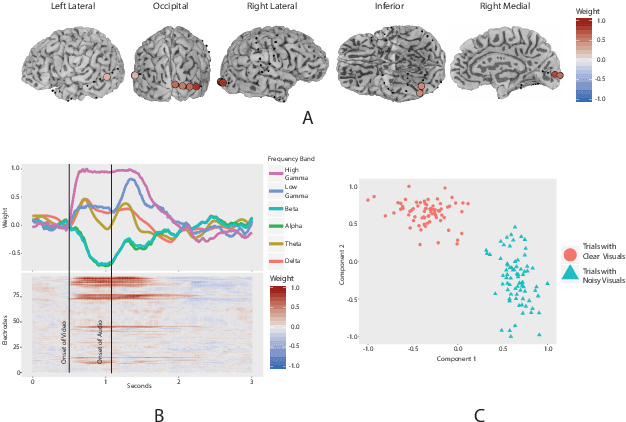
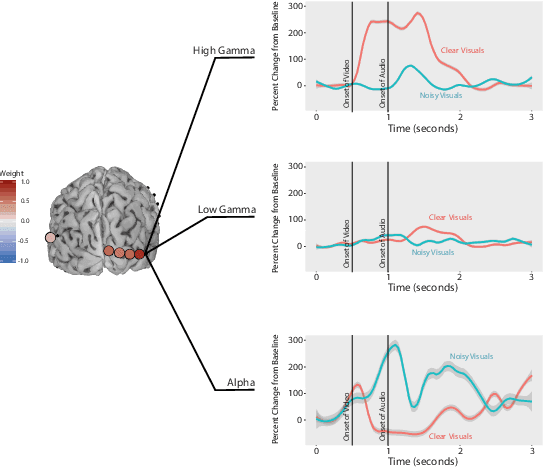
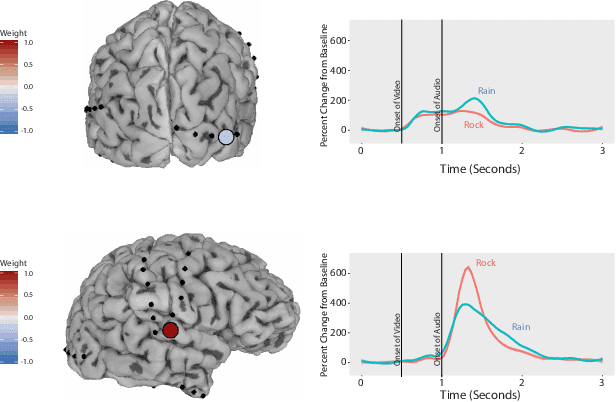
ElectroCOrticoGraphy (ECoG) technology measures electrical activity in the human brain via electrodes placed directly on the cortical surface during neurosurgery. Through its capability to record activity at a fast temporal resolution, ECoG experiments have allowed scientists to better understand how the human brain processes speech. By its nature, ECoG data is difficult for neuroscientists to directly interpret for two major reasons. Firstly, ECoG data tends to be large in size, as each individual experiment yields data up to several gigabytes. Secondly, ECoG data has a complex, higher-order nature. After signal processing, this type of data may be organized as a 4-way tensor with dimensions representing trials, electrodes, frequency, and time. In this paper, we develop an interpretable dimension reduction approach called Regularized Higher Order Principal Components Analysis, as well as an extension to Regularized Higher Order Partial Least Squares, that allows neuroscientists to explore and visualize ECoG data. Our approach employs a sparse and functional Candecomp-Parafac (CP) decomposition that incorporates sparsity to select relevant electrodes and frequency bands, as well as smoothness over time and frequency, yielding directly interpretable factors. We demonstrate the performance and interpretability of our method with an ECoG case study on audio and visual processing of human speech.

Simultaneous Grouping and Denoising via Sparse Convex Wavelet Clustering

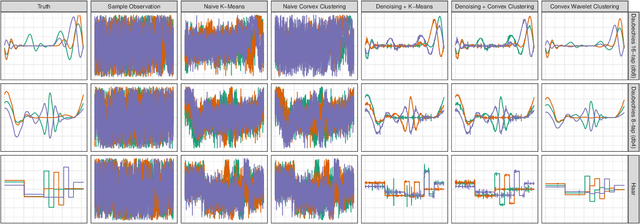
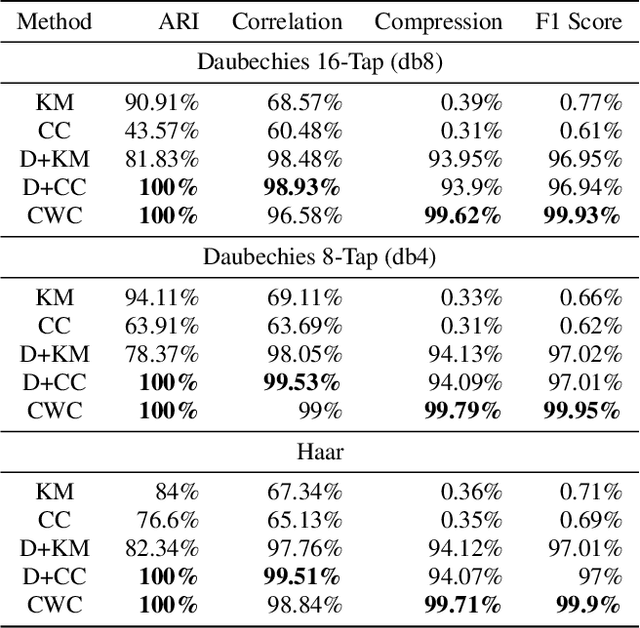
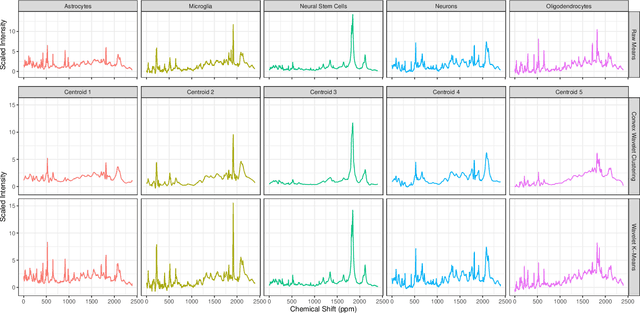
Clustering is a ubiquitous problem in data science and signal processing. In many applications where we observe noisy signals, it is common practice to first denoise the data, perhaps using wavelet denoising, and then to apply a clustering algorithm. In this paper, we develop a sparse convex wavelet clustering approach that simultaneously denoises and discovers groups. Our approach utilizes convex fusion penalties to achieve agglomeration and group-sparse penalties to denoise through sparsity in the wavelet domain. In contrast to common practice which denoises then clusters, our method is a unified, convex approach that performs both simultaneously. Our method yields denoised (wavelet-sparse) cluster centroids that both improve interpretability and data compression. We demonstrate our method on synthetic examples and in an application to NMR spectroscopy.

MP-Boost: Minipatch Boosting via Adaptive Feature and Observation Sampling

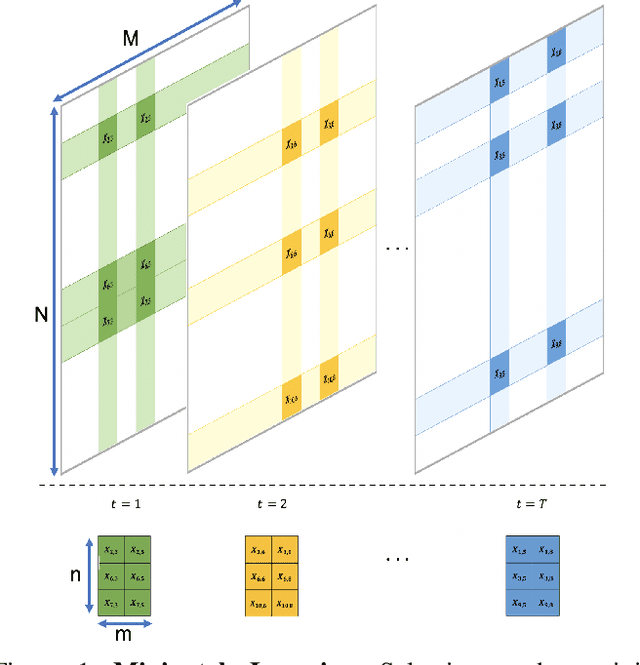
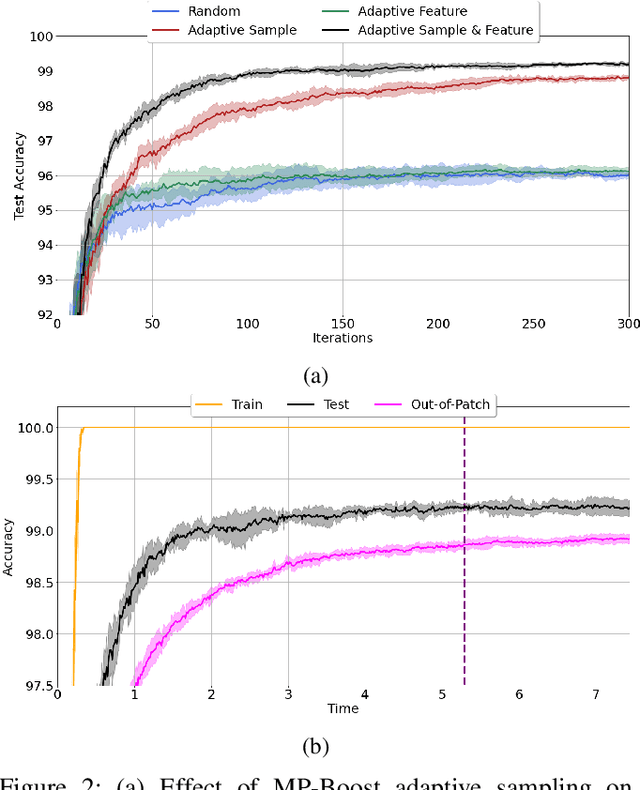
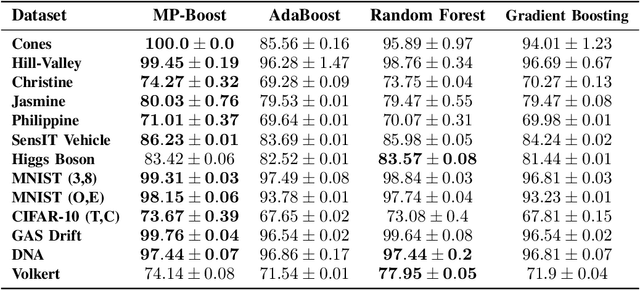
Boosting methods are among the best general-purpose and off-the-shelf machine learning approaches, gaining widespread popularity. In this paper, we seek to develop a boosting method that yields comparable accuracy to popular AdaBoost and gradient boosting methods, yet is faster computationally and whose solution is more interpretable. We achieve this by developing MP-Boost, an algorithm loosely based on AdaBoost that learns by adaptively selecting small subsets of instances and features, or what we term minipatches (MP), at each iteration. By sequentially learning on tiny subsets of the data, our approach is computationally faster than other classic boosting algorithms. Also as it progresses, MP-Boost adaptively learns a probability distribution on the features and instances that upweight the most important features and challenging instances, hence adaptively selecting the most relevant minipatches for learning. These learned probability distributions also aid in interpretation of our method. We empirically demonstrate the interpretability, comparative accuracy, and computational time of our approach on a variety of binary classification tasks.

Feature Selection for Huge Data via Minipatch Learning

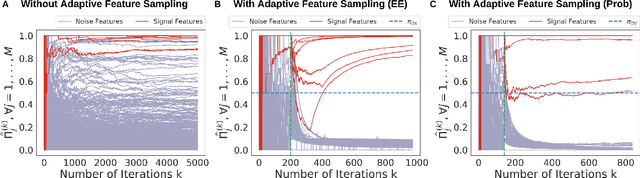
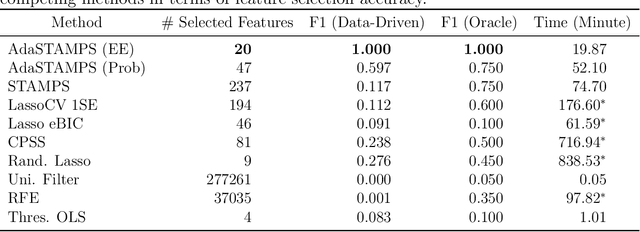
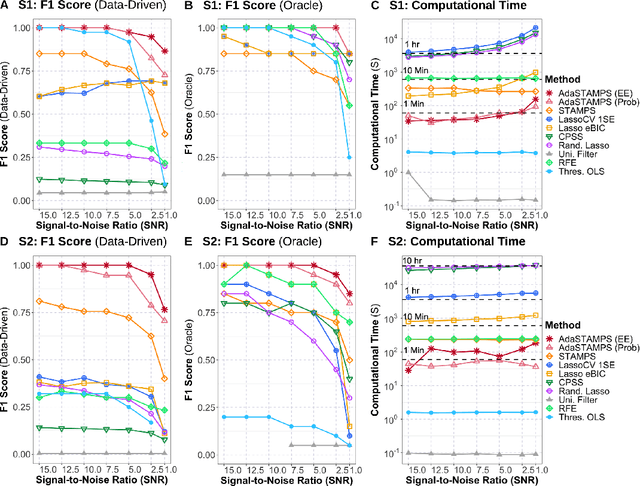
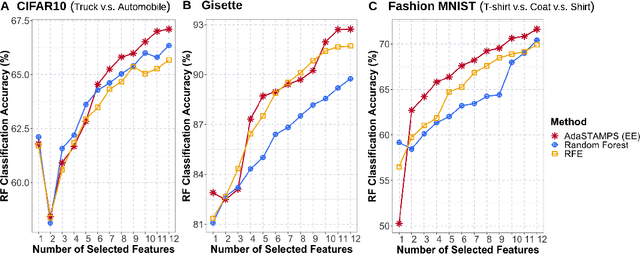
Feature selection often leads to increased model interpretability, faster computation, and improved model performance by discarding irrelevant or redundant features. While feature selection is a well-studied problem with many widely-used techniques, there are typically two key challenges: i) many existing approaches become computationally intractable in huge-data settings with millions of observations and features; and ii) the statistical accuracy of selected features degrades in high-noise, high-correlation settings, thus hindering reliable model interpretation. We tackle these problems by proposing Stable Minipatch Selection (STAMPS) and Adaptive STAMPS (AdaSTAMPS). These are meta-algorithms that build ensembles of selection events of base feature selectors trained on many tiny, (adaptively-chosen) random subsets of both the observations and features of the data, which we call minipatches. Our approaches are general and can be employed with a variety of existing feature selection strategies and machine learning techniques. In addition, we provide theoretical insights on STAMPS and empirically demonstrate that our approaches, especially AdaSTAMPS, dominate competing methods in terms of feature selection accuracy and computational time.

Supervised Convex Clustering

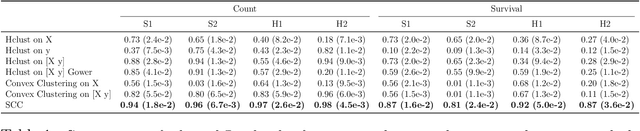
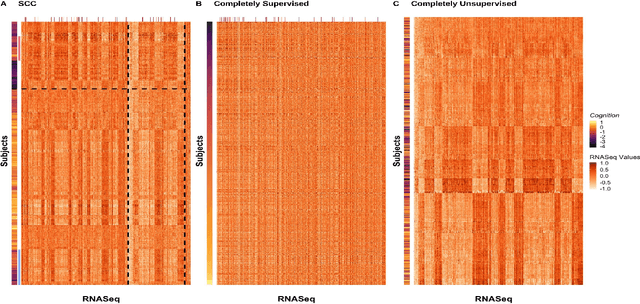
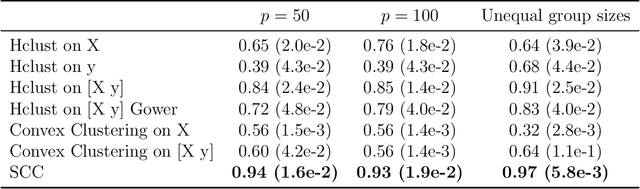
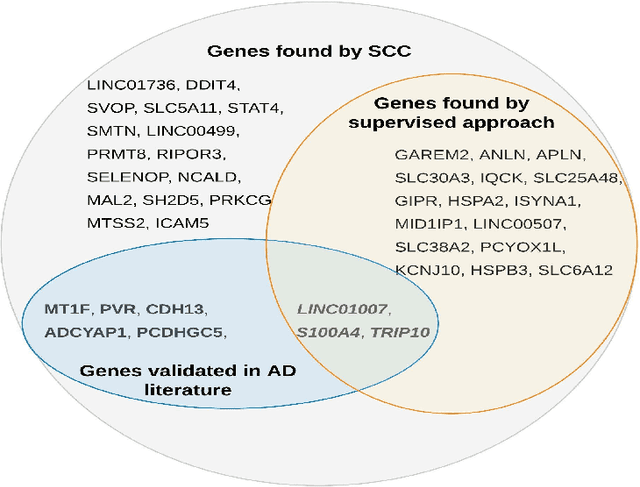
Clustering has long been a popular unsupervised learning approach to identify groups of similar objects and discover patterns from unlabeled data in many applications. Yet, coming up with meaningful interpretations of the estimated clusters has often been challenging precisely due to its unsupervised nature. Meanwhile, in many real-world scenarios, there are some noisy supervising auxiliary variables, for instance, subjective diagnostic opinions, that are related to the observed heterogeneity of the unlabeled data. By leveraging information from both supervising auxiliary variables and unlabeled data, we seek to uncover more scientifically interpretable group structures that may be hidden by completely unsupervised analyses. In this work, we propose and develop a new statistical pattern discovery method named Supervised Convex Clustering (SCC) that borrows strength from both information sources and guides towards finding more interpretable patterns via a joint convex fusion penalty. We develop several extensions of SCC to integrate different types of supervising auxiliary variables, to adjust for additional covariates, and to find biclusters. We demonstrate the practical advantages of SCC through simulations and a case study on Alzheimer's Disease genomics. Specifically, we discover new candidate genes as well as new subtypes of Alzheimer's Disease that can potentially lead to better understanding of the underlying genetic mechanisms responsible for the observed heterogeneity of cognitive decline in older adults.

Integrative Generalized Convex Clustering Optimization and Feature Selection for Mixed Multi-View Data

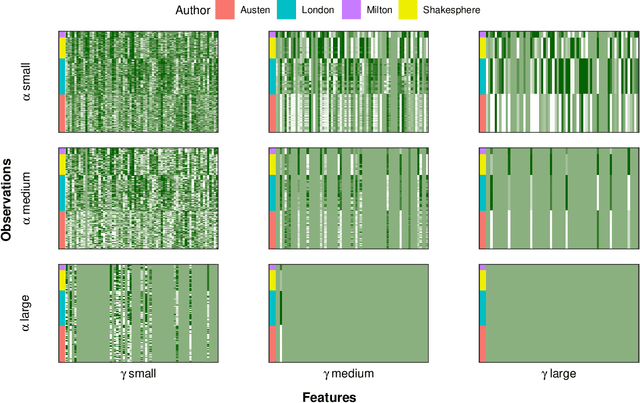
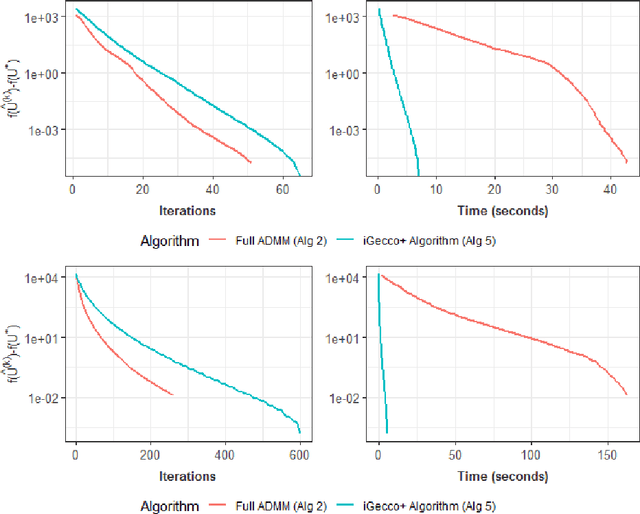
In mixed multi-view data, multiple sets of diverse features are measured on the same set of samples. By integrating all available data sources, we seek to discover common group structure among the samples that may be hidden in individualistic cluster analyses of a single data-view. While several techniques for such integrative clustering have been explored, we propose and develop a convex formalization that will inherit the strong statistical, mathematical and empirical properties of increasingly popular convex clustering methods. Specifically, our Integrative Generalized Convex Clustering Optimization (iGecco) method employs different convex distances, losses, or divergences for each of the different data views with a joint convex fusion penalty that leads to common groups. Additionally, integrating mixed multi-view data is often challenging when each data source is high-dimensional. To perform feature selection in such scenarios, we develop an adaptive shifted group-lasso penalty that selects features by shrinking them towards their loss-specific centers. Our so-called iGecco+ approach selects features from each data-view that are best for determining the groups, often leading to improved integrative clustering. To fit our model, we develop a new type of generalized multi-block ADMM algorithm using sub-problem approximations that more efficiently fits our model for big data sets. Through a series of numerical experiments and real data examples on text mining and genomics, we show that iGecco+ achieves superior empirical performance for high-dimensional mixed multi-view data.

Clustered Gaussian Graphical Model via Symmetric Convex Clustering

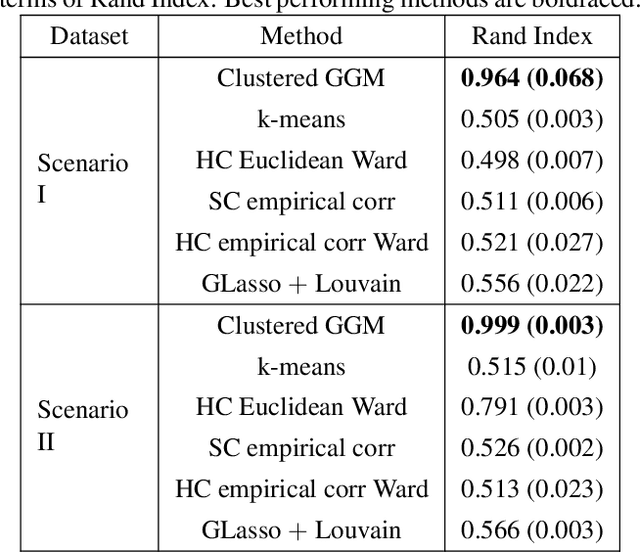
Knowledge of functional groupings of neurons can shed light on structures of neural circuits and is valuable in many types of neuroimaging studies. However, accurately determining which neurons carry out similar neurological tasks via controlled experiments is both labor-intensive and prohibitively expensive on a large scale. Thus, it is of great interest to cluster neurons that have similar connectivity profiles into functionally coherent groups in a data-driven manner. In this work, we propose the clustered Gaussian graphical model (GGM) and a novel symmetric convex clustering penalty in an unified convex optimization framework for inferring functional clusters among neurons from neural activity data. A parallelizable multi-block Alternating Direction Method of Multipliers (ADMM) algorithm is used to solve the corresponding convex optimization problem. In addition, we establish convergence guarantees for the proposed ADMM algorithm. Experimental results on both synthetic data and real-world neuroscientific data demonstrate the effectiveness of our approach.

Feature Selection for Data Integration with Mixed Multi-view Data

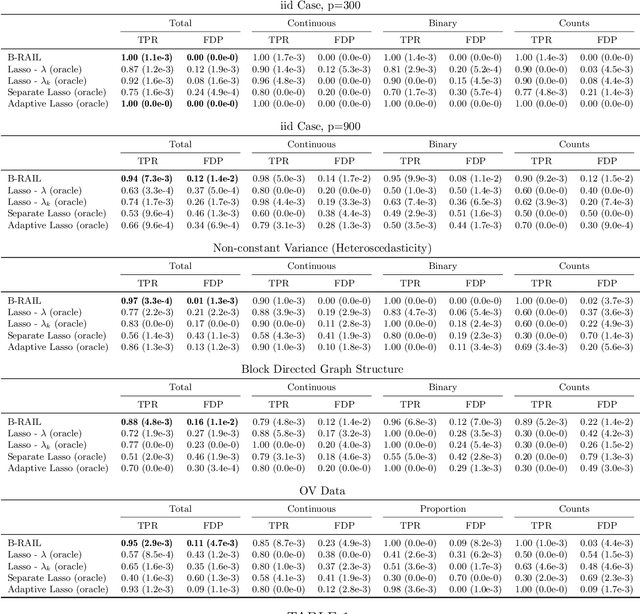
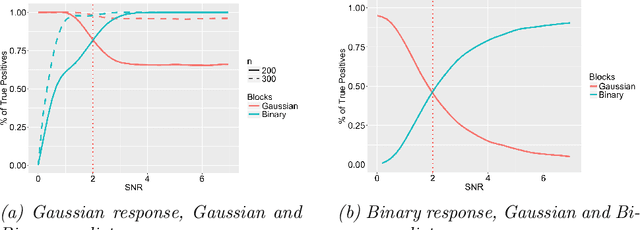
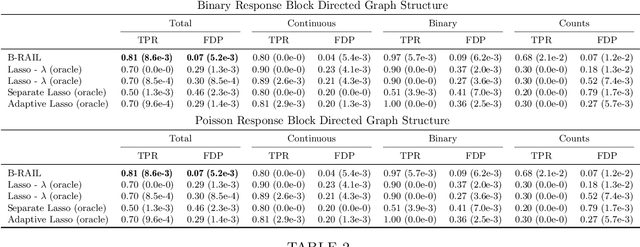
Data integration methods that analyze multiple sources of data simultaneously can often provide more holistic insights than can separate inquiries of each data source. Motivated by the advantages of data integration in the era of "big data", we investigate feature selection for high-dimensional multi-view data with mixed data types (e.g. continuous, binary, count-valued). This heterogeneity of multi-view data poses numerous challenges for existing feature selection methods. However, after critically examining these issues through empirical and theoretically-guided lenses, we develop a practical solution, the Block Randomized Adaptive Iterative Lasso (B-RAIL), which combines the strengths of the randomized Lasso, adaptive weighting schemes, and stability selection. B-RAIL serves as a versatile data integration method for sparse regression and graph selection, and we demonstrate the effectiveness of B-RAIL through extensive simulations and a case study to infer the ovarian cancer gene regulatory network. In this case study, B-RAIL successfully identifies well-known biomarkers associated with ovarian cancer and hints at novel candidates for future ovarian cancer research.