Differentially Private Bayesian Linear Regression

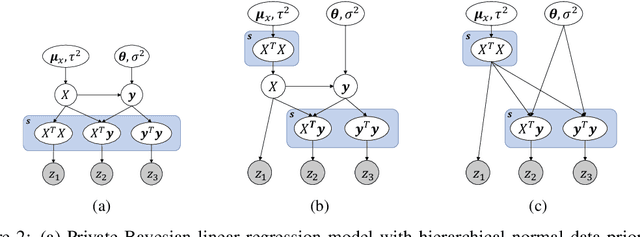
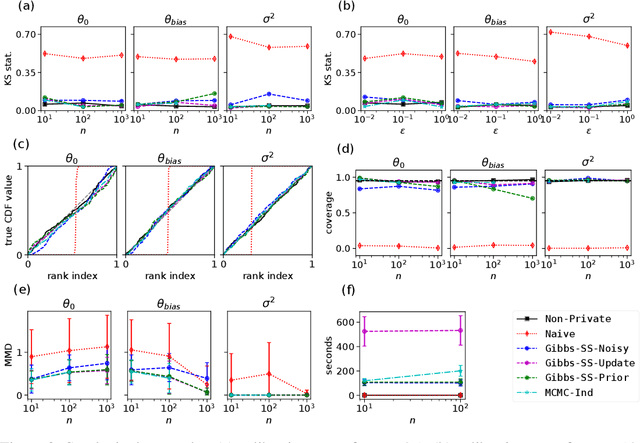
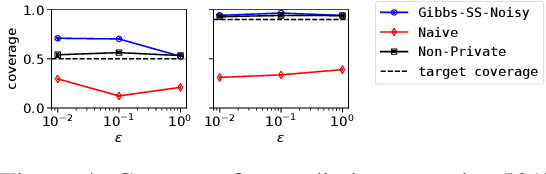
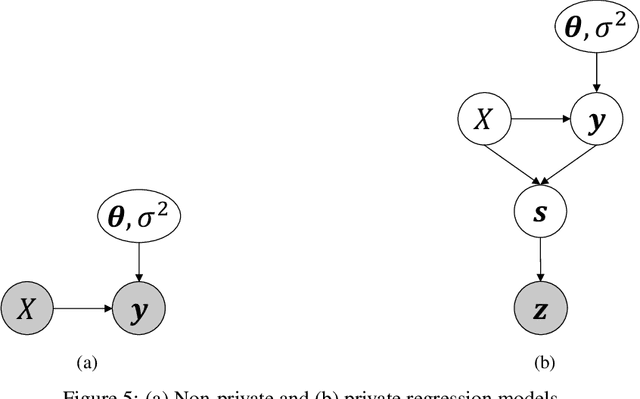
Linear regression is an important tool across many fields that work with sensitive human-sourced data. Significant prior work has focused on producing differentially private point estimates, which provide a privacy guarantee to individuals while still allowing modelers to draw insights from data by estimating regression coefficients. We investigate the problem of Bayesian linear regression, with the goal of computing posterior distributions that correctly quantify uncertainty given privately released statistics. We show that a naive approach that ignores the noise injected by the privacy mechanism does a poor job in realistic data settings. We then develop noise-aware methods that perform inference over the privacy mechanism and produce correct posteriors across a wide range of scenarios.

Differentially Private Bayesian Inference for Exponential Families

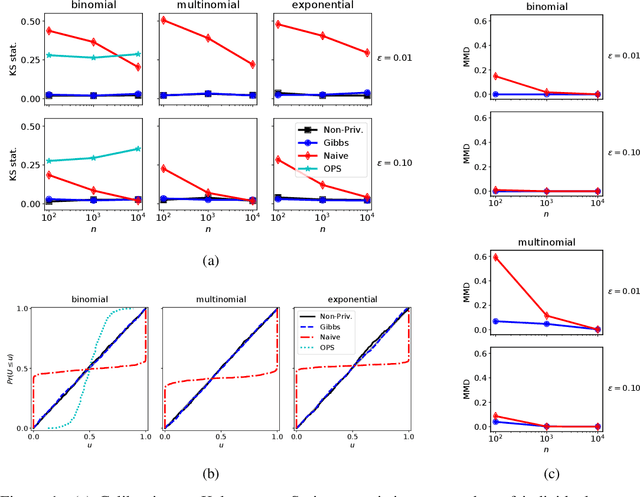
The study of private inference has been sparked by growing concern regarding the analysis of data when it stems from sensitive sources. We present the first method for private Bayesian inference in exponential families that properly accounts for noise introduced by the privacy mechanism. It is efficient because it works only with sufficient statistics and not individual data. Unlike other methods, it gives properly calibrated posterior beliefs in the non-asymptotic data regime.

Differentially Private Learning of Undirected Graphical Models using Collective Graphical Models

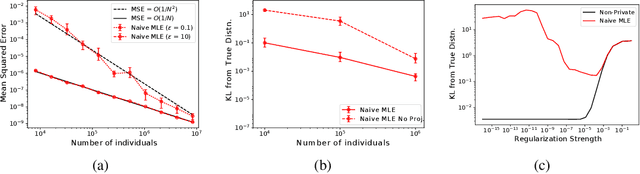
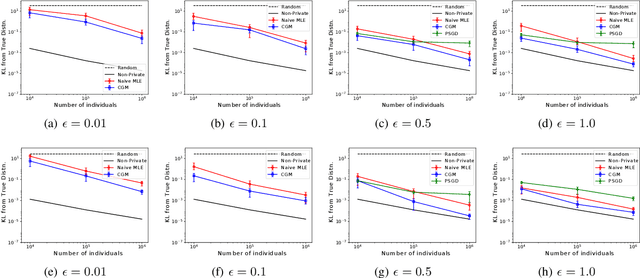
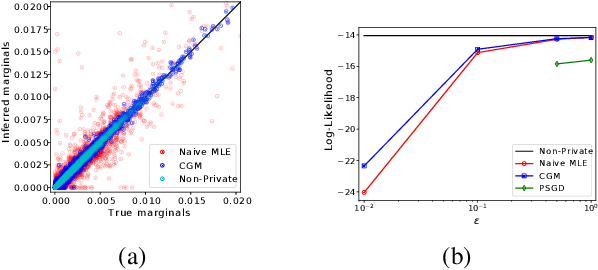
We investigate the problem of learning discrete, undirected graphical models in a differentially private way. We show that the approach of releasing noisy sufficient statistics using the Laplace mechanism achieves a good trade-off between privacy, utility, and practicality. A naive learning algorithm that uses the noisy sufficient statistics "as is" outperforms general-purpose differentially private learning algorithms. However, it has three limitations: it ignores knowledge about the data generating process, rests on uncertain theoretical foundations, and exhibits certain pathologies. We develop a more principled approach that applies the formalism of collective graphical models to perform inference over the true sufficient statistics within an expectation-maximization framework. We show that this learns better models than competing approaches on both synthetic data and on real human mobility data used as a case study.

Consistently Estimating Markov Chains with Noisy Aggregate Data

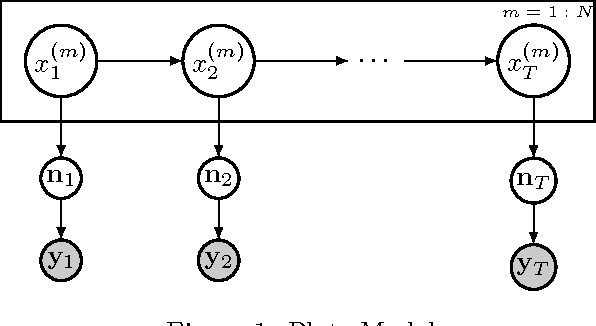
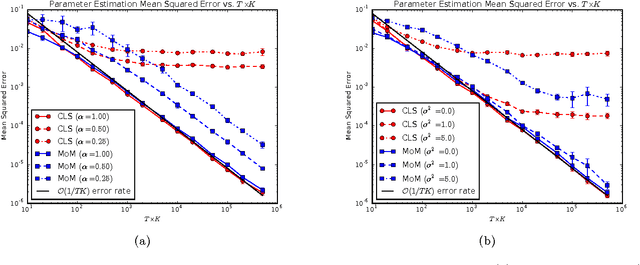
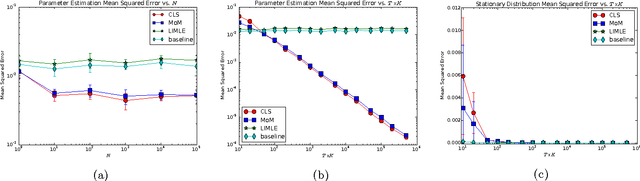
We address the problem of estimating the parameters of a time-homogeneous Markov chain given only noisy, aggregate data. This arises when a population of individuals behave independently according to a Markov chain, but individual sample paths cannot be observed due to limitations of the observation process or the need to protect privacy. Instead, only population-level counts of the number of individuals in each state at each time step are available. When these counts are exact, a conditional least squares (CLS) estimator is known to be consistent and asymptotically normal. We initiate the study of method of moments estimators for this problem to handle the more realistic case when observations are additionally corrupted by noise. We show that CLS can be interpreted as a simple "plug-in" method of moments estimator. However, when observations are noisy, it is not consistent because it fails to account for additional variance introduced by the noise. We develop a new, simpler method of moments estimator that bypasses this problem and is consistent under noisy observations.

Bayesian Discovery of Threat Networks

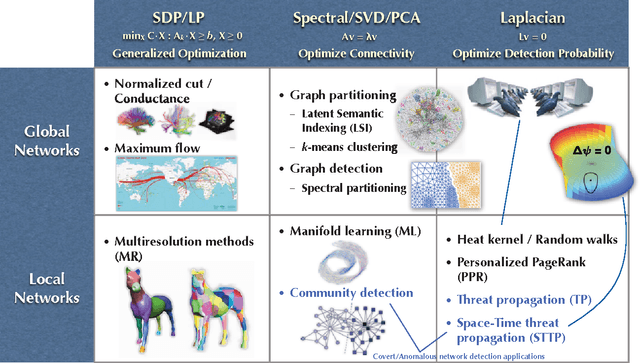
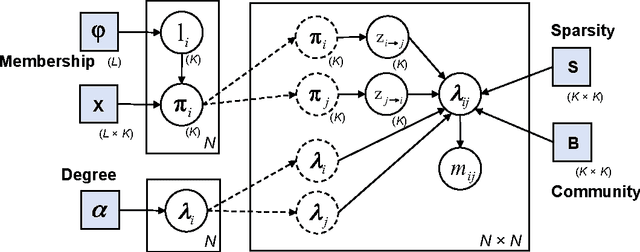
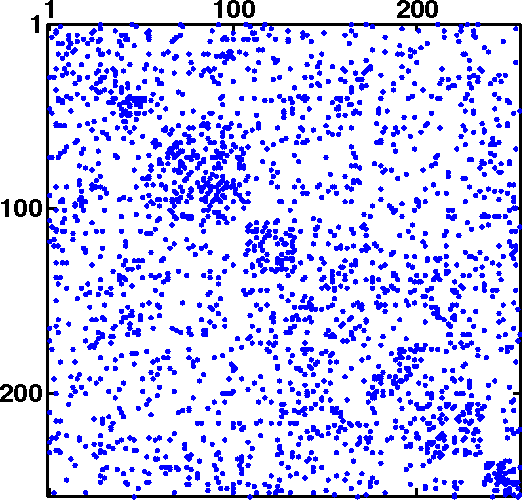
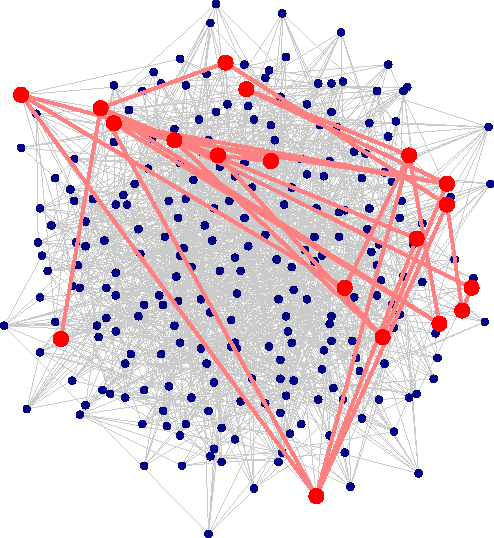
A novel unified Bayesian framework for network detection is developed, under which a detection algorithm is derived based on random walks on graphs. The algorithm detects threat networks using partial observations of their activity, and is proved to be optimum in the Neyman-Pearson sense. The algorithm is defined by a graph, at least one observation, and a diffusion model for threat. A link to well-known spectral detection methods is provided, and the equivalence of the random walk and harmonic solutions to the Bayesian formulation is proven. A general diffusion model is introduced that utilizes spatio-temporal relationships between vertices, and is used for a specific space-time formulation that leads to significant performance improvements on coordinated covert networks. This performance is demonstrated using a new hybrid mixed-membership blockmodel introduced to simulate random covert networks with realistic properties.

Network Detection Theory and Performance

Network detection is an important capability in many areas of applied research in which data can be represented as a graph of entities and relationships. Oftentimes the object of interest is a relatively small subgraph in an enormous, potentially uninteresting background. This aspect characterizes network detection as a "big data" problem. Graph partitioning and network discovery have been major research areas over the last ten years, driven by interest in internet search, cyber security, social networks, and criminal or terrorist activities. The specific problem of network discovery is addressed as a special case of graph partitioning in which membership in a small subgraph of interest must be determined. Algebraic graph theory is used as the basis to analyze and compare different network detection methods. A new Bayesian network detection framework is introduced that partitions the graph based on prior information and direct observations. The new approach, called space-time threat propagation, is proved to maximize the probability of detection and is therefore optimum in the Neyman-Pearson sense. This optimality criterion is compared to spectral community detection approaches which divide the global graph into subsets or communities with optimal connectivity properties. We also explore a new generative stochastic model for covert networks and analyze using receiver operating characteristics the detection performance of both classes of optimal detection techniques.