On the Implicit Bias in Deep-Learning Algorithms

Gradient-based deep-learning algorithms exhibit remarkable performance in practice, but it is not well-understood why they are able to generalize despite having more parameters than training examples. It is believed that implicit bias is a key factor in their ability to generalize, and hence it has been widely studied in recent years. In this short survey, we explain the notion of implicit bias, review main results and discuss their implications.

Reconstructing Training Data from Trained Neural Networks

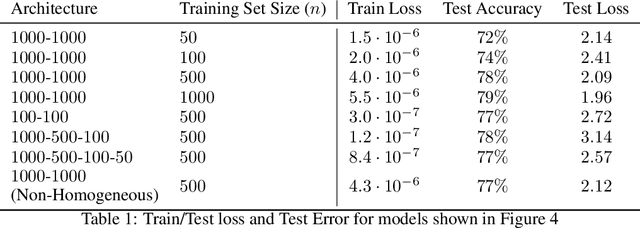
Understanding to what extent neural networks memorize training data is an intriguing question with practical and theoretical implications. In this paper we show that in some cases a significant fraction of the training data can in fact be reconstructed from the parameters of a trained neural network classifier. We propose a novel reconstruction scheme that stems from recent theoretical results about the implicit bias in training neural networks with gradient-based methods. To the best of our knowledge, our results are the first to show that reconstructing a large portion of the actual training samples from a trained neural network classifier is generally possible. This has negative implications on privacy, as it can be used as an attack for revealing sensitive training data. We demonstrate our method for binary MLP classifiers on a few standard computer vision datasets.

On the Effective Number of Linear Regions in Shallow Univariate ReLU Networks: Convergence Guarantees and Implicit Bias

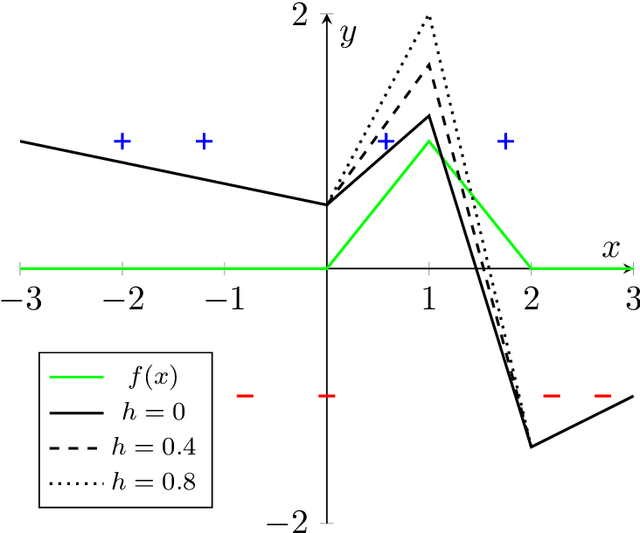
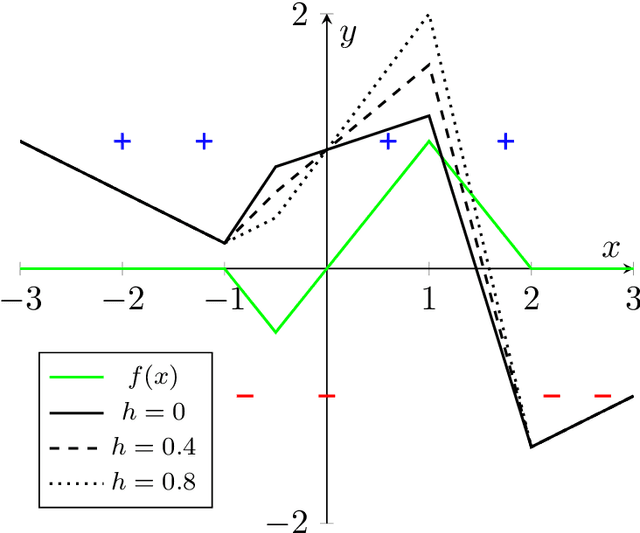
We study the dynamics and implicit bias of gradient flow (GF) on univariate ReLU neural networks with a single hidden layer in a binary classification setting. We show that when the labels are determined by the sign of a target network with $r$ neurons, with high probability over the initialization of the network and the sampling of the dataset, GF converges in direction (suitably defined) to a network achieving perfect training accuracy and having at most $\mathcal{O}(r)$ linear regions, implying a generalization bound. Our result may already hold for mild over-parameterization, where the width is $\tilde{\mathcal{O}}(r)$ and independent of the sample size.

The Sample Complexity of One-Hidden-Layer Neural Networks

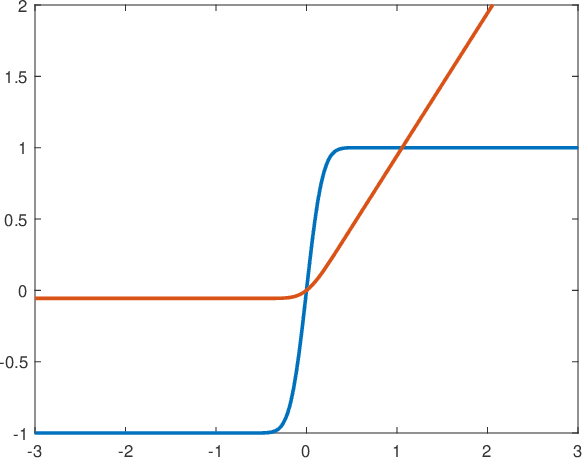
We study norm-based uniform convergence bounds for neural networks, aiming at a tight understanding of how these are affected by the architecture and type of norm constraint, for the simple class of scalar-valued one-hidden-layer networks, and inputs bounded in Euclidean norm. We begin by proving that in general, controlling the spectral norm of the hidden layer weight matrix is insufficient to get uniform convergence guarantees (independent of the network width), while a stronger Frobenius norm control is sufficient, extending and improving on previous work. Motivated by the proof constructions, we identify and analyze two important settings where a mere spectral norm control turns out to be sufficient: First, when the network's activation functions are sufficiently smooth (with the result extending to deeper networks); and second, for certain types of convolutional networks. In the latter setting, we study how the sample complexity is additionally affected by parameters such as the amount of overlap between patches and the overall number of patches.

Gradient Methods Provably Converge to Non-Robust Networks

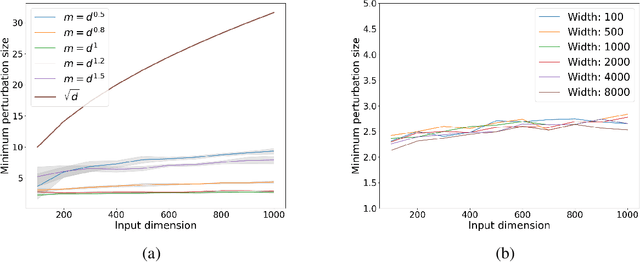
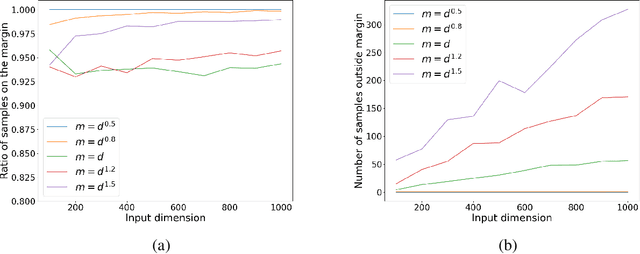
Despite a great deal of research, it is still unclear why neural networks are so susceptible to adversarial examples. In this work, we identify natural settings where depth-$2$ ReLU networks trained with gradient flow are provably non-robust (susceptible to small adversarial $\ell_2$-perturbations), even when robust networks that classify the training dataset correctly exist. Perhaps surprisingly, we show that the well-known implicit bias towards margin maximization induces bias towards non-robust networks, by proving that every network which satisfies the KKT conditions of the max-margin problem is non-robust.

Width is Less Important than Depth in ReLU Neural Networks

We solve an open question from Lu et al. (2017), by showing that any target network with inputs in $\mathbb{R}^d$ can be approximated by a width $O(d)$ network (independent of the target network's architecture), whose number of parameters is essentially larger only by a linear factor. In light of previous depth separation theorems, which imply that a similar result cannot hold when the roles of width and depth are interchanged, it follows that depth plays a more significant role than width in the expressive power of neural networks. We extend our results to constructing networks with bounded weights, and to constructing networks with width at most $d+2$, which is close to the minimal possible width due to previous lower bounds. Both of these constructions cause an extra polynomial factor in the number of parameters over the target network. We also show an exact representation of wide and shallow networks using deep and narrow networks which, in certain cases, does not increase the number of parameters over the target network.

Implicit Regularization Towards Rank Minimization in ReLU Networks

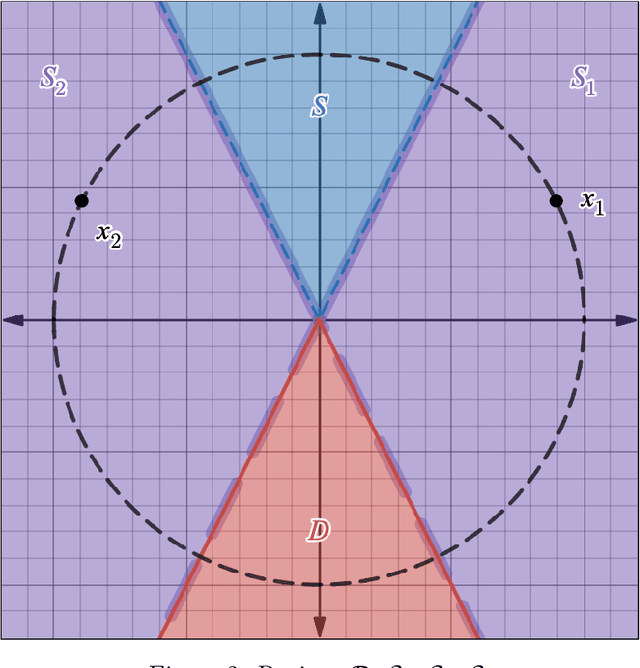
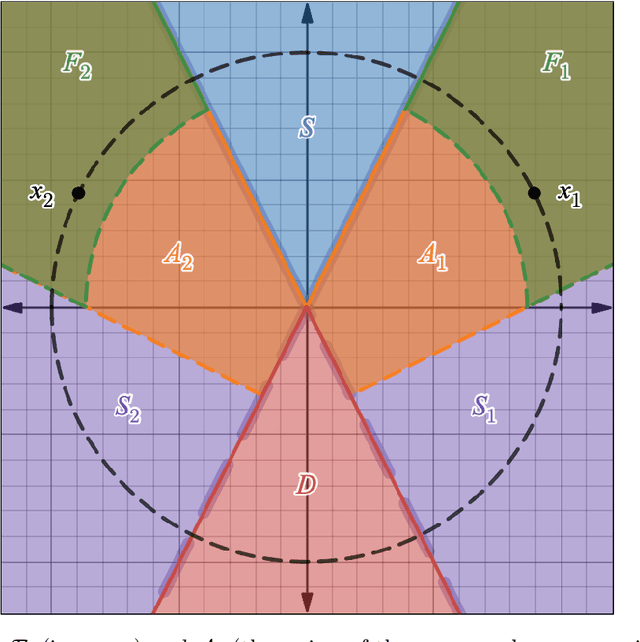
We study the conjectured relationship between the implicit regularization in neural networks, trained with gradient-based methods, and rank minimization of their weight matrices. Previously, it was proved that for linear networks (of depth 2 and vector-valued outputs), gradient flow (GF) w.r.t. the square loss acts as a rank minimization heuristic. However, understanding to what extent this generalizes to nonlinear networks is an open problem. In this paper, we focus on nonlinear ReLU networks, providing several new positive and negative results. On the negative side, we prove (and demonstrate empirically) that, unlike the linear case, GF on ReLU networks may no longer tend to minimize ranks, in a rather strong sense (even approximately, for "most" datasets of size 2). On the positive side, we reveal that ReLU networks of sufficient depth are provably biased towards low-rank solutions in several reasonable settings.

On Margin Maximization in Linear and ReLU Networks

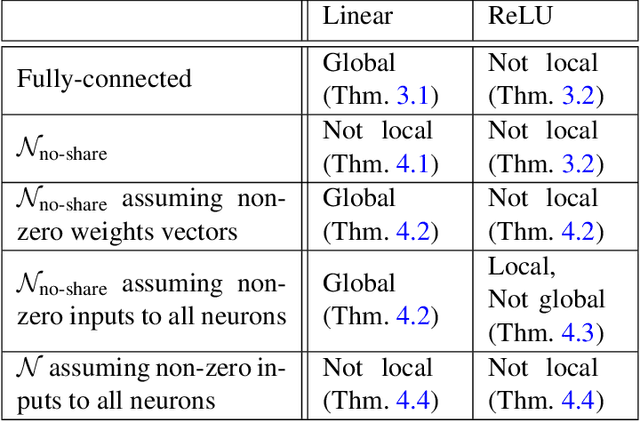
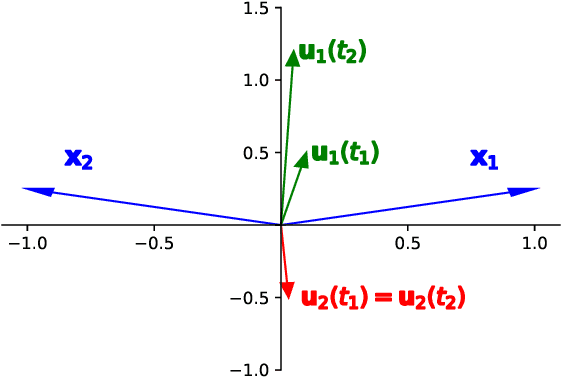
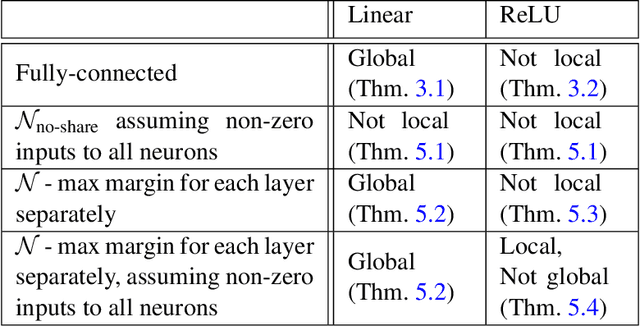
The implicit bias of neural networks has been extensively studied in recent years. Lyu and Li [2019] showed that in homogeneous networks trained with the exponential or the logistic loss, gradient flow converges to a KKT point of the max margin problem in the parameter space. However, that leaves open the question of whether this point will generally be an actual optimum of the max margin problem. In this paper, we study this question in detail, for several neural network architectures involving linear and ReLU activations. Perhaps surprisingly, we show that in many cases, the KKT point is not even a local optimum of the max margin problem. On the flip side, we identify multiple settings where a local or global optimum can be guaranteed. Finally, we answer a question posed in Lyu and Li [2019] by showing that for non-homogeneous networks, the normalized margin may strictly decrease over time.

On the Optimal Memorization Power of ReLU Neural Networks

We study the memorization power of feedforward ReLU neural networks. We show that such networks can memorize any $N$ points that satisfy a mild separability assumption using $\tilde{O}\left(\sqrt{N}\right)$ parameters. Known VC-dimension upper bounds imply that memorizing $N$ samples requires $\Omega(\sqrt{N})$ parameters, and hence our construction is optimal up to logarithmic factors. We also give a generalized construction for networks with depth bounded by $1 \leq L \leq \sqrt{N}$, for memorizing $N$ samples using $\tilde{O}(N/L)$ parameters. This bound is also optimal up to logarithmic factors. Our construction uses weights with large bit complexity. We prove that having such a large bit complexity is both necessary and sufficient for memorization with a sub-linear number of parameters.

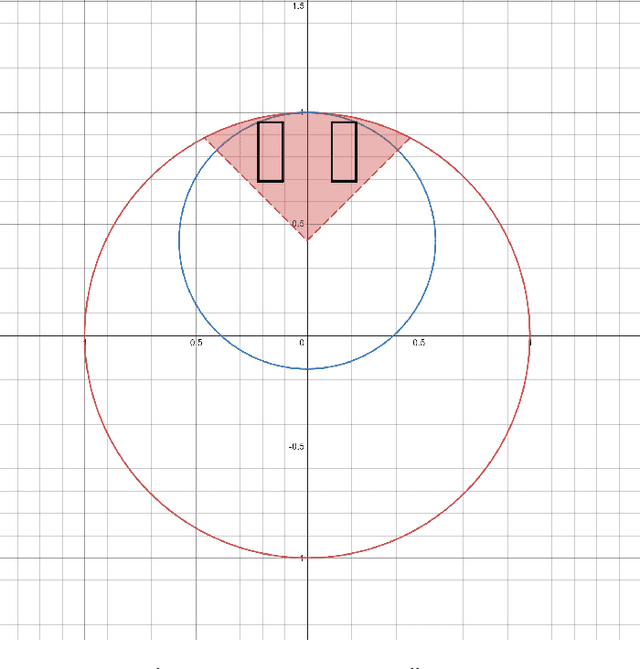
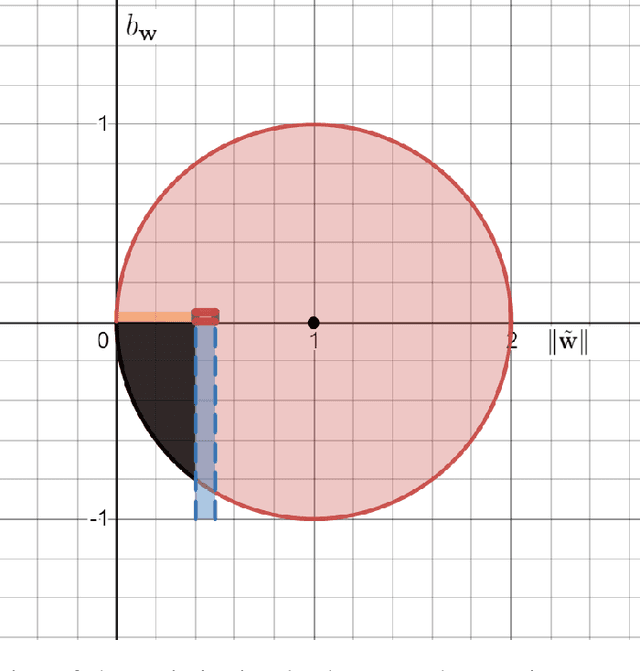
Learning a Single Neuron with Bias Using Gradient Descent

We theoretically study the fundamental problem of learning a single neuron with a bias term ($\mathbf{x} \mapsto \sigma(<\mathbf{w},\mathbf{x}> + b)$) in the realizable setting with the ReLU activation, using gradient descent. Perhaps surprisingly, we show that this is a significantly different and more challenging problem than the bias-less case (which was the focus of previous works on single neurons), both in terms of the optimization geometry as well as the ability of gradient methods to succeed in some scenarios. We provide a detailed study of this problem, characterizing the critical points of the objective, demonstrating failure cases, and providing positive convergence guarantees under different sets of assumptions. To prove our results, we develop some tools which may be of independent interest, and improve previous results on learning single neurons.