Fooling Algorithms in Non-Stationary Bandits using Belief Inertia

We study the problem of worst case regret in piecewise stationary multi armed bandits. While the minimax theory for stationary bandits is well established, understanding analogous limits in time-varying settings is challenging. Existing lower bounds rely on what we refer to as infrequent sampling arguments, where long intervals without exploration allow adversarial reward changes that induce large regret. In this paper, we introduce a fundamentally different approach based on a belief inertia argument. Our analysis captures how an algorithm's empirical beliefs, encoded through historical reward averages, create momentum that resists new evidence after a change. We show how this inertia can be exploited to construct adversarial instances that mislead classical algorithms such as Explore Then Commit, epsilon greedy, and UCB, causing them to suffer regret that grows linearly with T and with a substantial constant factor, regardless of how their parameters are tuned, even with a single change point. We extend the analysis to algorithms that periodically restart to handle non stationarity and prove that, even then, the worst case regret remains linear in T. Our results indicate that utilizing belief inertia can be a powerful method for deriving sharp lower bounds in non stationary bandits.

Communication-Efficient Federated Learning via Robust Distributed Mean Estimation

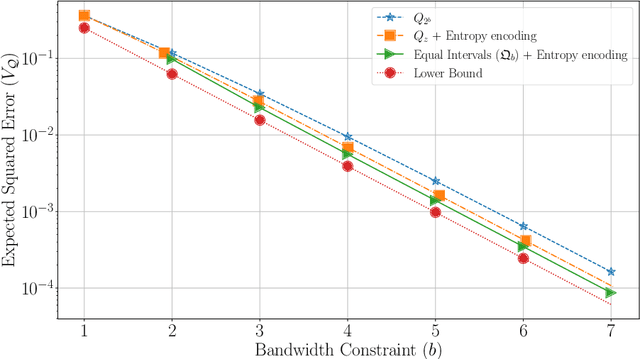
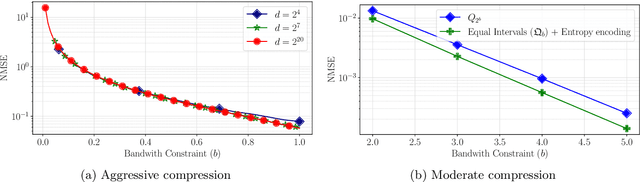
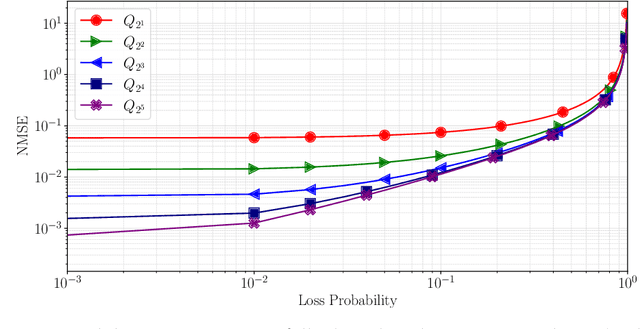
Federated learning commonly relies on algorithms such as distributed (mini-batch) SGD, where multiple clients compute their gradients and send them to a central coordinator for averaging and updating the model. To optimize the transmission time and the scalability of the training process, clients often use lossy compression to reduce the message sizes. DRIVE is a recent state of the art algorithm that compresses gradients using one bit per coordinate (with some lower-order overhead). In this technical report, we generalize DRIVE to support any bandwidth constraint as well as extend it to support heterogeneous client resources and make it robust to packet loss.

DRIVE: One-bit Distributed Mean Estimation

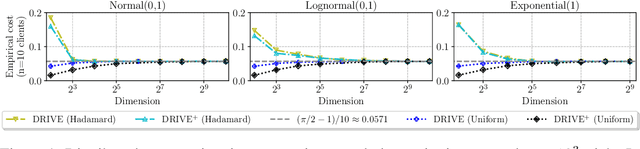
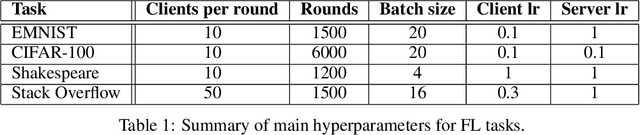
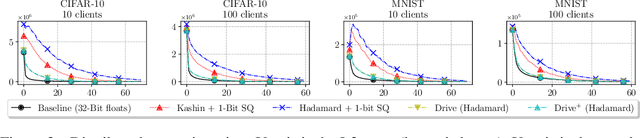
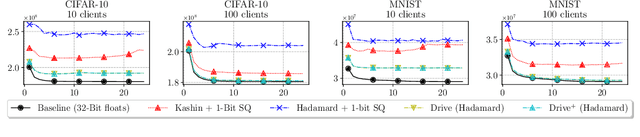
We consider the problem where $n$ clients transmit $d$-dimensional real-valued vectors using $d(1+o(1))$ bits each, in a manner that allows the receiver to approximately reconstruct their mean. Such compression problems naturally arise in distributed and federated learning. We provide novel mathematical results and derive computationally efficient algorithms that are more accurate than previous compression techniques. We evaluate our methods on a collection of distributed and federated learning tasks, using a variety of datasets, and show a consistent improvement over the state of the art.