Gabriel A. Silva
Quantifying Emergence in Neural Networks: Insights from Pruning and Training Dynamics
Sep 03, 2024Abstract:Emergence, where complex behaviors develop from the interactions of simpler components within a network, plays a crucial role in enhancing neural network capabilities. We introduce a quantitative framework to measure emergence during the training process and examine its impact on network performance, particularly in relation to pruning and training dynamics. Our hypothesis posits that the degree of emergence, defined by the connectivity between active and inactive nodes, can predict the development of emergent behaviors in the network. Through experiments with feedforward and convolutional architectures on benchmark datasets, we demonstrate that higher emergence correlates with improved trainability and performance. We further explore the relationship between network complexity and the loss landscape, suggesting that higher emergence indicates a greater concentration of local minima and a more rugged loss landscape. Pruning, which reduces network complexity by removing redundant nodes and connections, is shown to enhance training efficiency and convergence speed, though it may lead to a reduction in final accuracy. These findings provide new insights into the interplay between emergence, complexity, and performance in neural networks, offering valuable implications for the design and optimization of more efficient architectures.
Advancing Neural Network Performance through Emergence-Promoting Initialization Scheme
Jul 26, 2024Abstract:We introduce a novel yet straightforward neural network initialization scheme that modifies conventional methods like Xavier and Kaiming initialization. Inspired by the concept of emergence and leveraging the emergence measures proposed by Li (2023), our method adjusts the layer-wise weight scaling factors to achieve higher emergence values. This enhancement is easy to implement, requiring no additional optimization steps for initialization compared to GradInit. We evaluate our approach across various architectures, including MLP and convolutional architectures for image recognition, and transformers for machine translation. We demonstrate substantial improvements in both model accuracy and training speed, with and without batch normalization. The simplicity, theoretical innovation, and demonstrable empirical advantages of our method make it a potent enhancement to neural network initialization practices. These results suggest a promising direction for leveraging emergence to improve neural network training methodologies. Code is available at: https://github.com/johnnyjingzeli/EmergenceInit.
Using Quantum Computing to Infer Dynamic Behaviors of Biological and Artificial Neural Networks
Mar 27, 2024



Abstract:The exploration of new problem classes for quantum computation is an active area of research. An essentially completely unexplored topic is the use of quantum algorithms and computing to explore and ask questions \textit{about} the functional dynamics of neural networks. This is a component of the still-nascent topic of applying quantum computing to the modeling and simulations of biological and artificial neural networks. In this work, we show how a carefully constructed set of conditions can use two foundational quantum algorithms, Grover and Deutsch-Josza, in such a way that the output measurements admit an interpretation that guarantees we can infer if a simple representation of a neural network (which applies to both biological and artificial networks) after some period of time has the potential to continue sustaining dynamic activity. Or whether the dynamics are guaranteed to stop either through 'epileptic' dynamics or quiescence.
Learning without gradient descent encoded by the dynamics of a neurobiological model
Mar 23, 2021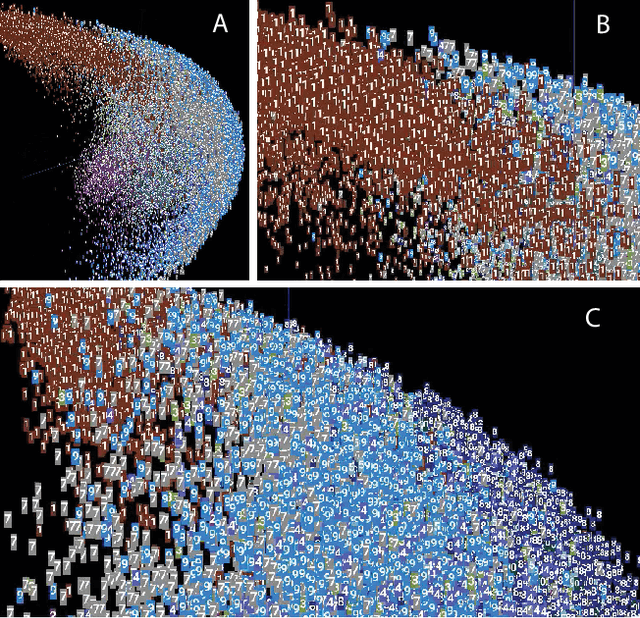
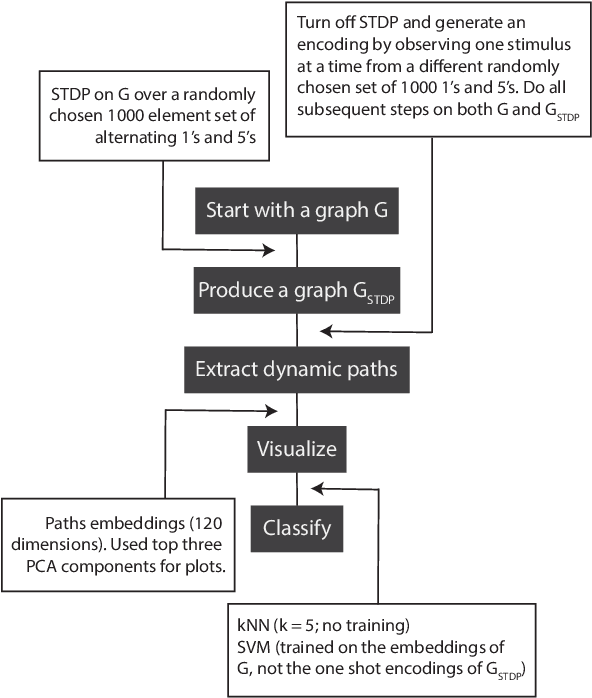
Abstract:The success of state-of-the-art machine learning is essentially all based on different variations of gradient descent algorithms that minimize some version of a cost or loss function. A fundamental limitation, however, is the need to train these systems in either supervised or unsupervised ways by exposing them to typically large numbers of training examples. Here, we introduce a fundamentally novel conceptual approach to machine learning that takes advantage of a neurobiologically derived model of dynamic signaling, constrained by the geometric structure of a network. We show that MNIST images can be uniquely encoded and classified by the dynamics of geometric networks with nearly state-of-the-art accuracy in an unsupervised way, and without the need for any training.
Generalizable Machine Learning in Neuroscience using Graph Neural Networks
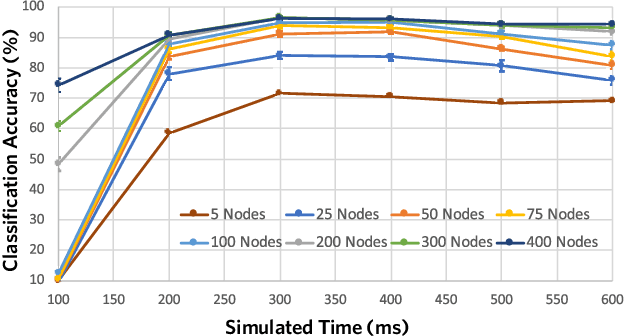
Oct 16, 2020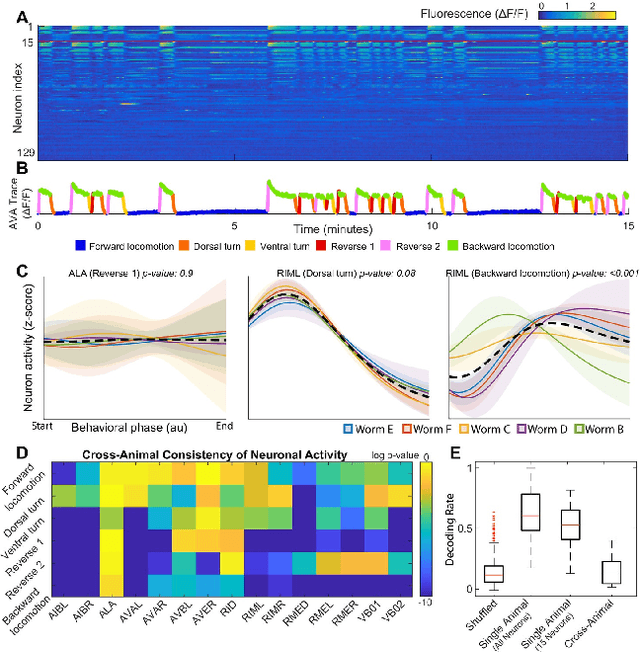
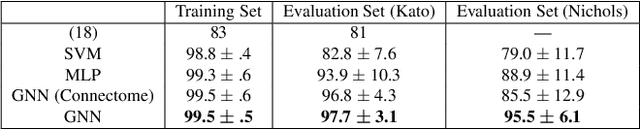
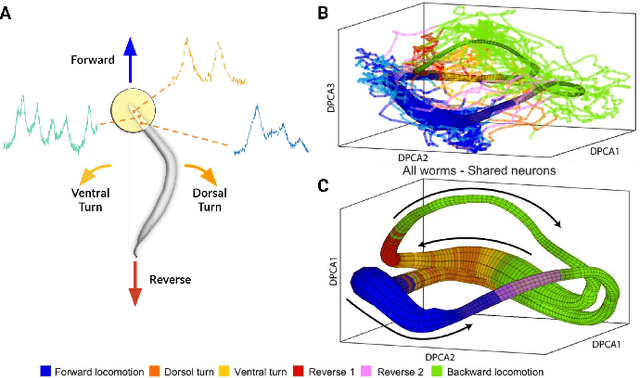
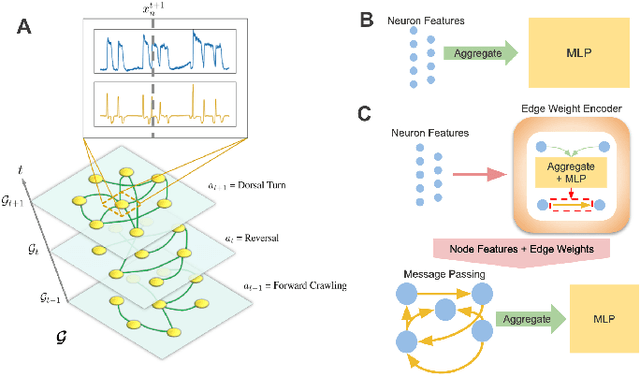
Abstract:Although a number of studies have explored deep learning in neuroscience, the application of these algorithms to neural systems on a microscopic scale, i.e. parameters relevant to lower scales of organization, remains relatively novel. Motivated by advances in whole-brain imaging, we examined the performance of deep learning models on microscopic neural dynamics and resulting emergent behaviors using calcium imaging data from the nematode C. elegans. We show that neural networks perform remarkably well on both neuron-level dynamics prediction, and behavioral state classification. In addition, we compared the performance of structure agnostic neural networks and graph neural networks to investigate if graph structure can be exploited as a favorable inductive bias. To perform this experiment, we designed a graph neural network which explicitly infers relations between neurons from neural activity and leverages the inferred graph structure during computations. In our experiments, we found that graph neural networks generally outperformed structure agnostic models and excel in generalization on unseen organisms, implying a potential path to generalizable machine learning in neuroscience.
Mapping the spatiotemporal dynamics of calcium signaling in cellular neural networks using optical flow
Jan 22, 2010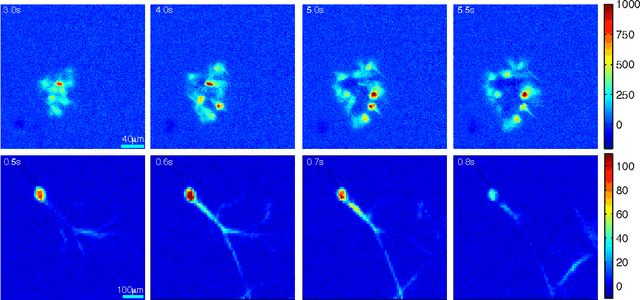
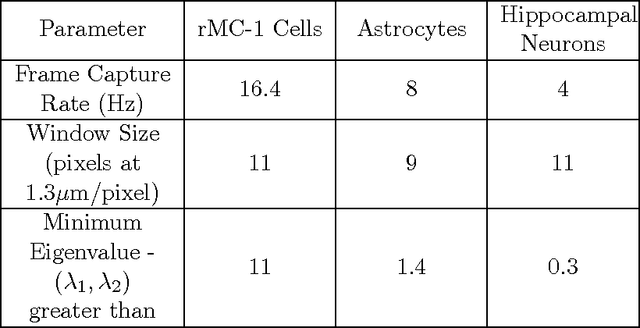


Abstract:An optical flow gradient algorithm was applied to spontaneously forming net- works of neurons and glia in culture imaged by fluorescence optical microscopy in order to map functional calcium signaling with single pixel resolution. Optical flow estimates the direction and speed of motion of objects in an image between subsequent frames in a recorded digital sequence of images (i.e. a movie). Computed vector field outputs by the algorithm were able to track the spatiotemporal dynamics of calcium signaling pat- terns. We begin by briefly reviewing the mathematics of the optical flow algorithm, and then describe how to solve for the displacement vectors and how to measure their reliability. We then compare computed flow vectors with manually estimated vectors for the progression of a calcium signal recorded from representative astrocyte cultures. Finally, we applied the algorithm to preparations of primary astrocytes and hippocampal neurons and to the rMC-1 Muller glial cell line in order to illustrate the capability of the algorithm for capturing different types of spatiotemporal calcium activity. We discuss the imaging requirements, parameter selection and threshold selection for reliable measurements, and offer perspectives on uses of the vector data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge