Franz Pernkopf
Graz University of Technology
Resource-Efficient Neural Networks for Embedded Systems
Jan 07, 2020
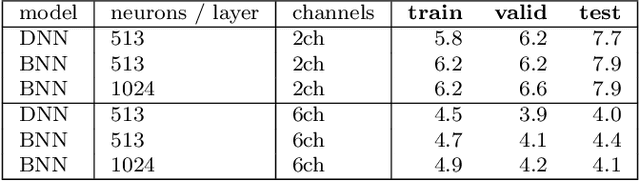
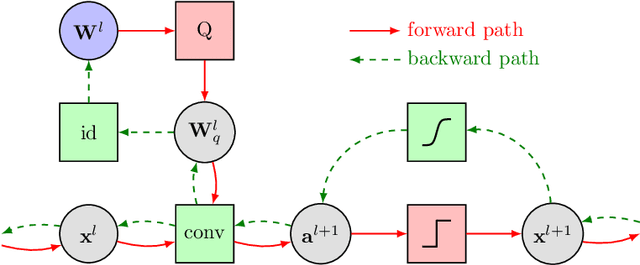
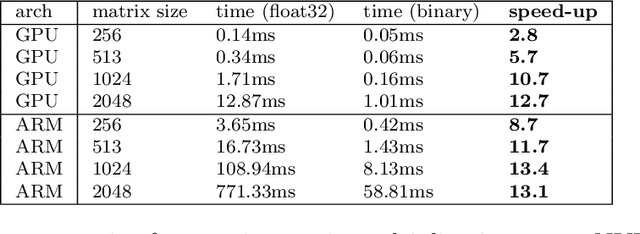
Abstract:While machine learning is traditionally a resource intensive task, embedded systems, autonomous navigation, and the vision of the Internet of Things fuel the interest in resource-efficient approaches. These approaches aim for a carefully chosen trade-off between performance and resource consumption in terms of computation and energy. The development of such approaches is among the major challenges in current machine learning research and key to ensure a smooth transition of machine learning technology from a scientific environment with virtually unlimited computing resources into every day's applications. In this article, we provide an overview of the current state of the art of machine learning techniques facilitating these real-world requirements. In particular, we focus on deep neural networks (DNNs), the predominant machine learning models of the past decade. We give a comprehensive overview of the vast literature that can be mainly split into three non-mutually exclusive categories: (i) quantized neural networks, (ii) network pruning, and (iii) structural efficiency. These techniques can be applied during training or as post-processing, and they are widely used to reduce the computational demands in terms of memory footprint, inference speed, and energy efficiency. We substantiate our discussion with experiments on well-known benchmark data sets to showcase the difficulty of finding good trade-offs between resource-efficiency and predictive performance.
Deep Structured Mixtures of Gaussian Processes
Oct 10, 2019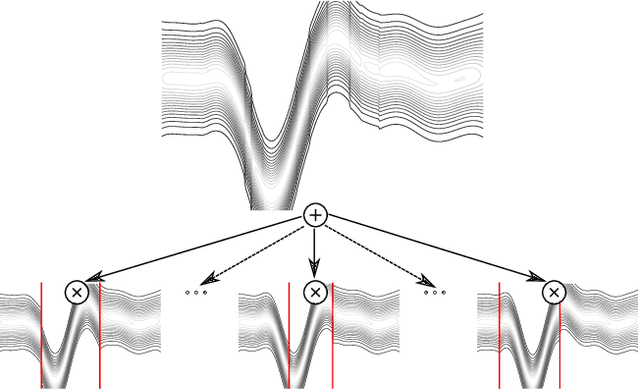
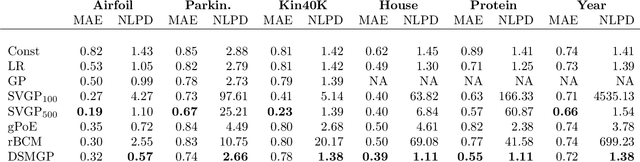
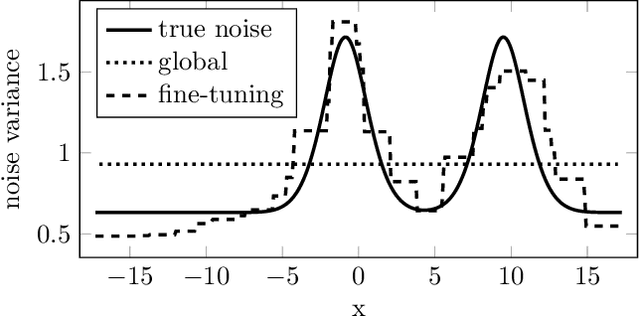
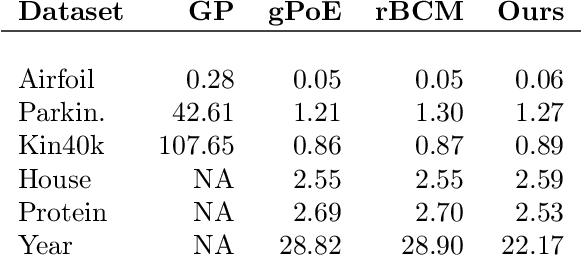
Abstract:Gaussian Processes (GPs) are powerful non-parametric Bayesian regression models that allow exact posterior inference, but exhibit high computational and memory costs. In order to improve scalability of GPs, approximate posterior inference is frequently employed, where a prominent class of approximation techniques is based on local GP experts. However, the local-expert techniques proposed so far are either not well-principled, come with limited approximation guarantees, or lead to intractable models. In this paper, we introduce deep structured mixtures of GP experts, a stochastic process model which i) allows exact posterior inference, ii) has attractive computational and memory costs, and iii), when used as GP approximation, captures predictive uncertainties consistently better than previous approximations. In a variety of experiments, we show that deep structured mixtures have a low approximation error and outperform existing expert-based approaches.
Learning a Behavior Model of Hybrid Systems Through Combining Model-Based Testing and Machine Learning
Jul 10, 2019
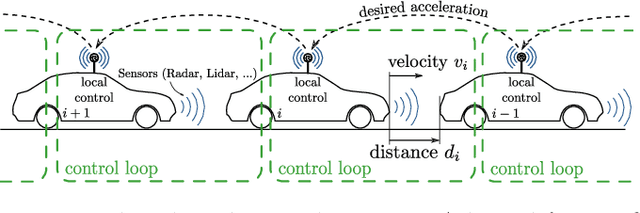
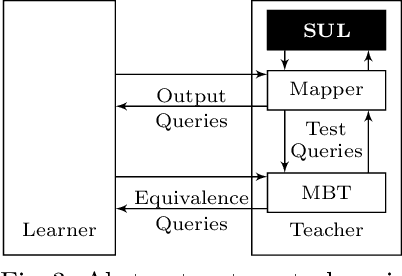
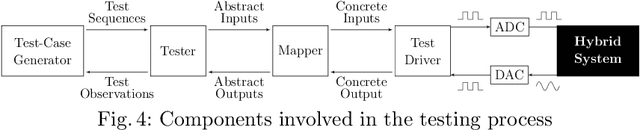
Abstract:Models play an essential role in the design process of cyber-physical systems. They form the basis for simulation and analysis and help in identifying design problems as early as possible. However, the construction of models that comprise physical and digital behavior is challenging. Therefore, there is considerable interest in learning such hybrid behavior by means of machine learning which requires sufficient and representative training data covering the behavior of the physical system adequately. In this work, we exploit a combination of automata learning and model-based testing to generate sufficient training data fully automatically. Experimental results on a platooning scenario show that recurrent neural networks learned with this data achieved significantly better results compared to models learned from randomly generated data. In particular, the classification error for crash detection is reduced by a factor of five and a similar F1-score is obtained with up to three orders of magnitude fewer training samples.
Complex Signal Denoising and Interference Mitigation for Automotive Radar Using Convolutional Neural Networks
Jun 25, 2019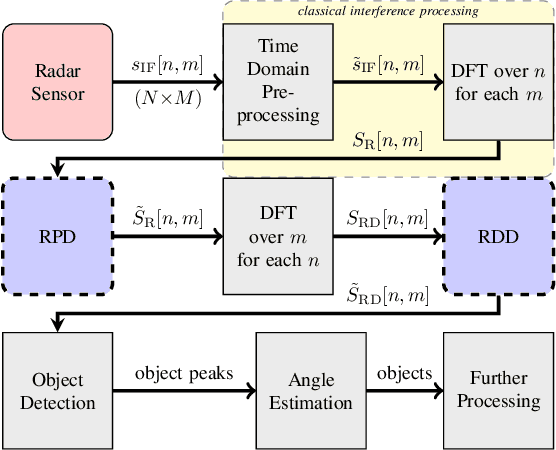
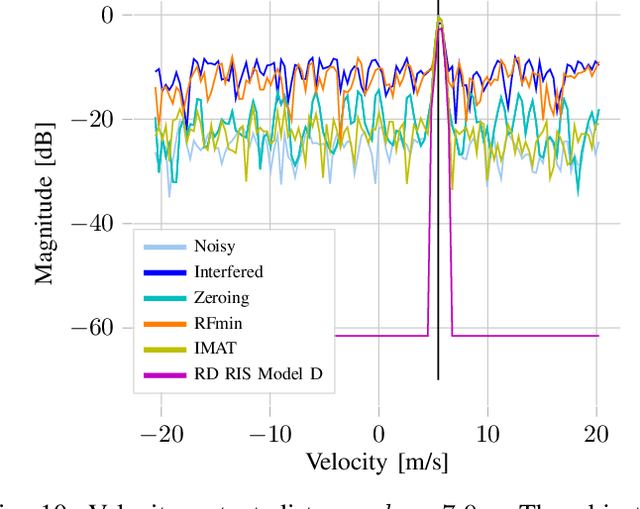
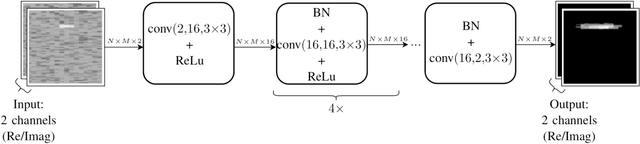
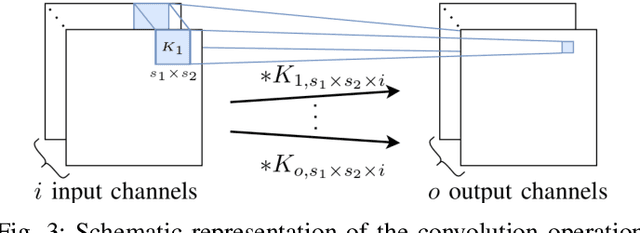
Abstract:Driver assistance systems as well as autonomous cars have to rely on sensors to perceive their environment. A heterogeneous set of sensors is used to perform this task robustly. Among them, radar sensors are indispensable because of their range resolution and the possibility to directly measure velocity. Since more and more radar sensors are deployed on the streets, mutual interference must be dealt with. In the so far unregulated automotive radar frequency band, a sensor must be capable of detecting, or even mitigating the harmful effects of interference, which include a decreased detection sensitivity. In this paper, we address this issue with Convolutional Neural Networks (CNNs), which are state-of-the-art machine learning tools. We show that the ability of CNNs to find structured information in data while preserving local information enables superior denoising performance. To achieve this, CNN parameters are found using training with simulated data and integrated into the automotive radar signal processing chain. The presented method is compared with the state of the art, highlighting its promising performance. Hence, CNNs can be employed for interference mitigation as an alternative to conventional signal processing methods. Code and pre-trained models are available at https://github.com/johanna-rock/imRICnn.
Parameterized Structured Pruning for Deep Neural Networks
Jun 12, 2019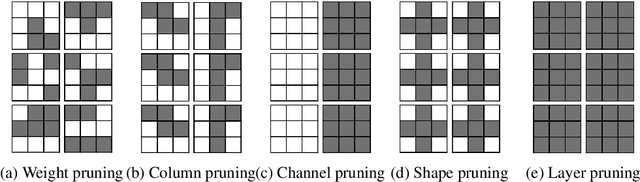

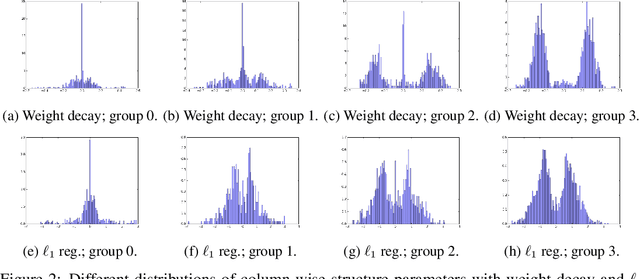
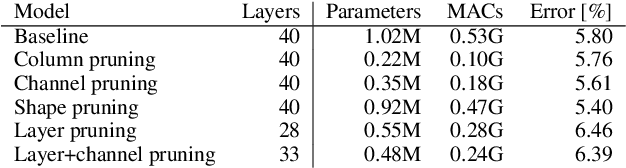
Abstract:As a result of the growing size of Deep Neural Networks (DNNs), the gap to hardware capabilities in terms of memory and compute increases. To effectively compress DNNs, quantization and connection pruning are usually considered. However, unconstrained pruning usually leads to unstructured parallelism, which maps poorly to massively parallel processors, and substantially reduces the efficiency of general-purpose processors. Similar applies to quantization, which often requires dedicated hardware. We propose Parameterized Structured Pruning (PSP), a novel method to dynamically learn the shape of DNNs through structured sparsity. PSP parameterizes structures (e.g. channel- or layer-wise) in a weight tensor and leverages weight decay to learn a clear distinction between important and unimportant structures. As a result, PSP maintains prediction performance, creates a substantial amount of sparsity that is structured and, thus, easy and efficient to map to a variety of massively parallel processors, which are mandatory for utmost compute power and energy efficiency. PSP is experimentally validated on the popular CIFAR10/100 and ILSVRC2012 datasets using ResNet and DenseNet architectures, respectively.
Optimisation of Overparametrized Sum-Product Networks
May 29, 2019
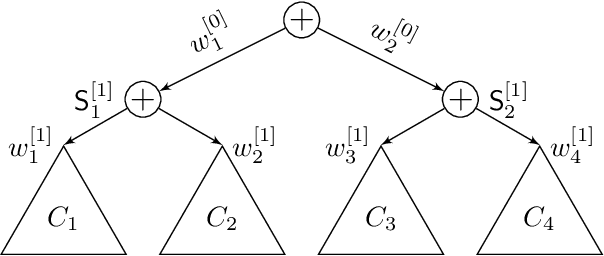
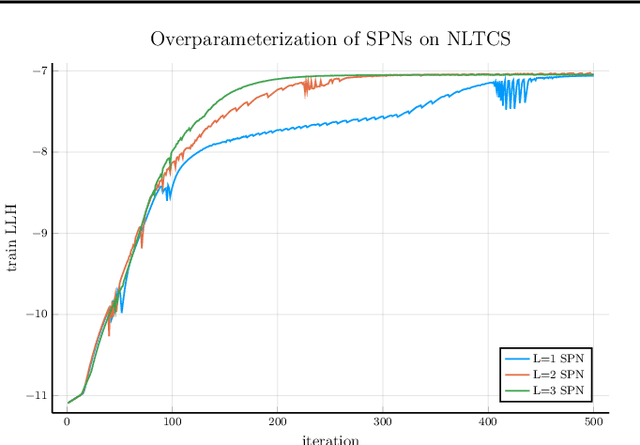
Abstract:It seems to be a pearl of conventional wisdom that parameter learning in deep sum-product networks is surprisingly fast compared to shallow mixture models. This paper examines the effects of overparameterization in sum-product networks on the speed of parameter optimisation. Using theoretical analysis and empirical experiments, we show that deep sum-product networks exhibit an implicit acceleration compared to their shallow counterpart. In fact, gradient-based optimisation in deep tree-structured sum-product networks is equal to gradient ascend with adaptive and time-varying learning rates and additional momentum terms.
Bayesian Learning of Sum-Product Networks
May 26, 2019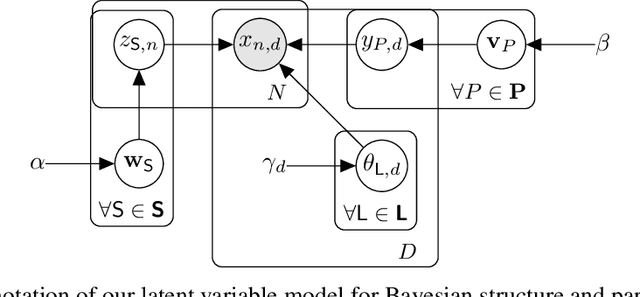
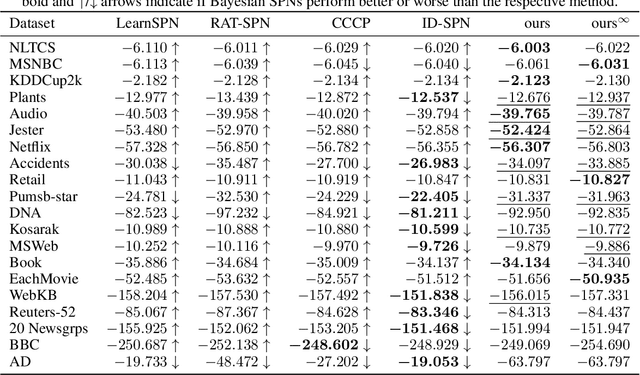
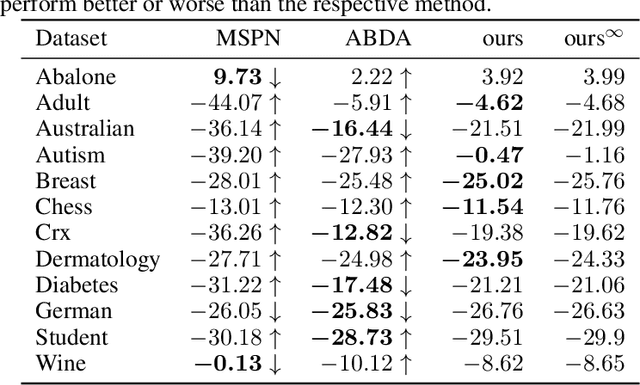
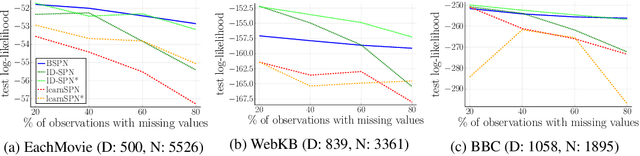
Abstract:Sum-product networks (SPNs) are flexible density estimators and have received significant attention, due to their attractive inference properties. While parameter learning in SPNs is well developed, structure learning leaves something to be desired: Even though there is a plethora of SPN structure learners, most of them are somewhat ad-hoc, and based on intuition rather than a clear learning principle. In this paper, we introduce a well-principled Bayesian framework for SPN structure learning. First, we decompose the problem into i) laying out a basic computational graph, and ii) learning the so-called scope function over the graph. The first is rather unproblematic and akin to neural network architecture validation. The second characterises the effective structure of the SPN and needs to respect the usual structural constraints in SPN, i.e. completeness and decomposability. While representing and learning the scope function is rather involved in general, in this paper, we propose a natural parametrisation for an important and widely used special case of SPNs. These structural parameters are incorporated into a Bayesian model, such that simultaneous structure and parameter learning is cast into monolithic Bayesian posterior inference. In various experiments, our Bayesian SPNs often improve test likelihoods over greedy SPN learners. Further, since the Bayesian framework protects against overfitting, we are able to evaluate hyper-parameters directly on the Bayesian model score, waiving the need for a separate validation set, which is especially beneficial in low data regimes. Bayesian SPNs can be applied to heterogeneous domains and can easily be extended to nonparametric formulations. Moreover, our Bayesian approach is the first which consistently and robustly learns SPN structures under missing data.
Efficient and Robust Machine Learning for Real-World Systems
Dec 05, 2018
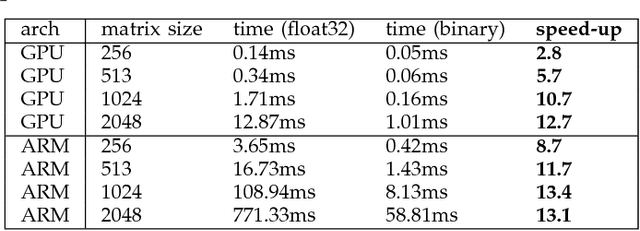
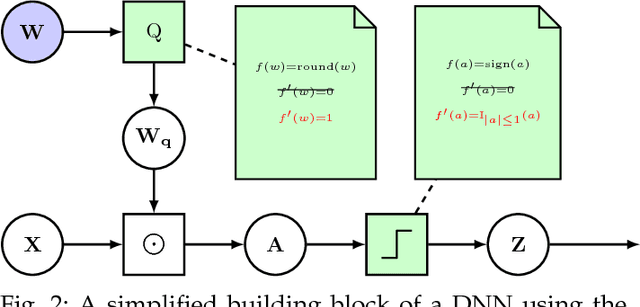
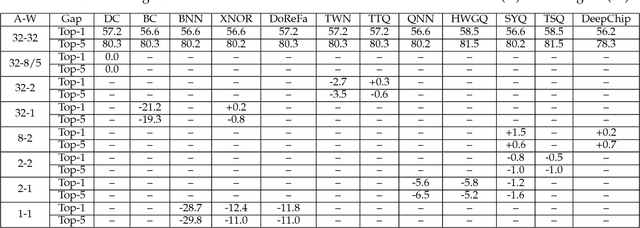
Abstract:While machine learning is traditionally a resource intensive task, embedded systems, autonomous navigation and the vision of the Internet-of-Things fuel the interest in resource efficient approaches. These approaches require a carefully chosen trade-off between performance and resource consumption in terms of computation and energy. On top of this, it is crucial to treat uncertainty in a consistent manner in all but the simplest applications of machine learning systems. In particular, a desideratum for any real-world system is to be robust in the presence of outliers and corrupted data, as well as being `aware' of its limits, i.e.\ the system should maintain and provide an uncertainty estimate over its own predictions. These complex demands are among the major challenges in current machine learning research and key to ensure a smooth transition of machine learning technology into every day's applications. In this article, we provide an overview of the current state of the art of machine learning techniques facilitating these real-world requirements. First we provide a comprehensive review of resource-efficiency in deep neural networks with focus on techniques for model size reduction, compression and reduced precision. These techniques can be applied during training or as post-processing and are widely used to reduce both computational complexity and memory footprint. As most (practical) neural networks are limited in their ways to treat uncertainty, we contrast them with probabilistic graphical models, which readily serve these desiderata by means of probabilistic inference. In that way, we provide an extensive overview of the current state-of-the-art of robust and efficient machine learning for real-world systems.
Self-Guided Belief Propagation -- A Homotopy Continuation Method
Dec 04, 2018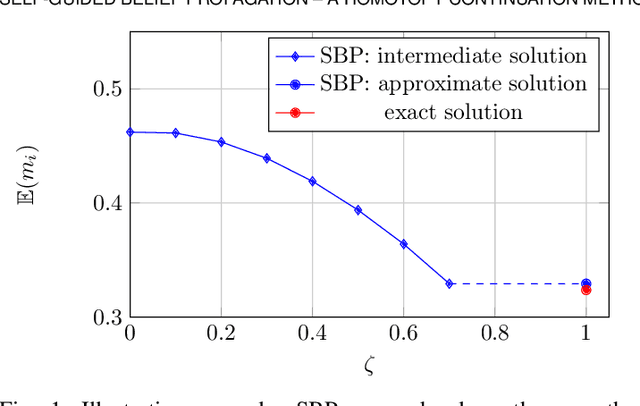
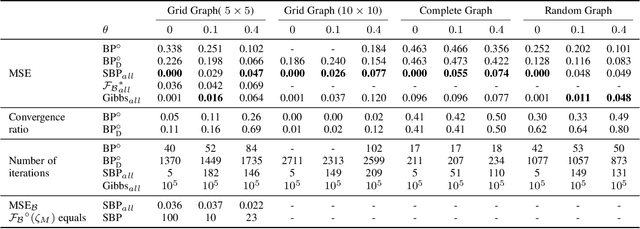
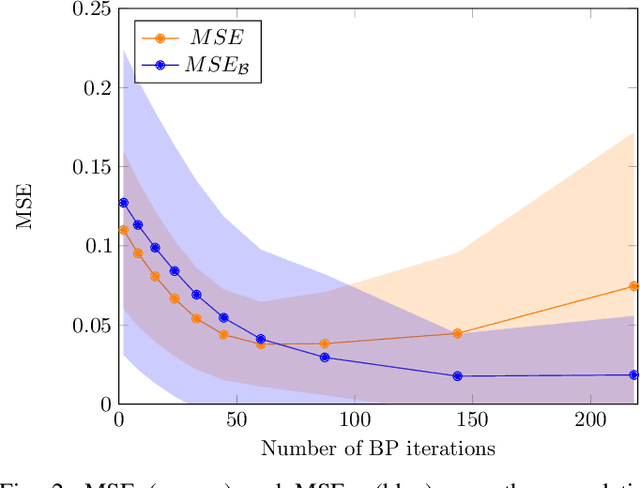
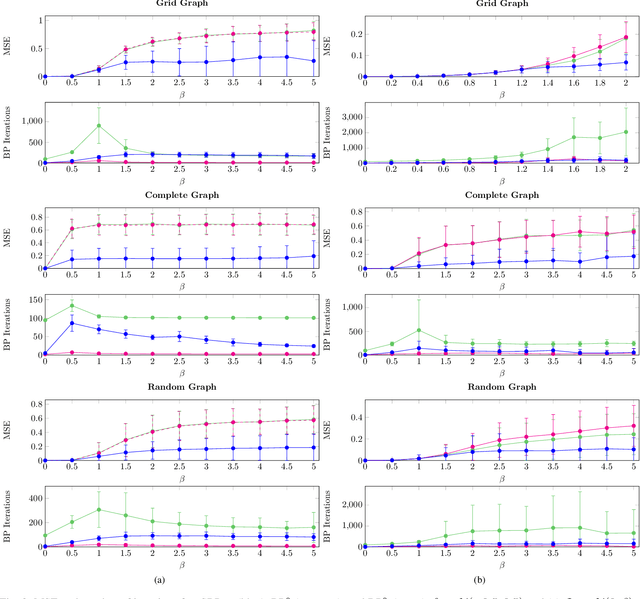
Abstract:We propose self-guided belief propagation (SBP) that modifies belief propagation (BP) by incorporating the pairwise potentials only gradually. This homotopy continuation method converges to a unique solution and increases the accuracy without increasing the computational burden. We apply SBP to grid graphs, complete graphs, and random graphs with random Ising potentials and show that: (i) SBP is superior in terms of accuracy whenever BP converges, and (ii) SBP obtains a unique, stable, and accurate solution whenever BP does not converge. We further provide a formal analysis to demonstrate that SBP obtains the global optimum of the Bethe approximation for attractive models with unidirectional fields.
Learning Deep Mixtures of Gaussian Process Experts Using Sum-Product Networks
Sep 12, 2018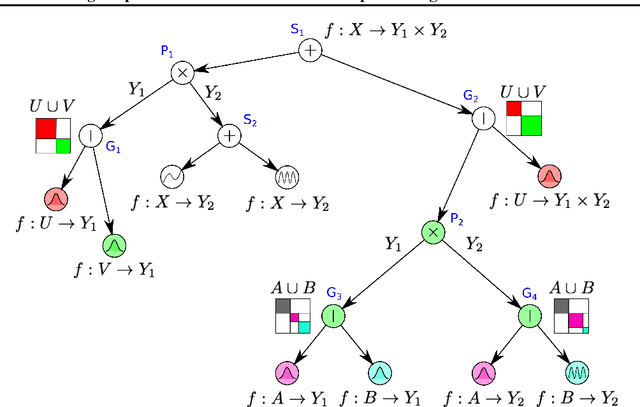
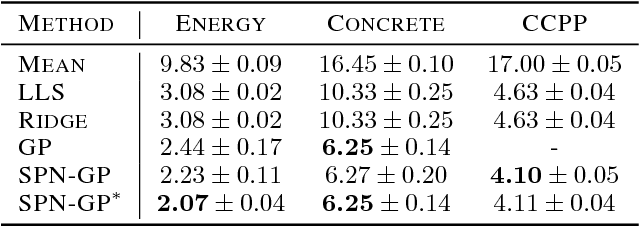
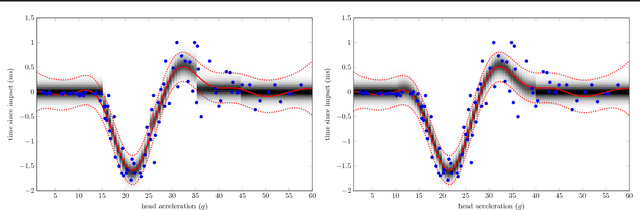
Abstract:While Gaussian processes (GPs) are the method of choice for regression tasks, they also come with practical difficulties, as inference cost scales cubic in time and quadratic in memory. In this paper, we introduce a natural and expressive way to tackle these problems, by incorporating GPs in sum-product networks (SPNs), a recently proposed tractable probabilistic model allowing exact and efficient inference. In particular, by using GPs as leaves of an SPN we obtain a novel flexible prior over functions, which implicitly represents an exponentially large mixture of local GPs. Exact and efficient posterior inference in this model can be done in a natural interplay of the inference mechanisms in GPs and SPNs. Thereby, each GP is -- similarly as in a mixture of experts approach -- responsible only for a subset of data points, which effectively reduces inference cost in a divide and conquer fashion. We show that integrating GPs into the SPN framework leads to a promising probabilistic regression model which is: (1) computational and memory efficient, (2) allows efficient and exact posterior inference, (3) is flexible enough to mix different kernel functions, and (4) naturally accounts for non-stationarities in time series. In a variate of experiments, we show that the SPN-GP model can learn input dependent parameters and hyper-parameters and is on par with or outperforms the traditional GPs as well as state of the art approximations on real-world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge