Gradient-free optimization of chaotic acoustics with reservoir computing

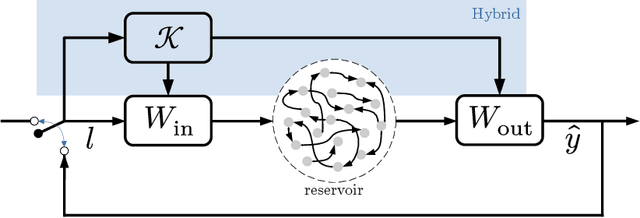
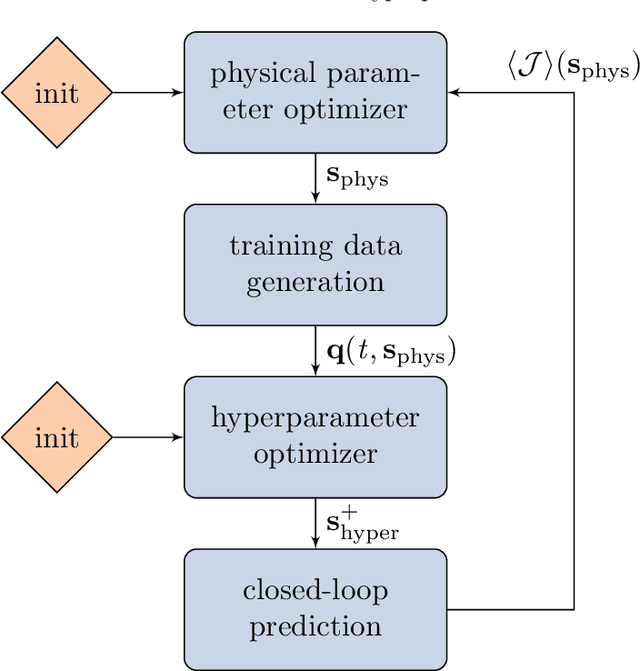
We develop a versatile optimization method, which finds the design parameters that minimize time-averaged acoustic cost functionals. The method is gradient-free, model-informed, and data-driven with reservoir computing based on echo state networks. First, we analyse the predictive capabilities of echo state networks both in the short- and long-time prediction of the dynamics. We find that both fully data-driven and model-informed architectures learn the chaotic acoustic dynamics, both time-accurately and statistically. Informing the training with a physical reduced-order model with one acoustic mode markedly improves the accuracy and robustness of the echo state networks, whilst keeping the computational cost low. Echo state networks offer accurate predictions of the long-time dynamics, which would be otherwise expensive by integrating the governing equations to evaluate the time-averaged quantity to optimize. Second, we couple echo state networks with a Bayesian technique to explore the design thermoacoustic parameter space. The computational method is minimally intrusive. Third, we find the set of flame parameters that minimize the time-averaged acoustic energy of chaotic oscillations, which are caused by the positive feedback with a heat source, such as a flame in gas turbines or rocket motors. These oscillations are known as thermoacoustic oscillations. The optimal set of flame parameters is found with the same accuracy as brute-force grid search, but with a convergence rate that is more than one order of magnitude faster. This work opens up new possibilities for non-intrusive (``hands-off'') optimization of chaotic systems, in which the cost of generating data, for example from high-fidelity simulations and experiments, is high.

Learning ergodic averages in chaotic systems

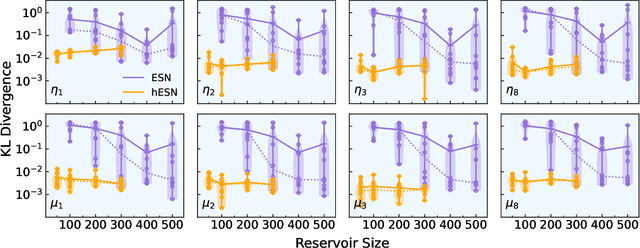
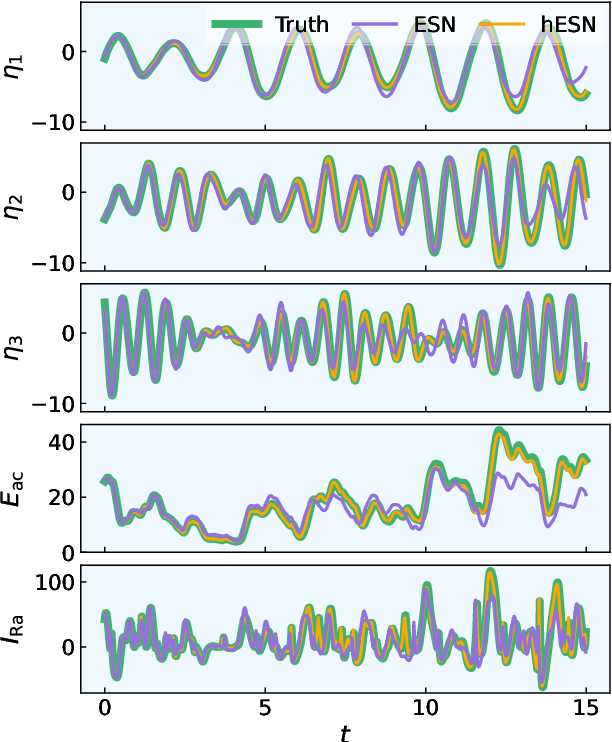
We propose a physics-informed machine learning method to predict the time average of a chaotic attractor. The method is based on the hybrid echo state network (hESN). We assume that the system is ergodic, so the time average is equal to the ergodic average. Compared to conventional echo state networks (ESN) (purely data-driven), the hESN uses additional information from an incomplete, or imperfect, physical model. We evaluate the performance of the hESN and compare it to that of an ESN. This approach is demonstrated on a chaotic time-delayed thermoacoustic system, where the inclusion of a physical model significantly improves the accuracy of the prediction, reducing the relative error from 48% to 7%. This improvement is obtained at the low extra cost of solving two ordinary differential equations. This framework shows the potential of using machine learning techniques combined with prior physical knowledge to improve the prediction of time-averaged quantities in chaotic systems.