Acceleration of Descent-based Optimization Algorithms via Carathéodory's Theorem

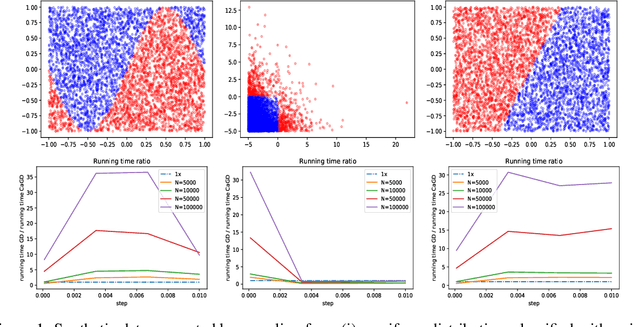
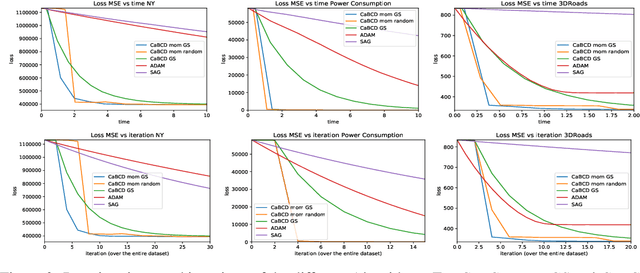
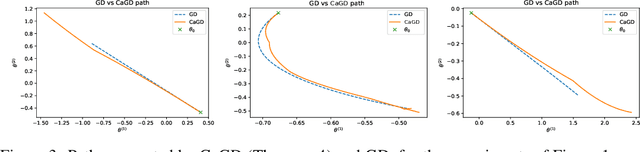
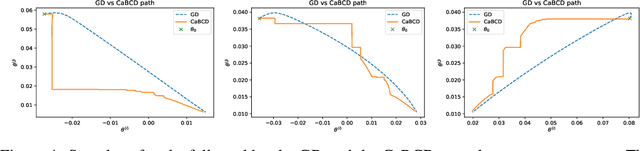
We propose a new technique to accelerate algorithms based on Gradient Descent using Carath\'eodory's Theorem. In the case of the standard Gradient Descent algorithm, we analyse the theoretical convergence of the approach under convexity assumptions and empirically display its ameliorations. As a core contribution, we then present an application of the acceleration technique to Block Coordinate Descent methods. Experimental comparisons on least squares regression with a LASSO regularisation term show remarkably improved performance on LASSO than the ADAM and SAG algorithms.

A Randomized Algorithm to Reduce the Support of Discrete Measures

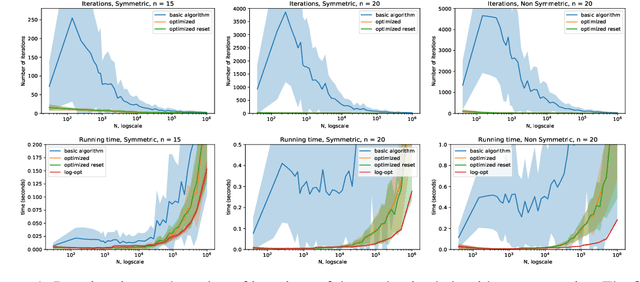
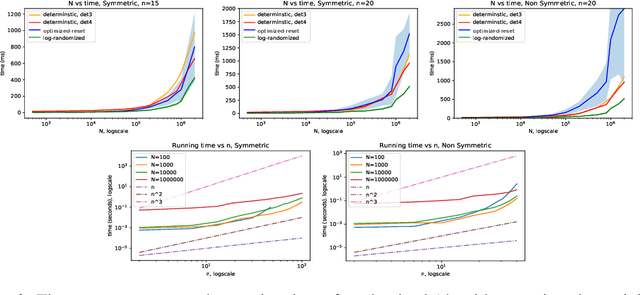
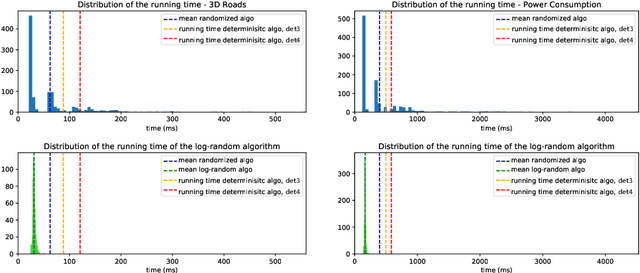
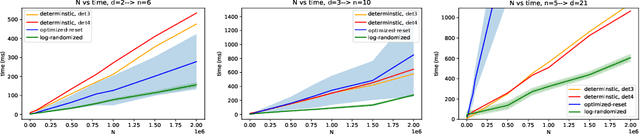
Given a discrete probability measure supported on $N$ atoms and a set of $n$ real-valued functions, there exists a probability measure that is supported on a subset of $n+1$ of the original $N$ atoms and has the same mean when integrated against each of the $n$ functions. If $ N \gg n$ this results in a huge reduction of complexity. We give a simple geometric characterization of barycenters via negative cones and derive a randomized algorithm that computes this new measure by ``greedy geometric sampling''. We then study its properties, and benchmark it on synthetic and real-world data to show that it can be very beneficial in the $N\gg n$ regime.