Squeezing More from the Stream : Learning Representation Online for Streaming Reinforcement Learning

In streaming Reinforcement Learning (RL), transitions are observed and discarded immediately after a single update. While this minimizes resource usage for on-device applications, it makes agents notoriously sample-inefficient, since value-based losses alone struggle to extract meaningful representations from transient data. We propose extending Self-Predictive Representations (SPR) to the streaming pipeline to maximize the utility of every observed frame. However, due to the highly correlated samples induced by the streaming regime, naively applying this auxiliary loss results in training instabilities. Thus, we introduce orthogonal gradient updates relative to the momentum target and resolve gradient conflicts arising from streaming-specific optimizers. Validated across the Atari, MinAtar, and Octax suites, our approach systematically outperforms existing streaming baselines. Latent-space analysis, including t-SNE visualizations and effective-rank measurements, confirms that our method learns significantly richer representations, bridging the performance gap caused by the absence of a replay buffer, while remaining efficient enough to train on just a few CPU cores.

Parity Requires Unified Input Dependence and Negative Eigenvalues in SSMs

Recent work has shown that LRNN models such as S4D, Mamba, and DeltaNet lack state-tracking capability due to either time-invariant transition matrices or restricted eigenvalue ranges. To address this, input-dependent transition matrices, particularly those that are complex or non-triangular, have been proposed to enhance SSM performance on such tasks. While existing theorems demonstrate that both input-independent and non-negative SSMs are incapable of solving simple state-tracking tasks, such as parity, regardless of depth, they do not explore whether combining these two types in a multilayer SSM could help. We investigate this question for efficient SSMs with diagonal transition matrices and show that such combinations still fail to solve parity. This implies that a recurrence layer must both be input-dependent and include negative eigenvalues. Our experiments support this conclusion by analyzing an SSM model that combines S4D and Mamba layers.

ChronosPerseus: Randomized Point-based Value Iteration with Importance Sampling for POSMDPs

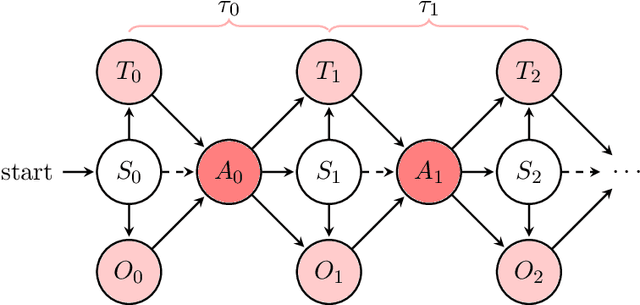
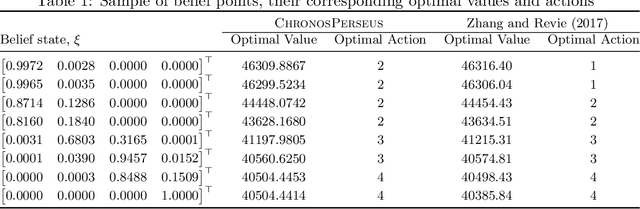
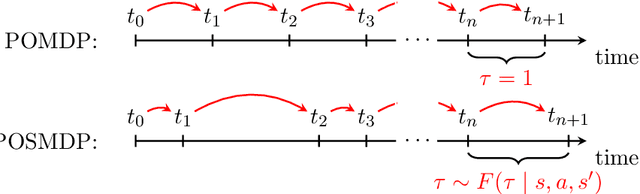
In reinforcement learning, agents have successfully used environments modeled with Markov decision processes (MDPs). However, in many problem domains, an agent may suffer from noisy observations or random times until its subsequent decision. While partially observable Markov decision processes (POMDPs) have dealt with noisy observations, they have yet to deal with the unknown time aspect. Of course, one could discretize the time, but this leads to Bellman's Curse of Dimensionality. To incorporate continuous sojourn-time distributions in the agent's decision making, we propose that partially observable semi-Markov decision processes (POSMDPs) can be helpful in this regard. We extend \citet{Spaan2005a} randomized point-based value iteration (PBVI) \textsc{Perseus} algorithm used for POMDP to POSMDP by incorporating continuous sojourn time distributions and using importance sampling to reduce the solver complexity. We call this new PBVI algorithm with importance sampling for POSMDPs -- \textsc{ChronosPerseus}. This further allows for compressed complex POMDPs requiring temporal state information by moving this information into state sojourn time of a POMSDP. The second insight is that keeping a set of sampled times and weighting it by its likelihood can be used in a single backup; this helps further reduce the algorithm complexity. The solver also works on episodic and non-episodic problems. We conclude our paper with two examples, an episodic bus problem and a non-episodic maintenance problem.