Fakhri Karray
Arabic Dysarthric Speech Recognition Using Adversarial and Signal-Based Augmentation
Jun 07, 2023



Abstract:Despite major advancements in Automatic Speech Recognition (ASR), the state-of-the-art ASR systems struggle to deal with impaired speech even with high-resource languages. In Arabic, this challenge gets amplified, with added complexities in collecting data from dysarthric speakers. In this paper, we aim to improve the performance of Arabic dysarthric automatic speech recognition through a multi-stage augmentation approach. To this effect, we first propose a signal-based approach to generate dysarthric Arabic speech from healthy Arabic speech by modifying its speed and tempo. We also propose a second stage Parallel Wave Generative (PWG) adversarial model that is trained on an English dysarthric dataset to capture language-independant dysarthric speech patterns and further augment the signal-adjusted speech samples. Furthermore, we propose a fine-tuning and text-correction strategies for Arabic Conformer at different dysarthric speech severity levels. Our fine-tuned Conformer achieved 18% Word Error Rate (WER) and 17.2% Character Error Rate (CER) on synthetically generated dysarthric speech from the Arabic commonvoice speech dataset. This shows significant WER improvement of 81.8% compared to the baseline model trained solely on healthy data. We perform further validation on real English dysarthric speech showing a WER improvement of 124% compared to the baseline trained only on healthy English LJSpeech dataset.
Clip21: Error Feedback for Gradient Clipping
May 30, 2023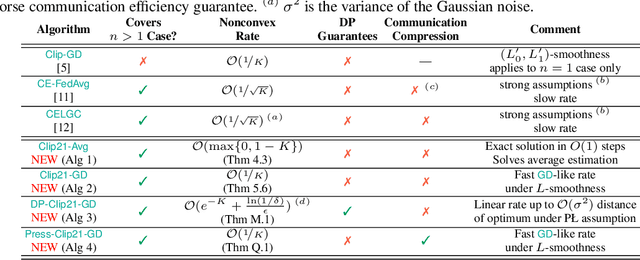
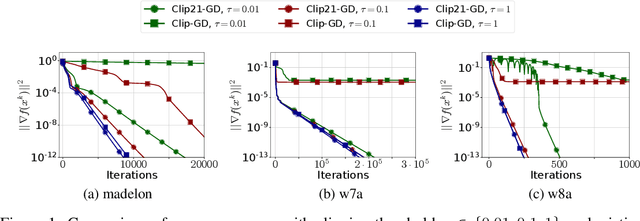
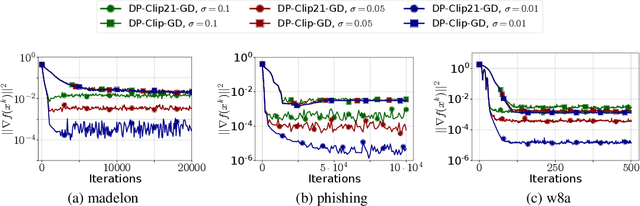
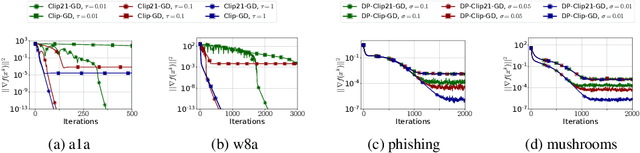
Abstract:Motivated by the increasing popularity and importance of large-scale training under differential privacy (DP) constraints, we study distributed gradient methods with gradient clipping, i.e., clipping applied to the gradients computed from local information at the nodes. While gradient clipping is an essential tool for injecting formal DP guarantees into gradient-based methods [1], it also induces bias which causes serious convergence issues specific to the distributed setting. Inspired by recent progress in the error-feedback literature which is focused on taming the bias/error introduced by communication compression operators such as Top-$k$ [2], and mathematical similarities between the clipping operator and contractive compression operators, we design Clip21 -- the first provably effective and practically useful error feedback mechanism for distributed methods with gradient clipping. We prove that our method converges at the same $\mathcal{O}\left(\frac{1}{K}\right)$ rate as distributed gradient descent in the smooth nonconvex regime, which improves the previous best $\mathcal{O}\left(\frac{1}{\sqrt{K}}\right)$ rate which was obtained under significantly stronger assumptions. Our method converges significantly faster in practice than competing methods.
Multi-Plane Neural Radiance Fields for Novel View Synthesis
Mar 03, 2023Abstract:Novel view synthesis is a long-standing problem that revolves around rendering frames of scenes from novel camera viewpoints. Volumetric approaches provide a solution for modeling occlusions through the explicit 3D representation of the camera frustum. Multi-plane Images (MPI) are volumetric methods that represent the scene using front-parallel planes at distinct depths but suffer from depth discretization leading to a 2.D scene representation. Another line of approach relies on implicit 3D scene representations. Neural Radiance Fields (NeRF) utilize neural networks for encapsulating the continuous 3D scene structure within the network weights achieving photorealistic synthesis results, however, methods are constrained to per-scene optimization settings which are inefficient in practice. Multi-plane Neural Radiance Fields (MINE) open the door for combining implicit and explicit scene representations. It enables continuous 3D scene representations, especially in the depth dimension, while utilizing the input image features to avoid per-scene optimization. The main drawback of the current literature work in this domain is being constrained to single-view input, limiting the synthesis ability to narrow viewpoint ranges. In this work, we thoroughly examine the performance, generalization, and efficiency of single-view multi-plane neural radiance fields. In addition, we propose a new multiplane NeRF architecture that accepts multiple views to improve the synthesis results and expand the viewing range. Features from the input source frames are effectively fused through a proposed attention-aware fusion module to highlight important information from different viewpoints. Experiments show the effectiveness of attention-based fusion and the promising outcomes of our proposed method when compared to multi-view NeRF and MPI techniques.
Harris Hawks Feature Selection in Distributed Machine Learning for Secure IoT Environments
Feb 20, 2023



Abstract:The development of the Internet of Things (IoT) has dramatically expanded our daily lives, playing a pivotal role in the enablement of smart cities, healthcare, and buildings. Emerging technologies, such as IoT, seek to improve the quality of service in cognitive cities. Although IoT applications are helpful in smart building applications, they present a real risk as the large number of interconnected devices in those buildings, using heterogeneous networks, increases the number of potential IoT attacks. IoT applications can collect and transfer sensitive data. Therefore, it is necessary to develop new methods to detect hacked IoT devices. This paper proposes a Feature Selection (FS) model based on Harris Hawks Optimization (HHO) and Random Weight Network (RWN) to detect IoT botnet attacks launched from compromised IoT devices. Distributed Machine Learning (DML) aims to train models locally on edge devices without sharing data to a central server. Therefore, we apply the proposed approach using centralized and distributed ML models. Both learning models are evaluated under two benchmark datasets for IoT botnet attacks and compared with other well-known classification techniques using different evaluation indicators. The experimental results show an improvement in terms of accuracy, precision, recall, and F-measure in most cases. The proposed method achieves an average F-measure up to 99.9\%. The results show that the DML model achieves competitive performance against centralized ML while maintaining the data locally.
Integrating Digital Twin and Advanced Intelligent Technologies to Realize the Metaverse
Oct 03, 2022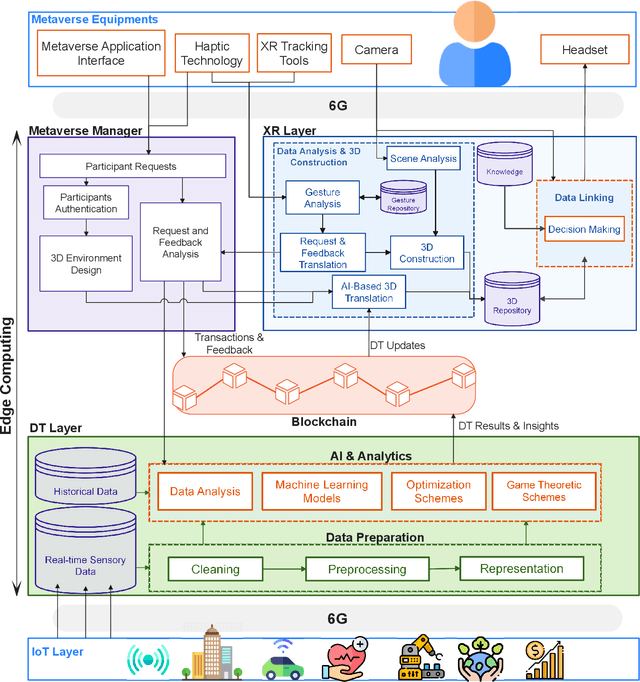
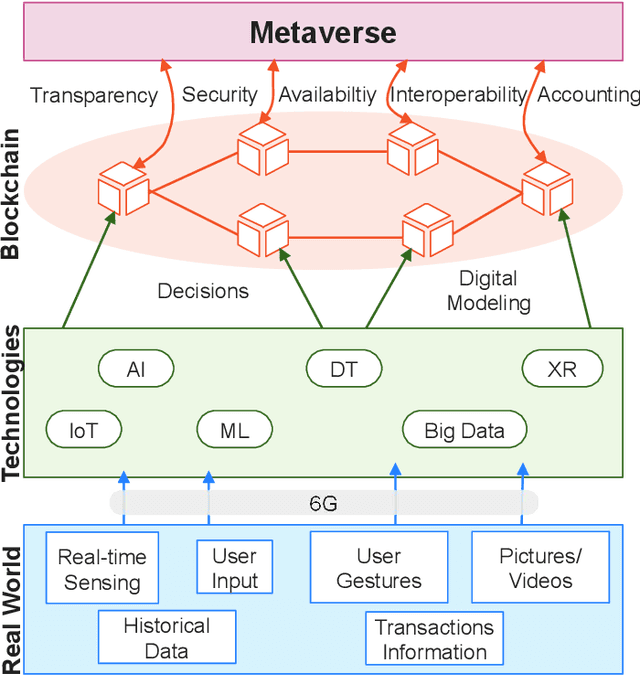
Abstract:The advances in Artificial Intelligence (AI) have led to technological advancements in a plethora of domains. Healthcare, education, and smart city services are now enriched with AI capabilities. These technological advancements would not have been realized without the assistance of fast, secure, and fault-tolerant communication media. Traditional processing, communication and storage technologies cannot maintain high levels of scalability and user experience for immersive services. The metaverse is an immersive three-dimensional (3D) virtual world that integrates fantasy and reality into a virtual environment using advanced virtual reality (VR) and augmented reality (AR) devices. Such an environment is still being developed and requires extensive research in order for it to be realized to its highest attainable levels. In this article, we discuss some of the key issues required in order to attain realization of metaverse services. We propose a framework that integrates digital twin (DT) with other advanced technologies such as the sixth generation (6G) communication network, blockchain, and AI, to maintain continuous end-to-end metaverse services. This article also outlines requirements for an integrated, DT-enabled metaverse framework and provides a look ahead into the evolving topic.
Internet of Things Device Capabilities, Architectures, Protocols, and Smart Applications in Healthcare Domain: A Review
Apr 12, 2022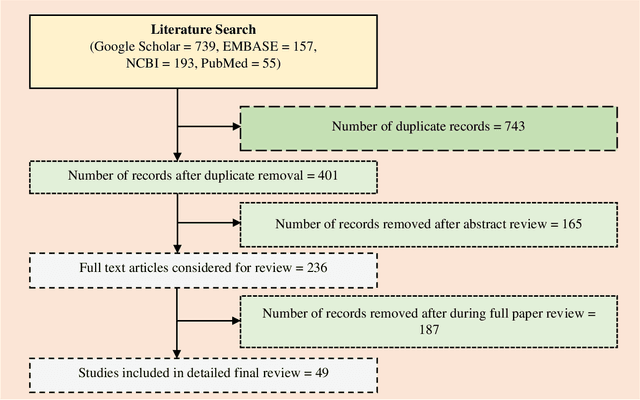
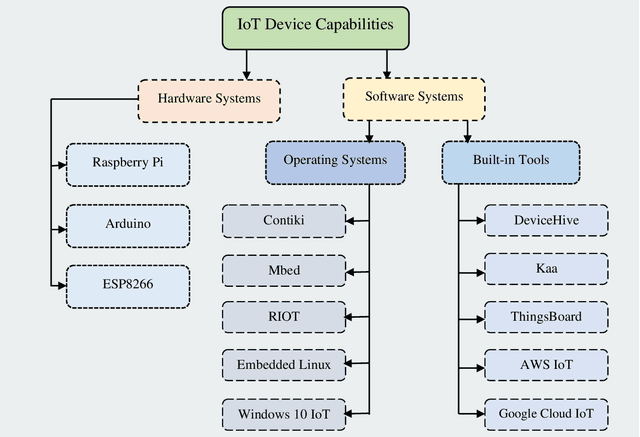
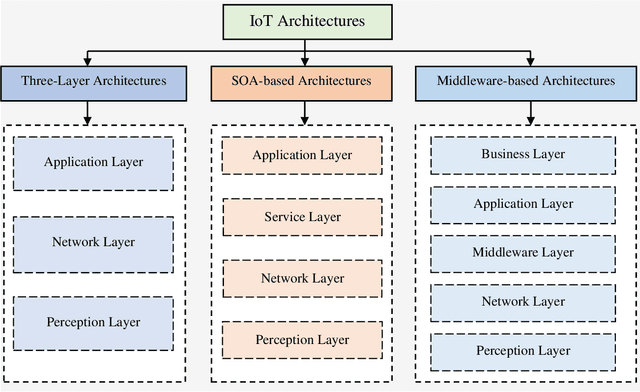
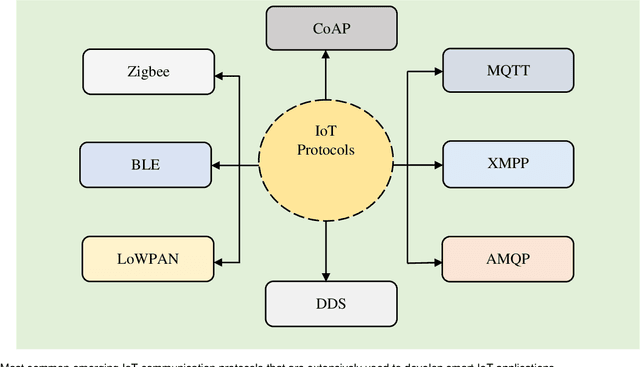
Abstract:Nowadays, the Internet has spread to practically every country around the world and is having unprecedented effects on people's lives. The Internet of Things (IoT) is getting more popular and has a high level of interest in both practitioners and academicians in the age of wireless communication due to its diverse applications. The IoT is a technology that enables everyday things to become savvier, everyday computation towards becoming intellectual, and everyday communication to become a little more insightful. In this paper, the most common and popular IoT device capabilities, architectures, and protocols are demonstrated in brief to provide a clear overview of the IoT technology to the researchers in this area. The common IoT device capabilities including hardware (Raspberry Pi, Arduino, and ESP8266) and software (operating systems, and built-in tools) platforms are described in detail. The widely used architectures that have been recently evolved and used are the three-layer architecture, SOA-based architecture, and middleware-based architecture. The popular protocols for IoT are demonstrated which include CoAP, MQTT, XMPP, AMQP, DDS, LoWPAN, BLE, and Zigbee that are frequently utilized to develop smart IoT applications. Additionally, this research provides an in-depth overview of the potential healthcare applications based on IoT technologies in the context of addressing various healthcare concerns. Finally, this paper summarizes state-of-the-art knowledge, highlights open issues and shortcomings, and provides recommendations for further studies which would be quite beneficial to anyone with a desire to work in this field and make breakthroughs to get expertise in this area.
Theoretical Connection between Locally Linear Embedding, Factor Analysis, and Probabilistic PCA
Mar 25, 2022Abstract:Locally Linear Embedding (LLE) is a nonlinear spectral dimensionality reduction and manifold learning method. It has two main steps which are linear reconstruction and linear embedding of points in the input space and embedding space, respectively. In this work, we look at the linear reconstruction step from a stochastic perspective where it is assumed that every data point is conditioned on its linear reconstruction weights as latent factors. The stochastic linear reconstruction of LLE is solved using expectation maximization. We show that there is a theoretical connection between three fundamental dimensionality reduction methods, i.e., LLE, factor analysis, and probabilistic Principal Component Analysis (PCA). The stochastic linear reconstruction of LLE is formulated similar to the factor analysis and probabilistic PCA. It is also explained why factor analysis and probabilistic PCA are linear and LLE is a nonlinear method. This work combines and makes a bridge between two broad approaches of dimensionality reduction, i.e., the spectral and probabilistic algorithms.
On Manifold Hypothesis: Hypersurface Submanifold Embedding Using Osculating Hyperspheres
Feb 03, 2022Abstract:Consider a set of $n$ data points in the Euclidean space $\mathbb{R}^d$. This set is called dataset in machine learning and data science. Manifold hypothesis states that the dataset lies on a low-dimensional submanifold with high probability. All dimensionality reduction and manifold learning methods have the assumption of manifold hypothesis. In this paper, we show that the dataset lies on an embedded hypersurface submanifold which is locally $(d-1)$-dimensional. Hence, we show that the manifold hypothesis holds at least for the embedding dimensionality $d-1$. Using an induction in a pyramid structure, we also extend the embedding dimensionality to lower embedding dimensionalities to show the validity of manifold hypothesis for embedding dimensionalities $\{1, 2, \dots, d-1\}$. For embedding the hypersurface, we first construct the $d$ nearest neighbors graph for data. For every point, we fit an osculating hypersphere $S^{d-1}$ using its neighbors where this hypersphere is osculating to a hypothetical hypersurface. Then, using surgery theory, we apply surgery on the osculating hyperspheres to obtain $n$ hyper-caps. We connect the hyper-caps to one another using partial hyper-cylinders. By connecting all parts, the embedded hypersurface is obtained as the disjoint union of these elements. We discuss the geometrical characteristics of the embedded hypersurface, such as having boundary, its topology, smoothness, boundedness, orientability, compactness, and injectivity. Some discussion are also provided for the linearity and structure of data. This paper is the intersection of several fields of science including machine learning, differential geometry, and algebraic topology.
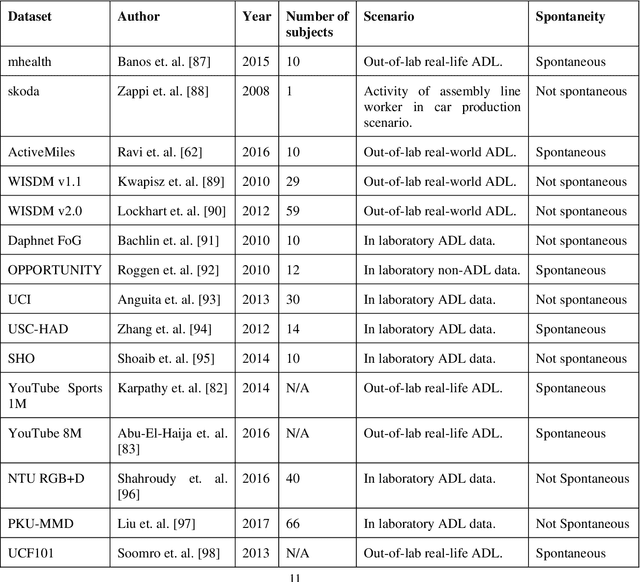
Human Activity Recognition Using Tools of Convolutional Neural Networks: A State of the Art Review, Data Sets, Challenges and Future Prospects
Feb 02, 2022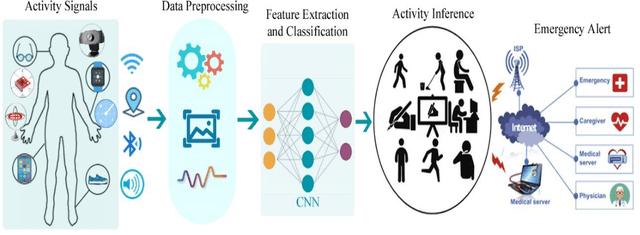
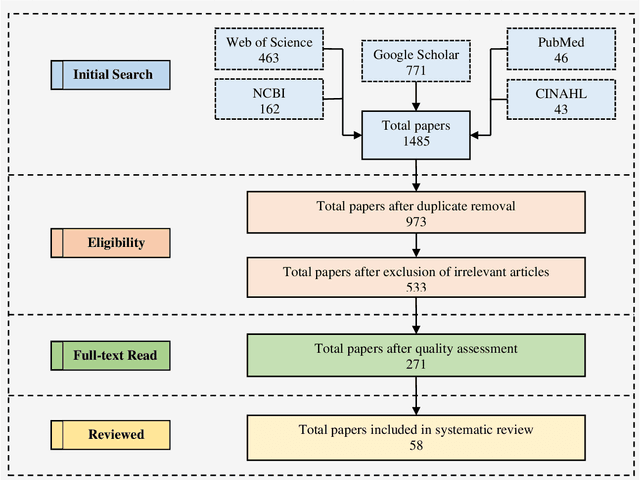
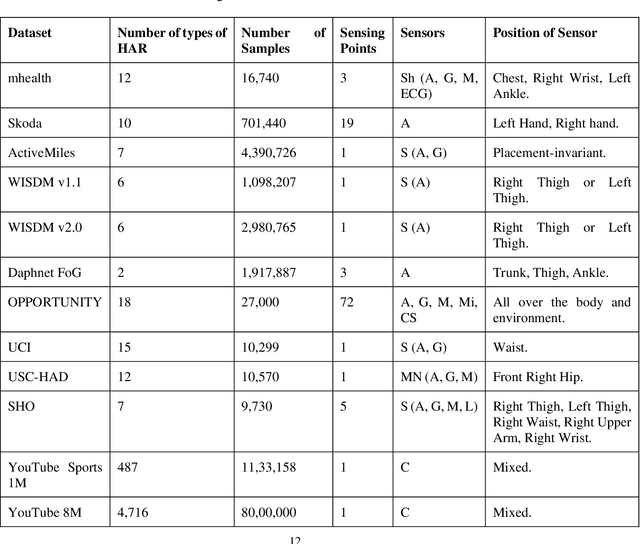
Abstract:Human Activity Recognition (HAR) plays a significant role in the everyday life of people because of its ability to learn extensive high-level information about human activity from wearable or stationary devices. A substantial amount of research has been conducted on HAR and numerous approaches based on deep learning and machine learning have been exploited by the research community to classify human activities. The main goal of this review is to summarize recent works based on a wide range of deep neural networks architecture, namely convolutional neural networks (CNNs) for human activity recognition. The reviewed systems are clustered into four categories depending on the use of input devices like multimodal sensing devices, smartphones, radar, and vision devices. This review describes the performances, strengths, weaknesses, and the used hyperparameters of CNN architectures for each reviewed system with an overview of available public data sources. In addition, a discussion with the current challenges to CNN-based HAR systems is presented. Finally, this review is concluded with some potential future directions that would be of great assistance for the researchers who would like to contribute to this field.
Spectral, Probabilistic, and Deep Metric Learning: Tutorial and Survey
Jan 23, 2022Abstract:This is a tutorial and survey paper on metric learning. Algorithms are divided into spectral, probabilistic, and deep metric learning. We first start with the definition of distance metric, Mahalanobis distance, and generalized Mahalanobis distance. In spectral methods, we start with methods using scatters of data, including the first spectral metric learning, relevant methods to Fisher discriminant analysis, Relevant Component Analysis (RCA), Discriminant Component Analysis (DCA), and the Fisher-HSIC method. Then, large-margin metric learning, imbalanced metric learning, locally linear metric adaptation, and adversarial metric learning are covered. We also explain several kernel spectral methods for metric learning in the feature space. We also introduce geometric metric learning methods on the Riemannian manifolds. In probabilistic methods, we start with collapsing classes in both input and feature spaces and then explain the neighborhood component analysis methods, Bayesian metric learning, information theoretic methods, and empirical risk minimization in metric learning. In deep learning methods, we first introduce reconstruction autoencoders and supervised loss functions for metric learning. Then, Siamese networks and its various loss functions, triplet mining, and triplet sampling are explained. Deep discriminant analysis methods, based on Fisher discriminant analysis, are also reviewed. Finally, we introduce multi-modal deep metric learning, geometric metric learning by neural networks, and few-shot metric learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge