Sharper Convergence Rates for Nonconvex Optimisation via Reduction Mappings

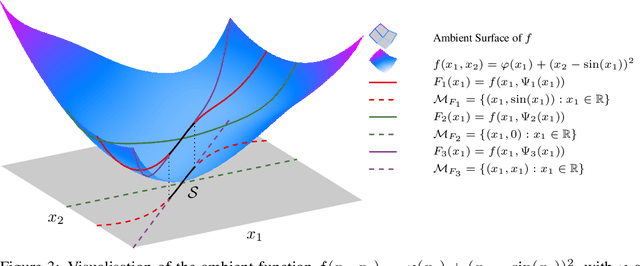
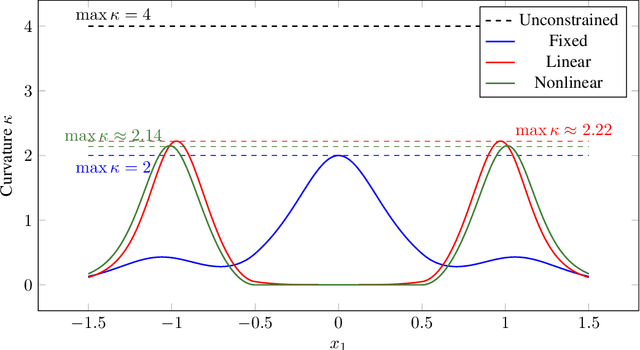
Many high-dimensional optimisation problems exhibit rich geometric structures in their set of minimisers, often forming smooth manifolds due to over-parametrisation or symmetries. When this structure is known, at least locally, it can be exploited through reduction mappings that reparametrise part of the parameter space to lie on the solution manifold. These reductions naturally arise from inner optimisation problems and effectively remove redundant directions, yielding a lower-dimensional objective. In this work, we introduce a general framework to understand how such reductions influence the optimisation landscape. We show that well-designed reduction mappings improve curvature properties of the objective, leading to better-conditioned problems and theoretically faster convergence for gradient-based methods. Our analysis unifies a range of scenarios where structural information at optimality is leveraged to accelerate convergence, offering a principled explanation for the empirical gains observed in such optimisation algorithms.

Guiding Neural Collapse: Optimising Towards the Nearest Simplex Equiangular Tight Frame

Neural Collapse (NC) is a recently observed phenomenon in neural networks that characterises the solution space of the final classifier layer when trained until zero training loss. Specifically, NC suggests that the final classifier layer converges to a Simplex Equiangular Tight Frame (ETF), which maximally separates the weights corresponding to each class. By duality, the penultimate layer feature means also converge to the same simplex ETF. Since this simple symmetric structure is optimal, our idea is to utilise this property to improve convergence speed. Specifically, we introduce the notion of nearest simplex ETF geometry for the penultimate layer features at any given training iteration, by formulating it as a Riemannian optimisation. Then, at each iteration, the classifier weights are implicitly set to the nearest simplex ETF by solving this inner-optimisation, which is encapsulated within a declarative node to allow backpropagation. Our experiments on synthetic and real-world architectures for classification tasks demonstrate that our approach accelerates convergence and enhances training stability.