ELIS: Efficient LLM Iterative Scheduling System with Response Length Predictor

We propose ELIS, a serving system for Large Language Models (LLMs) featuring an Iterative Shortest Remaining Time First (ISRTF) scheduler designed to efficiently manage inference tasks with the shortest remaining tokens. Current LLM serving systems often employ a first-come-first-served scheduling strategy, which can lead to the "head-of-line blocking" problem. To overcome this limitation, it is necessary to predict LLM inference times and apply a shortest job first scheduling strategy. However, due to the auto-regressive nature of LLMs, predicting the inference latency is challenging. ELIS addresses this challenge by training a response length predictor for LLMs using the BGE model, an encoder-based state-of-the-art model. Additionally, we have devised the ISRTF scheduling strategy, an optimization of shortest remaining time first tailored to existing LLM iteration batching. To evaluate our work in an industrial setting, we simulate streams of requests based on our study of real-world user LLM serving trace records. Furthermore, we implemented ELIS as a cloud-native scheduler system on Kubernetes to evaluate its performance in production environments. Our experimental results demonstrate that ISRTF reduces the average job completion time by up to 19.6%.

Line Graph Vietoris-Rips Persistence Diagram for Topological Graph Representation Learning

While message passing graph neural networks result in informative node embeddings, they may suffer from describing the topological properties of graphs. To this end, node filtration has been widely used as an attempt to obtain the topological information of a graph using persistence diagrams. However, these attempts have faced the problem of losing node embedding information, which in turn prevents them from providing a more expressive graph representation. To tackle this issue, we shift our focus to edge filtration and introduce a novel edge filtration-based persistence diagram, named Topological Edge Diagram (TED), which is mathematically proven to preserve node embedding information as well as contain additional topological information. To implement TED, we propose a neural network based algorithm, named Line Graph Vietoris-Rips (LGVR) Persistence Diagram, that extracts edge information by transforming a graph into its line graph. Through LGVR, we propose two model frameworks that can be applied to any message passing GNNs, and prove that they are strictly more powerful than Weisfeiler-Lehman type colorings. Finally we empirically validate superior performance of our models on several graph classification and regression benchmarks.

SEEN: Sharpening Explanations for Graph Neural Networks using Explanations from Neighborhoods

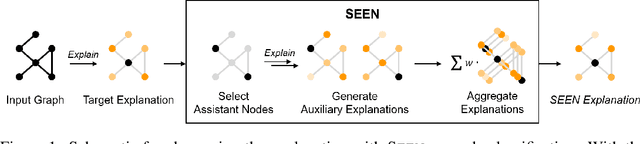
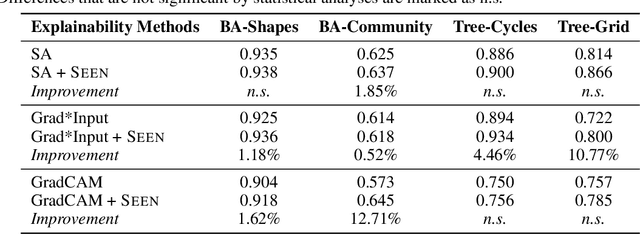
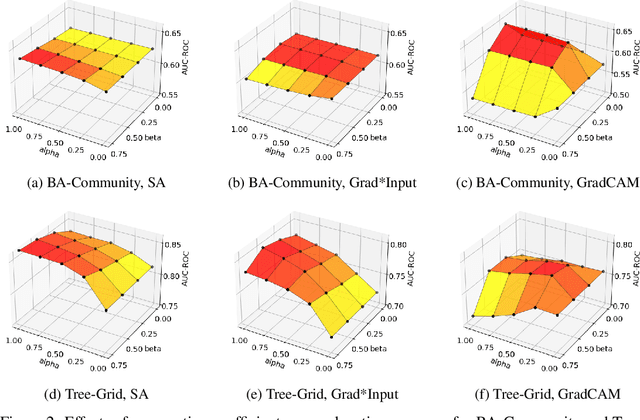
Explaining the foundations for predictions obtained from graph neural networks (GNNs) is critical for credible use of GNN models for real-world problems. Owing to the rapid growth of GNN applications, recent progress in explaining predictions from GNNs, such as sensitivity analysis, perturbation methods, and attribution methods, showed great opportunities and possibilities for explaining GNN predictions. In this study, we propose a method to improve the explanation quality of node classification tasks that can be applied in a post hoc manner through aggregation of auxiliary explanations from important neighboring nodes, named SEEN. Applying SEEN does not require modification of a graph and can be used with diverse explainability techniques due to its independent mechanism. Experiments on matching motif-participating nodes from a given graph show great improvement in explanation accuracy of up to 12.71% and demonstrate the correlation between the auxiliary explanations and the enhanced explanation accuracy through leveraging their contributions. SEEN provides a simple but effective method to enhance the explanation quality of GNN model outputs, and this method is applicable in combination with most explainability techniques.