Compatibility of Multiple Control Barrier Functions for Constrained Nonlinear Systems

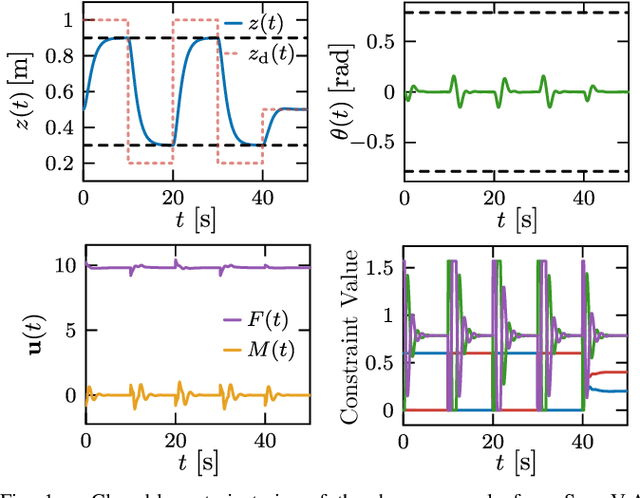
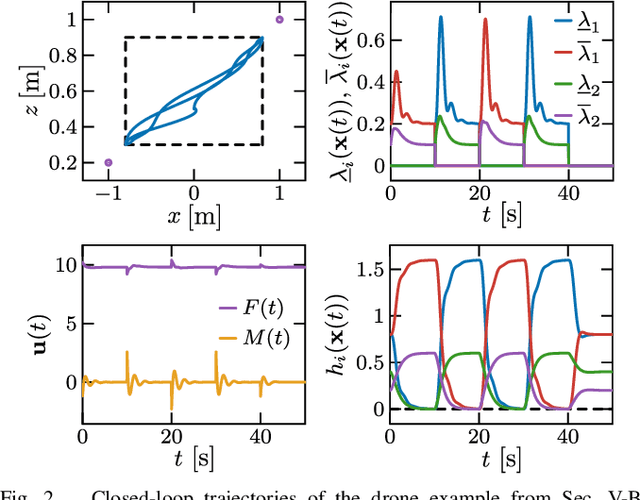
Control barrier functions (CBFs) are a powerful tool for the constrained control of nonlinear systems; however, the majority of results in the literature focus on systems subject to a single CBF constraint, making it challenging to synthesize provably safe controllers that handle multiple state constraints. This paper presents a framework for constrained control of nonlinear systems subject to box constraints on the systems' vector-valued outputs using multiple CBFs. Our results illustrate that when the output has a vector relative degree, the CBF constraints encoding these box constraints are compatible, and the resulting optimization-based controller is locally Lipschitz continuous and admits a closed-form expression. Additional results are presented to characterize the degradation of nominal tracking objectives in the presence of safety constraints. Simulations of a planar quadrotor are presented to demonstrate the efficacy of the proposed framework.

Parameter Estimation in Adaptive Control of Time-Varying Systems Under a Range of Excitation Conditions

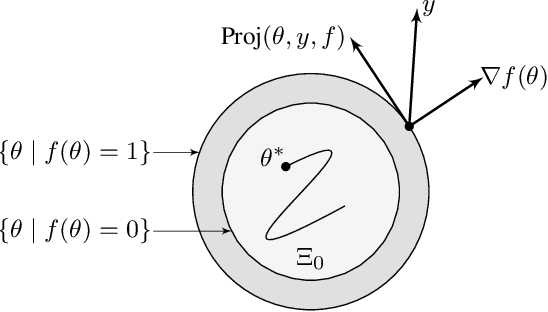
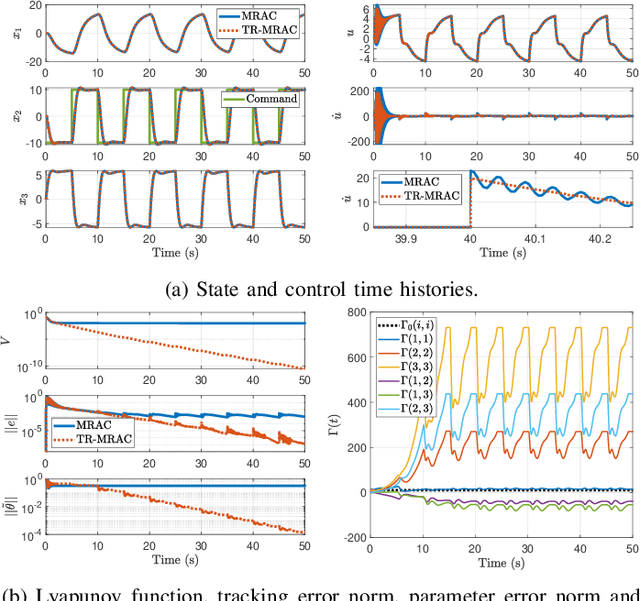
This paper presents a new parameter estimation algorithm for the adaptive control of a class of time-varying plants. The main feature of this algorithm is a matrix of time-varying learning rates, which enables parameter estimation error trajectories to tend exponentially fast towards a compact set whenever excitation conditions are satisfied. This algorithm is employed in a large class of problems where unknown parameters are present and are time-varying. It is shown that this algorithm guarantees global boundedness of the state and parameter errors of the system, and avoids an often used filtering approach for constructing key regressor signals. In addition, intervals of time over which these errors tend exponentially fast toward a compact set are provided, both in the presence of finite and persistent excitation. A projection operator is used to ensure the boundedness of the learning rate matrix, as compared to a time-varying forgetting factor. Numerical simulations are provided to complement the theoretical analysis.

Connections Between Adaptive Control and Optimization in Machine Learning

This paper demonstrates many immediate connections between adaptive control and optimization methods commonly employed in machine learning. Starting from common output error formulations, similarities in update law modifications are examined. Concepts in stability, performance, and learning, common to both fields are then discussed. Building on the similarities in update laws and common concepts, new intersections and opportunities for improved algorithm analysis are provided. In particular, a specific problem related to higher order learning is solved through insights obtained from these intersections.