Geometric Feature Prompting of Image Segmentation Models

Advances in machine learning, especially the introduction of transformer architectures and vision transformers, have led to the development of highly capable computer vision foundation models. The segment anything model (known colloquially as SAM and more recently SAM 2), is a highly capable foundation model for segmentation of natural images and has been further applied to medical and scientific image segmentation tasks. SAM relies on prompts -- points or regions of interest in an image -- to generate associated segmentations. In this manuscript we propose the use of a geometrically motivated prompt generator to produce prompt points that are colocated with particular features of interest. Focused prompting enables the automatic generation of sensitive and specific segmentations in a scientific image analysis task using SAM with relatively few point prompts. The image analysis task examined is the segmentation of plant roots in rhizotron or minirhizotron images, which has historically been a difficult task to automate. Hand annotation of rhizotron images is laborious and often subjective; SAM, initialized with GeomPrompt local ridge prompts has the potential to dramatically improve rhizotron image processing. The authors have concurrently released an open source software suite called geomprompt https://pypi.org/project/geomprompt/ that can produce point prompts in a format that enables direct integration with the segment-anything package.

Multi-Robot Motion Planning for Unit Discs with Revolving Areas

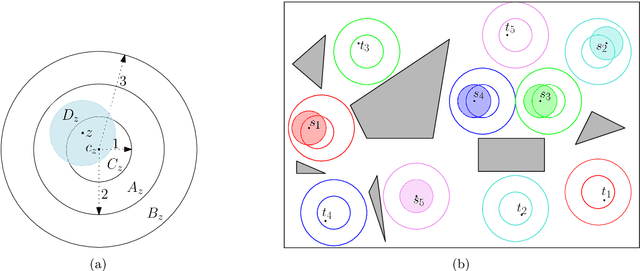
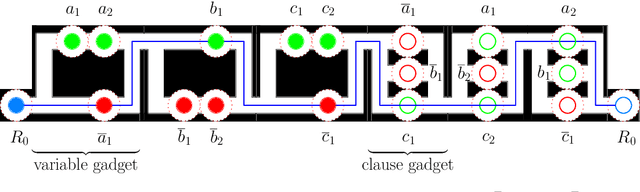
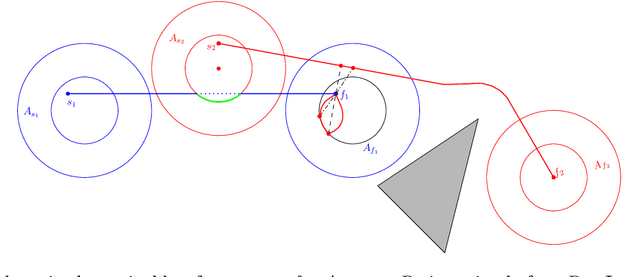
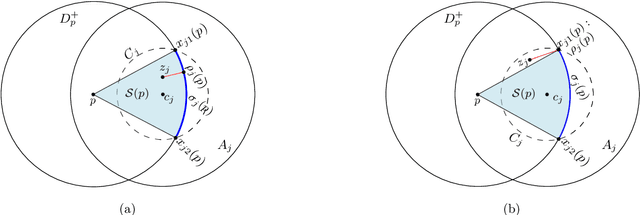
We study the problem of motion planning for a collection of $n$ labeled unit disc robots in a polygonal environment. We assume that the robots have \emph{revolving areas} around their start and final positions: that each start and each final is contained in a radius $2$ disc lying in the free space, not necessarily concentric with the start or final position, which is free from other start or final positions. This assumption allows a \emph{weakly-monotone} motion plan, in which robots move according to an ordering as follows: during the turn of a robot $R$ in the ordering, it moves fully from its start to final position, while other robots do not leave their revolving areas. As $R$ passes through a revolving area, a robot $R'$ that is inside this area may move within the revolving area to avoid a collision. Notwithstanding the existence of a motion plan, we show that minimizing the total traveled distance in this setting, specifically even when the motion plan is restricted to be weakly-monotone, is APX-hard, ruling out any polynomial-time $(1+\epsilon)$-approximation algorithm. On the positive side, we present the first constant-factor approximation algorithm for computing a feasible weakly-monotone motion plan. The total distance traveled by the robots is within an $O(1)$ factor of that of the optimal motion plan, which need not be weakly monotone. Our algorithm extends to an online setting in which the polygonal environment is fixed but the initial and final positions of robots are specified in an online manner. Finally, we observe that the overhead in the overall cost that we add while editing the paths to avoid robot-robot collision can vary significantly depending on the ordering we chose. Finding the best ordering in this respect is known to be NP-hard, and we provide a polynomial time $O(\log n \log \log n)$-approximation algorithm for this problem.