Eric Lippert
PPL Bench: Evaluation Framework For Probabilistic Programming Languages
Oct 17, 2020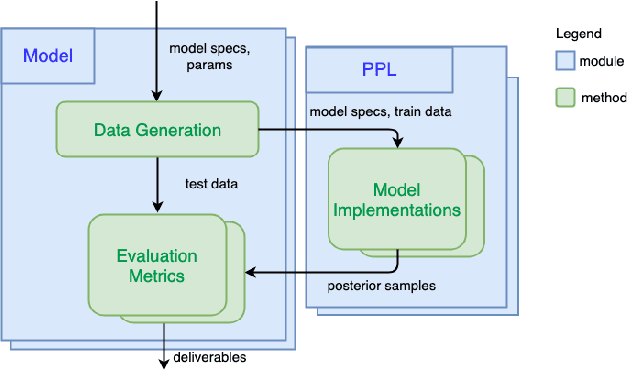
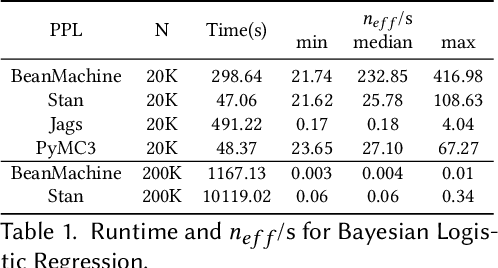
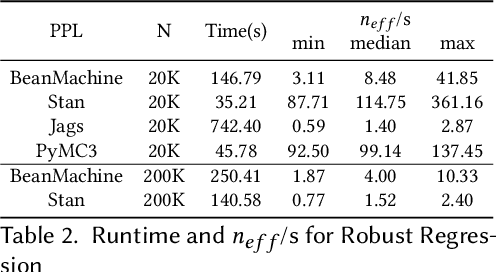
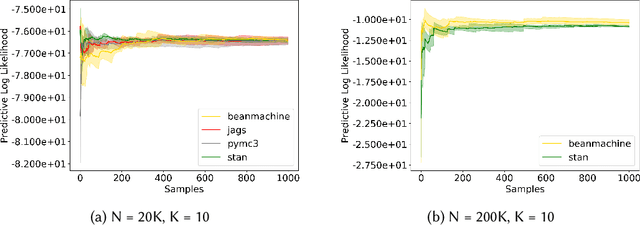
Abstract:We introduce PPL Bench, a new benchmark for evaluating Probabilistic Programming Languages (PPLs) on a variety of statistical models. The benchmark includes data generation and evaluation code for a number of models as well as implementations in some common PPLs. All of the benchmark code and PPL implementations are available on Github. We welcome contributions of new models and PPLs and as well as improvements in existing PPL implementations. The purpose of the benchmark is two-fold. First, we want researchers as well as conference reviewers to be able to evaluate improvements in PPLs in a standardized setting. Second, we want end users to be able to pick the PPL that is most suited for their modeling application. In particular, we are interested in evaluating the accuracy and speed of convergence of the inferred posterior. Each PPL only needs to provide posterior samples given a model and observation data. The framework automatically computes and plots growth in predictive log-likelihood on held out data in addition to reporting other common metrics such as effective sample size and $\hat{r}$.
Newtonian Monte Carlo: single-site MCMC meets second-order gradient methods
Jan 15, 2020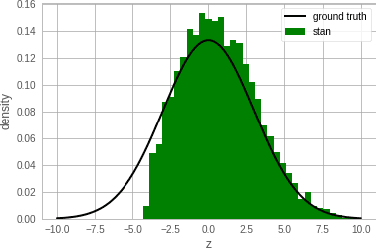

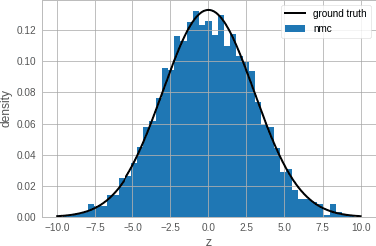
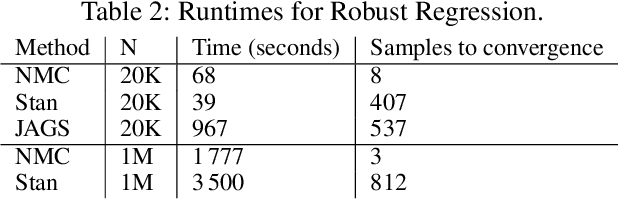
Abstract:Single-site Markov Chain Monte Carlo (MCMC) is a variant of MCMC in which a single coordinate in the state space is modified in each step. Structured relational models are a good candidate for this style of inference. In the single-site context, second order methods become feasible because the typical cubic costs associated with these methods is now restricted to the dimension of each coordinate. Our work, which we call Newtonian Monte Carlo (NMC), is a method to improve MCMC convergence by analyzing the first and second order gradients of the target density to determine a suitable proposal density at each point. Existing first order gradient-based methods suffer from the problem of determining an appropriate step size. Too small a step size and it will take a large number of steps to converge, while a very large step size will cause it to overshoot the high density region. NMC is similar to the Newton-Raphson update in optimization where the second order gradient is used to automatically scale the step size in each dimension. However, our objective is to find a parameterized proposal density rather than the maxima. As a further improvement on existing first and second order methods, we show that random variables with constrained supports don't need to be transformed before taking a gradient step. We demonstrate the efficiency of NMC on a number of different domains. For statistical models where the prior is conjugate to the likelihood, our method recovers the posterior quite trivially in one step. However, we also show results on fairly large non-conjugate models, where NMC performs better than adaptive first order methods such as NUTS or other inexact scalable inference methods such as Stochastic Variational Inference or bootstrapping.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge