Splitting Methods for Convex Clustering

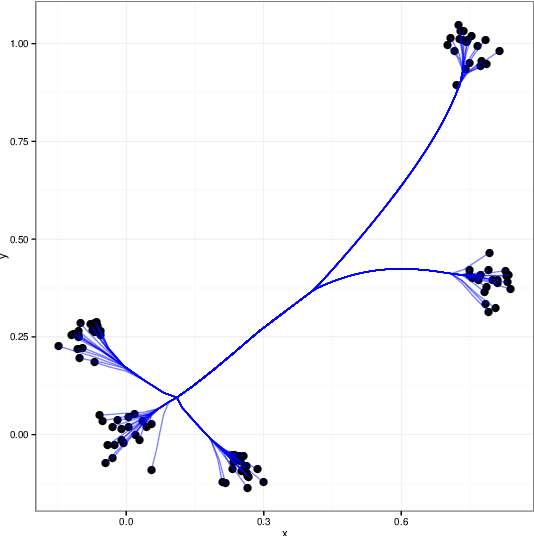
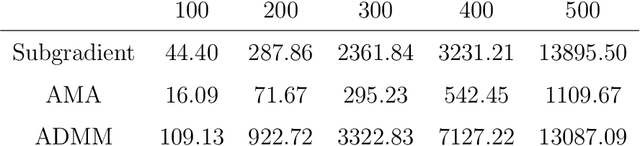
Clustering is a fundamental problem in many scientific applications. Standard methods such as $k$-means, Gaussian mixture models, and hierarchical clustering, however, are beset by local minima, which are sometimes drastically suboptimal. Recently introduced convex relaxations of $k$-means and hierarchical clustering shrink cluster centroids toward one another and ensure a unique global minimizer. In this work we present two splitting methods for solving the convex clustering problem. The first is an instance of the alternating direction method of multipliers (ADMM); the second is an instance of the alternating minimization algorithm (AMA). In contrast to previously considered algorithms, our ADMM and AMA formulations provide simple and unified frameworks for solving the convex clustering problem under the previously studied norms and open the door to potentially novel norms. We demonstrate the performance of our algorithm on both simulated and real data examples. While the differences between the two algorithms appear to be minor on the surface, complexity analysis and numerical experiments show AMA to be significantly more efficient.

Distance Majorization and Its Applications

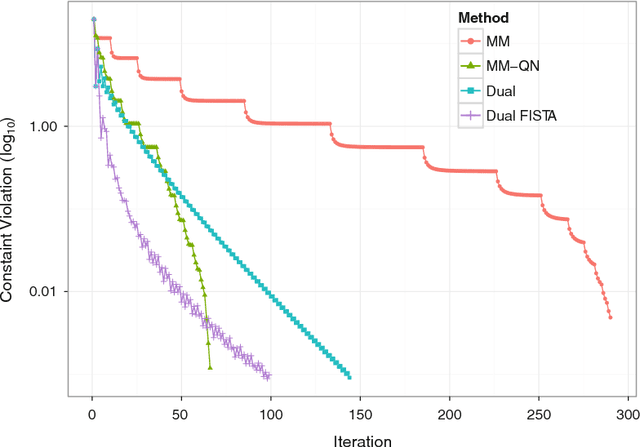
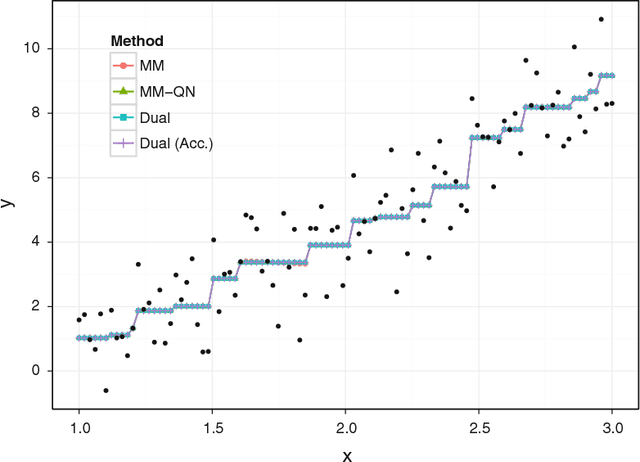
The problem of minimizing a continuously differentiable convex function over an intersection of closed convex sets is ubiquitous in applied mathematics. It is particularly interesting when it is easy to project onto each separate set, but nontrivial to project onto their intersection. Algorithms based on Newton's method such as the interior point method are viable for small to medium-scale problems. However, modern applications in statistics, engineering, and machine learning are posing problems with potentially tens of thousands of parameters or more. We revisit this convex programming problem and propose an algorithm that scales well with dimensionality. Our proposal is an instance of a sequential unconstrained minimization technique and revolves around three ideas: the majorization-minimization (MM) principle, the classical penalty method for constrained optimization, and quasi-Newton acceleration of fixed-point algorithms. The performance of our distance majorization algorithms is illustrated in several applications.

Robust Parametric Classification and Variable Selection by a Minimum Distance Criterion

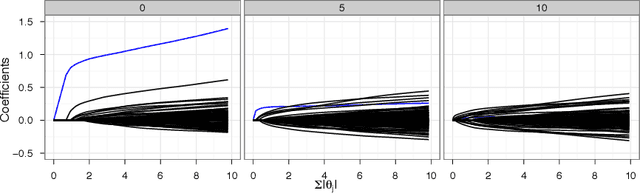
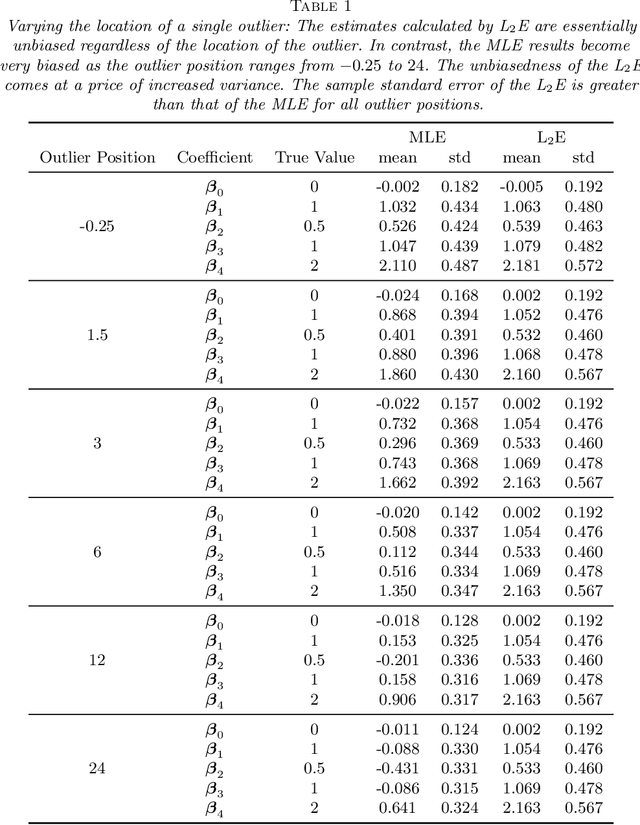
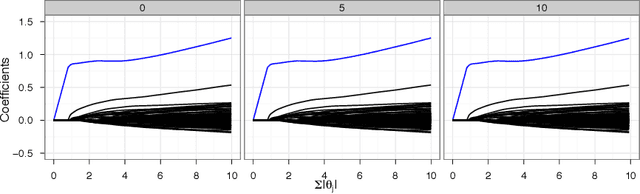
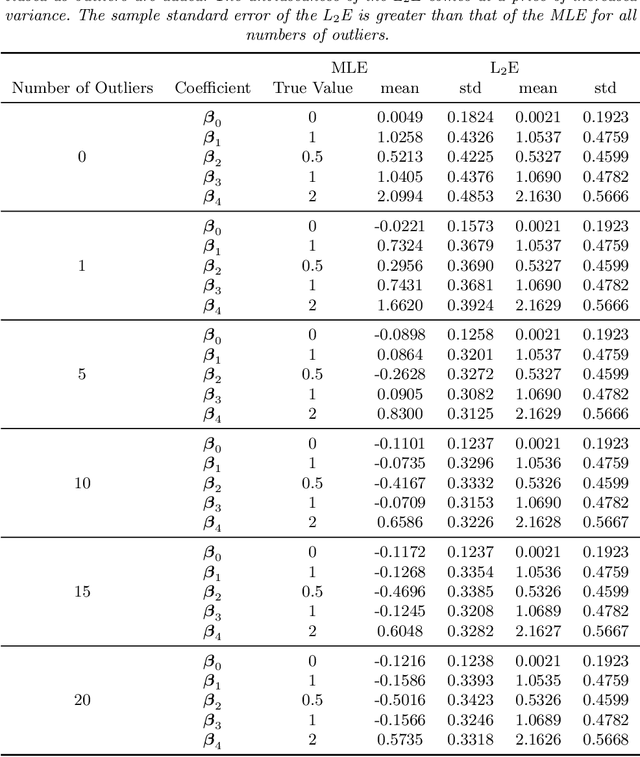
We investigate a robust penalized logistic regression algorithm based on a minimum distance criterion. Influential outliers are often associated with the explosion of parameter vector estimates, but in the context of standard logistic regression, the bias due to outliers always causes the parameter vector to implode, that is shrink towards the zero vector. Thus, using LASSO-like penalties to perform variable selection in the presence of outliers can result in missed detections of relevant covariates. We show that by choosing a minimum distance criterion together with an Elastic Net penalty, we can simultaneously find a parsimonious model and avoid estimation implosion even in the presence of many outliers in the important small $n$ large $p$ situation. Implementation using an MM algorithm is described and performance evaluated.