Nonparametric Density Estimation for High-Dimensional Data - Algorithms and Applications

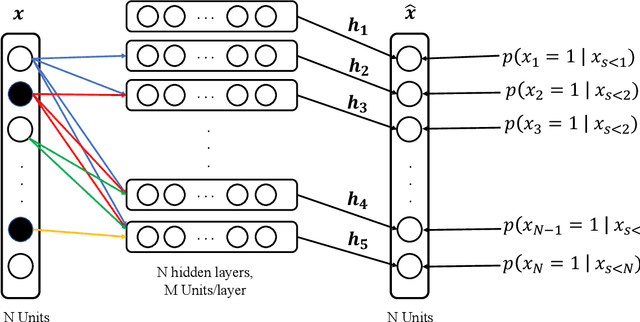
Density Estimation is one of the central areas of statistics whose purpose is to estimate the probability density function underlying the observed data. It serves as a building block for many tasks in statistical inference, visualization, and machine learning. Density Estimation is widely adopted in the domain of unsupervised learning especially for the application of clustering. As big data become pervasive in almost every area of data sciences, analyzing high-dimensional data that have many features and variables appears to be a major focus in both academia and industry. High-dimensional data pose challenges not only from the theoretical aspects of statistical inference, but also from the algorithmic/computational considerations of machine learning and data analytics. This paper reviews a collection of selected nonparametric density estimation algorithms for high-dimensional data, some of them are recently published and provide interesting mathematical insights. The important application domain of nonparametric density estimation, such as { modal clustering}, are also included in this paper. Several research directions related to density estimation and high-dimensional data analysis are suggested by the authors.

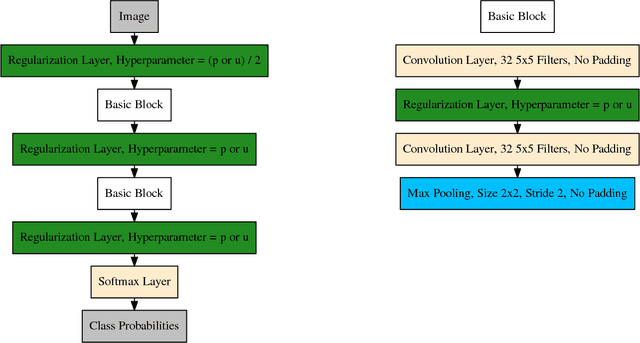
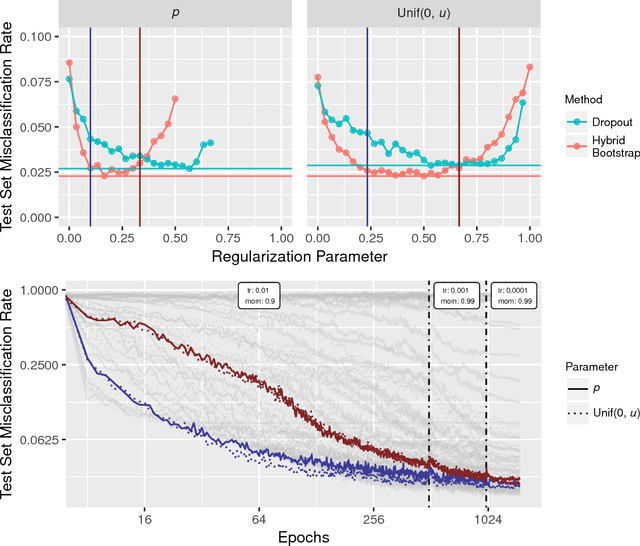
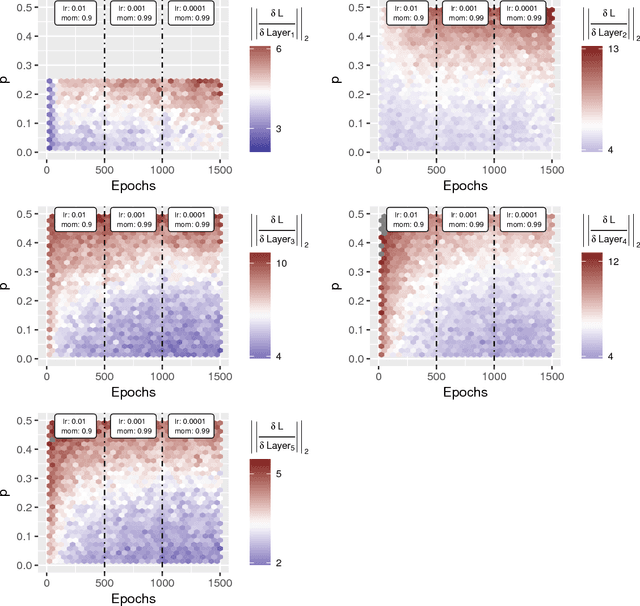
The Hybrid Bootstrap: A Drop-in Replacement for Dropout

Regularization is an important component of predictive model building. The hybrid bootstrap is a regularization technique that functions similarly to dropout except that features are resampled from other training points rather than replaced with zeros. We show that the hybrid bootstrap offers superior performance to dropout. We also present a sampling based technique to simplify hyperparameter choice. Next, we provide an alternative sampling technique for convolutional neural networks. Finally, we demonstrate the efficacy of the hybrid bootstrap on non-image tasks using tree-based models.

Robust Parametric Classification and Variable Selection by a Minimum Distance Criterion

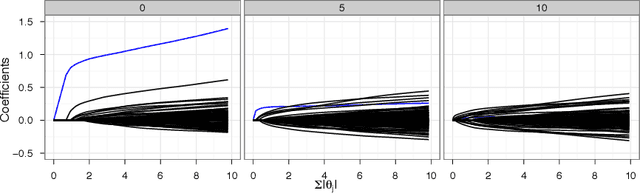
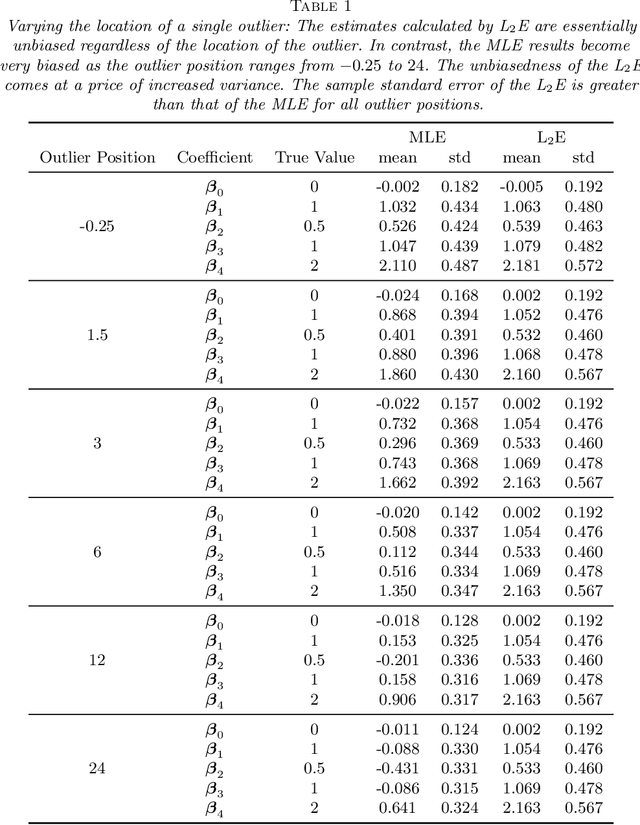
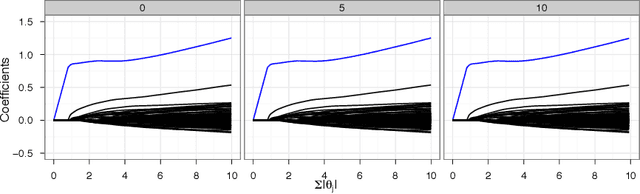
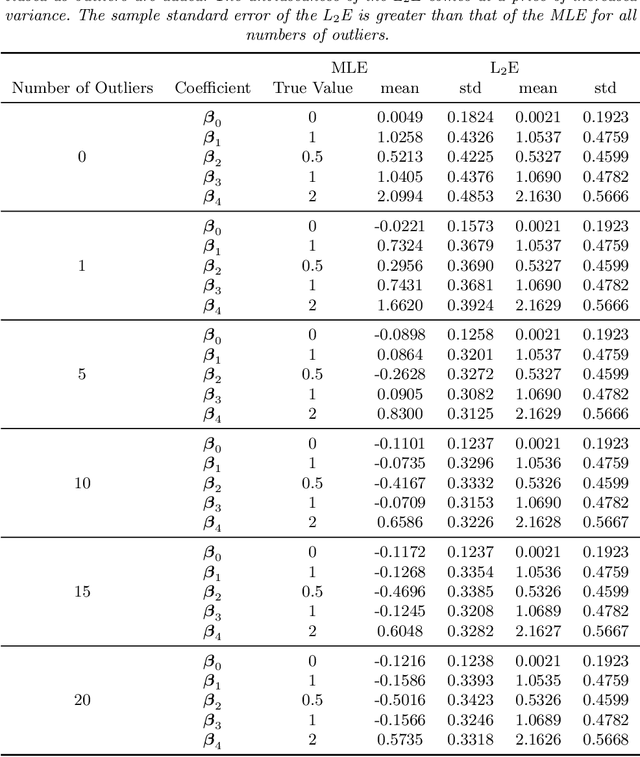
We investigate a robust penalized logistic regression algorithm based on a minimum distance criterion. Influential outliers are often associated with the explosion of parameter vector estimates, but in the context of standard logistic regression, the bias due to outliers always causes the parameter vector to implode, that is shrink towards the zero vector. Thus, using LASSO-like penalties to perform variable selection in the presence of outliers can result in missed detections of relevant covariates. We show that by choosing a minimum distance criterion together with an Elastic Net penalty, we can simultaneously find a parsimonious model and avoid estimation implosion even in the presence of many outliers in the important small $n$ large $p$ situation. Implementation using an MM algorithm is described and performance evaluated.