Geographical Context Matters: Bridging Fine and Coarse Spatial Information to Enhance Continental Land Cover Mapping

Land use and land cover mapping from Earth Observation (EO) data is a critical tool for sustainable land and resource management. While advanced machine learning and deep learning algorithms excel at analyzing EO imagery data, they often overlook crucial geospatial metadata information that could enhance scalability and accuracy across regional, continental, and global scales. To address this limitation, we propose BRIDGE-LC (Bi-level Representation Integration for Disentangled GEospatial Land Cover), a novel deep learning framework that integrates multi-scale geospatial information into the land cover classification process. By simultaneously leveraging fine-grained (latitude/longitude) and coarse-grained (biogeographical region) spatial information, our lightweight multi-layer perceptron architecture learns from both during training but only requires fine-grained information for inference, allowing it to disentangle region-specific from region-agnostic land cover features while maintaining computational efficiency. To assess the quality of our framework, we use an open-access in-situ dataset and adopt several competing classification approaches commonly considered for large-scale land cover mapping. We evaluated all approaches through two scenarios: an extrapolation scenario in which training data encompasses samples from all biogeographical regions, and a leave-one-region-out scenario where one region is excluded from training. We also explore the spatial representation learned by our model, highlighting a connection between its internal manifold and the geographical information used during training. Our results demonstrate that integrating geospatial information improves land cover mapping performance, with the most substantial gains achieved by jointly leveraging both fine- and coarse-grained spatial information.

Optimized Kernel Entropy Components

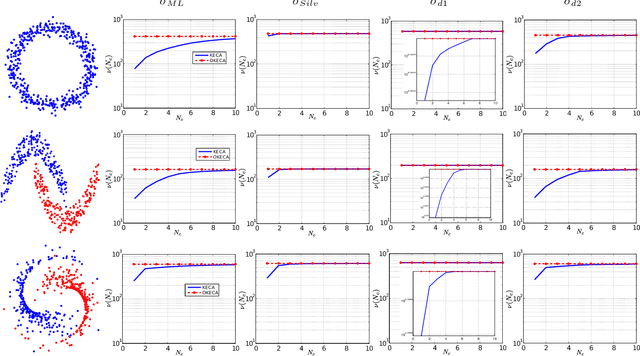
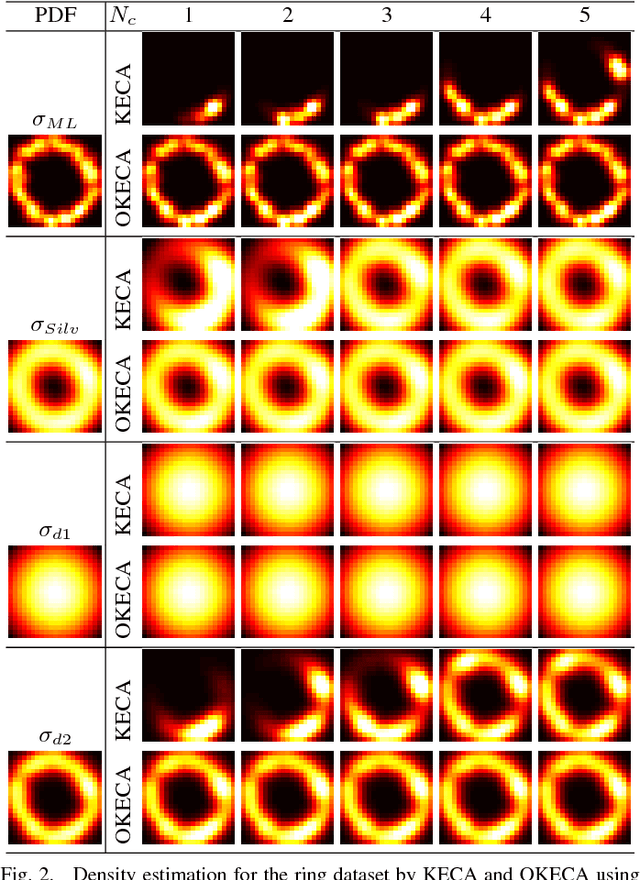
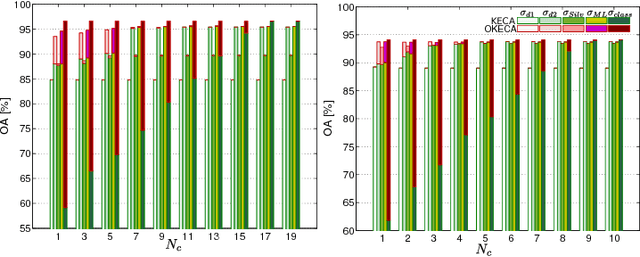
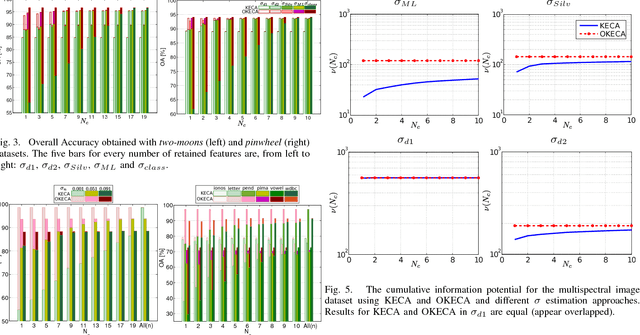
This work addresses two main issues of the standard Kernel Entropy Component Analysis (KECA) algorithm: the optimization of the kernel decomposition and the optimization of the Gaussian kernel parameter. KECA roughly reduces to a sorting of the importance of kernel eigenvectors by entropy instead of by variance as in Kernel Principal Components Analysis. In this work, we propose an extension of the KECA method, named Optimized KECA (OKECA), that directly extracts the optimal features retaining most of the data entropy by means of compacting the information in very few features (often in just one or two). The proposed method produces features which have higher expressive power. In particular, it is based on the Independent Component Analysis (ICA) framework, and introduces an extra rotation to the eigen-decomposition, which is optimized via gradient ascent search. This maximum entropy preservation suggests that OKECA features are more efficient than KECA features for density estimation. In addition, a critical issue in both methods is the selection of the kernel parameter since it critically affects the resulting performance. Here we analyze the most common kernel length-scale selection criteria. Results of both methods are illustrated in different synthetic and real problems. Results show that 1) OKECA returns projections with more expressive power than KECA, 2) the most successful rule for estimating the kernel parameter is based on maximum likelihood, and 3) OKECA is more robust to the selection of the length-scale parameter in kernel density estimation.