Hyperspherical Prototype Networks

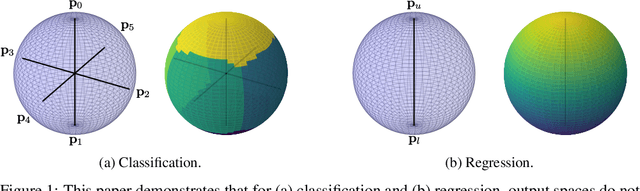
This paper introduces hyperspherical prototype networks, which unify regression and classification by prototypes on hyperspherical output spaces. Rather than defining prototypes as the mean output vector over training examples per class, we propose hyperspheres as output spaces to define class prototypes a priori with large margin separation. By doing so, we do not require any prototype updating, we can handle any training size, and the output dimensionality is no longer constrained to the number of classes. Furthermore, hyperspherical prototype networks generalize to regression, by optimizing outputs as an interpolation between two prototypes on the hypersphere. Since both tasks are now defined by the same loss function, they can be jointly optimized for multi-task problems. Experimental evaluation shows the benefits of hyperspherical prototype networks for classification, regression, and their combination.

Beyond Local Nash Equilibria for Adversarial Networks

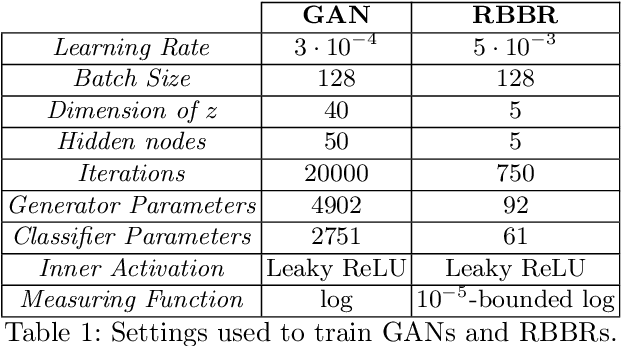
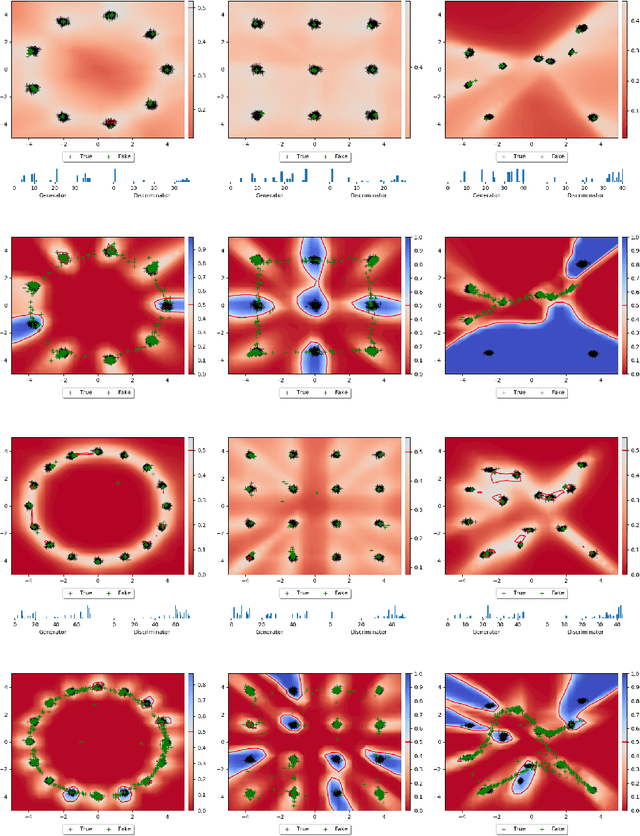
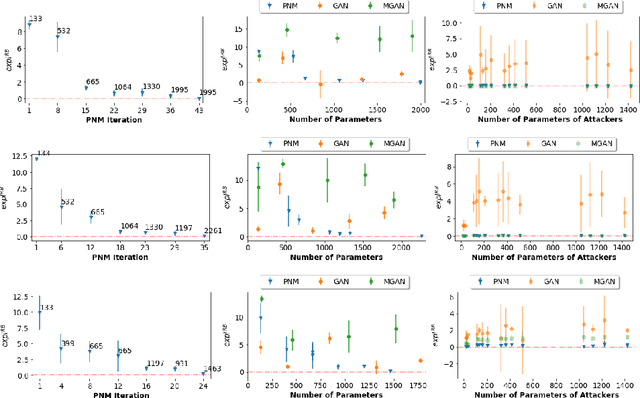
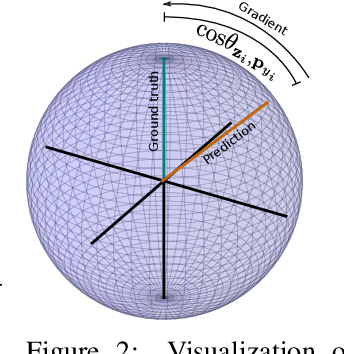
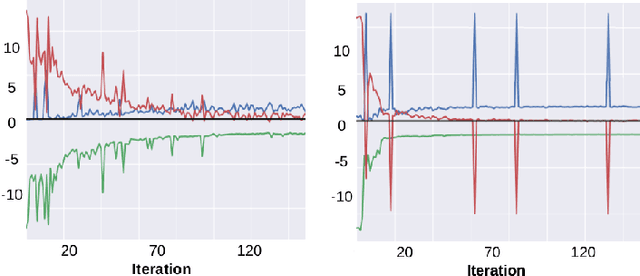
Save for some special cases, current training methods for Generative Adversarial Networks (GANs) are at best guaranteed to converge to a `local Nash equilibrium` (LNE). Such LNEs, however, can be arbitrarily far from an actual Nash equilibrium (NE), which implies that there are no guarantees on the quality of the found generator or classifier. This paper proposes to model GANs explicitly as finite games in mixed strategies, thereby ensuring that every LNE is an NE. With this formulation, we propose a solution method that is proven to monotonically converge to a resource-bounded Nash equilibrium (RB-NE): by increasing computational resources we can find better solutions. We empirically demonstrate that our method is less prone to typical GAN problems such as mode collapse, and produces solutions that are less exploitable than those produced by GANs and MGANs, and closely resemble theoretical predictions about NEs.

GANGs: Generative Adversarial Network Games

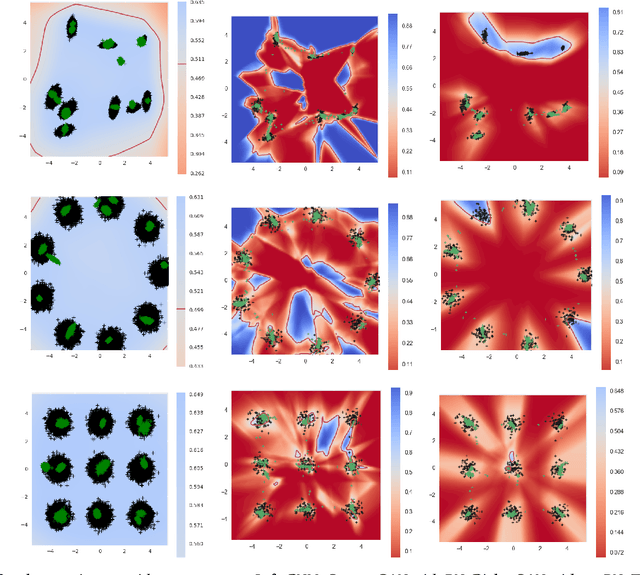
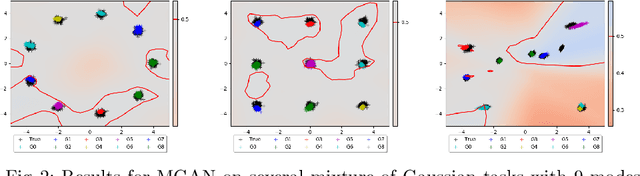
Generative Adversarial Networks (GAN) have become one of the most successful frameworks for unsupervised generative modeling. As GANs are difficult to train much research has focused on this. However, very little of this research has directly exploited game-theoretic techniques. We introduce Generative Adversarial Network Games (GANGs), which explicitly model a finite zero-sum game between a generator ($G$) and classifier ($C$) that use mixed strategies. The size of these games precludes exact solution methods, therefore we define resource-bounded best responses (RBBRs), and a resource-bounded Nash Equilibrium (RB-NE) as a pair of mixed strategies such that neither $G$ or $C$ can find a better RBBR. The RB-NE solution concept is richer than the notion of `local Nash equilibria' in that it captures not only failures of escaping local optima of gradient descent, but applies to any approximate best response computations, including methods with random restarts. To validate our approach, we solve GANGs with the Parallel Nash Memory algorithm, which provably monotonically converges to an RB-NE. We compare our results to standard GAN setups, and demonstrate that our method deals well with typical GAN problems such as mode collapse, partial mode coverage and forgetting.