Markovian Continuity of the MMSE

Minimum mean square error (MMSE) estimation is widely used in signal processing and related fields. While it is known to be non-continuous with respect to all standard notions of stochastic convergence, it remains robust in practical applications. In this work, we review the known counterexamples to the continuity of the MMSE. We observe that, in these counterexamples, the discontinuity arises from an element in the converging measurement sequence providing more information about the estimand than the limit of the measurement sequence. We argue that this behavior is uncharacteristic of real-world applications and introduce a new stochastic convergence notion, termed Markovian convergence, to address this issue. We prove that the MMSE is, in fact, continuous under this new notion. We supplement this result with semi-continuity and continuity guarantees of the MMSE in other settings and prove the continuity of the MMSE under linear estimation.

Regularized Classification-Aware Quantization

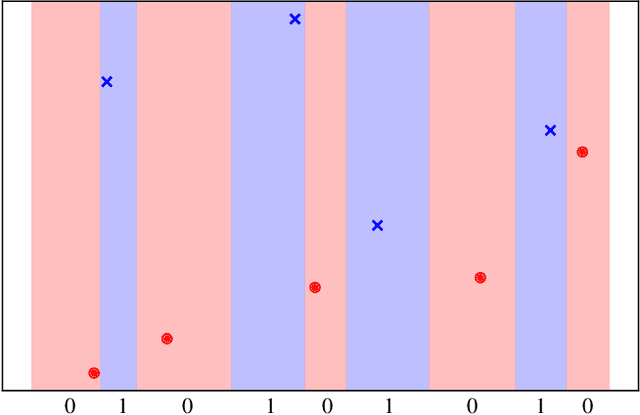
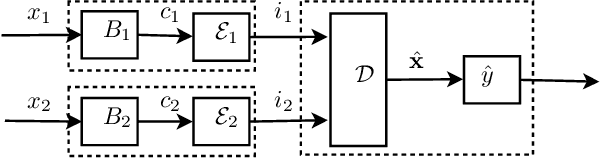
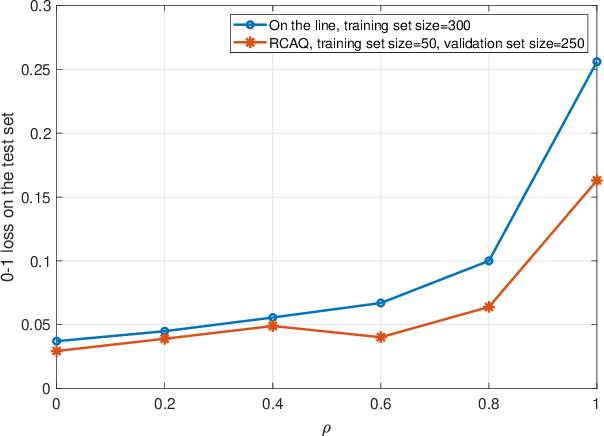
Traditionally, quantization is designed to minimize the reconstruction error of a data source. When considering downstream classification tasks, other measures of distortion can be of interest; such as the 0-1 classification loss. Furthermore, it is desirable that the performance of these quantizers not deteriorate once they are deployed into production, as relearning the scheme online is not always possible. In this work, we present a class of algorithms that learn distributed quantization schemes for binary classification tasks. Our method performs well on unseen data, and is faster than previous methods proportional to a quadratic term of the dataset size. It works by regularizing the 0-1 loss with the reconstruction error. We present experiments on synthetic mixture and bivariate Gaussian data and compare training, testing, and generalization errors with a family of benchmark quantization schemes from the literature. Our method is called Regularized Classification-Aware Quantization.