A Novel Update Mechanism for Q-Networks Based On Extreme Learning Machines

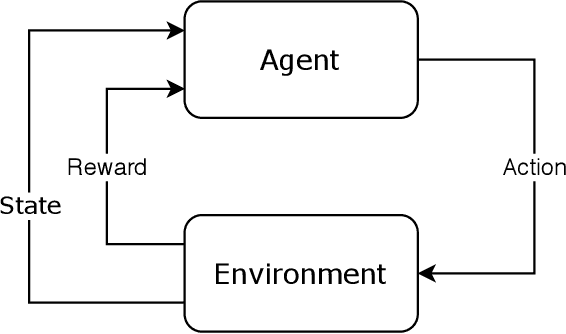
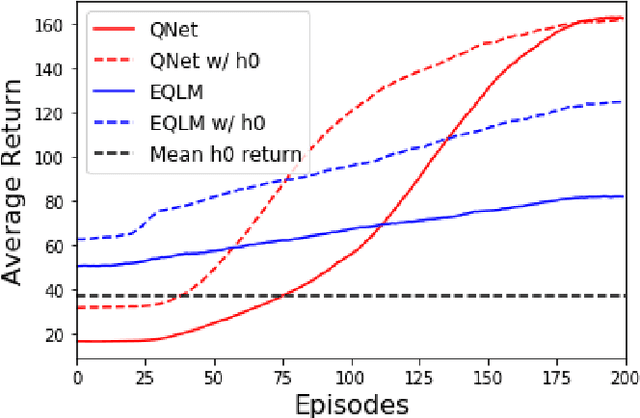
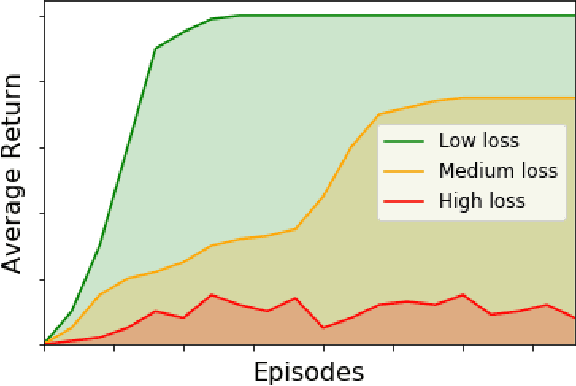
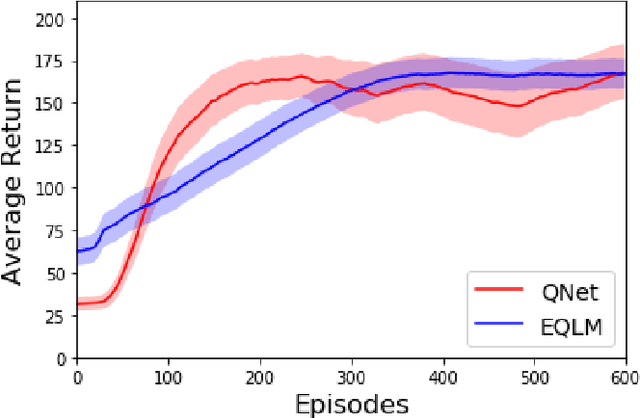
Reinforcement learning is a popular machine learning paradigm which can find near optimal solutions to complex problems. Most often, these procedures involve function approximation using neural networks with gradient based updates to optimise weights for the problem being considered. While this common approach generally works well, there are other update mechanisms which are largely unexplored in reinforcement learning. One such mechanism is Extreme Learning Machines. These were initially proposed to drastically improve the training speed of neural networks and have since seen many applications. Here we attempt to apply extreme learning machines to a reinforcement learning problem in the same manner as gradient based updates. This new algorithm is called Extreme Q-Learning Machine (EQLM). We compare its performance to a typical Q-Network on the cart-pole task - a benchmark reinforcement learning problem - and show EQLM has similar long-term learning performance to a Q-Network.

Approximated Computation of Belief Functions for Robust Design Optimization

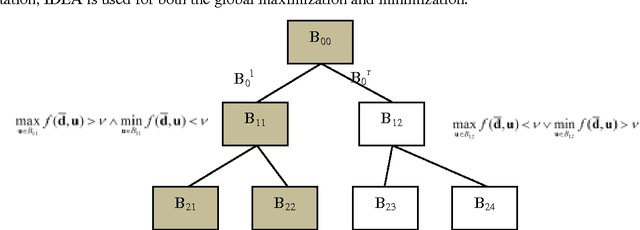
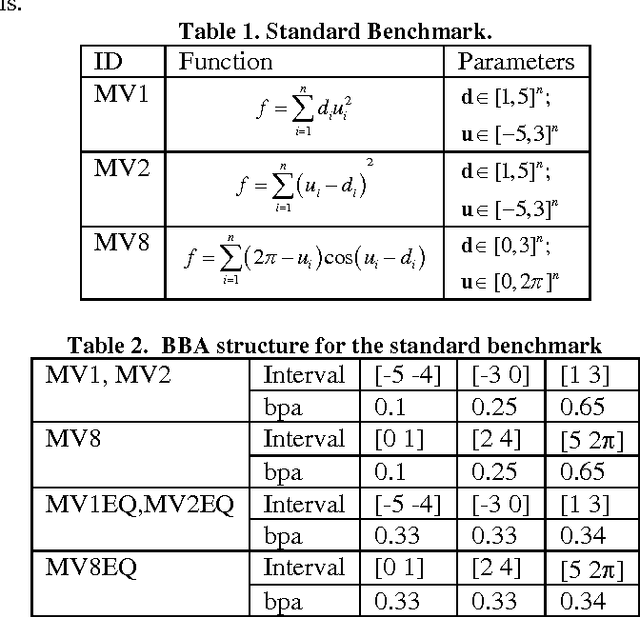
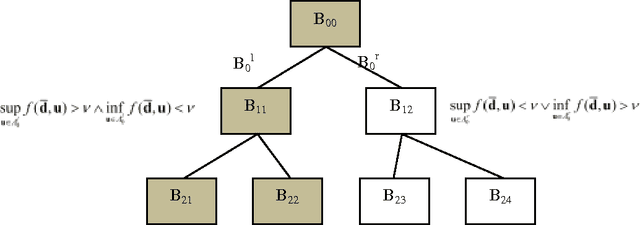
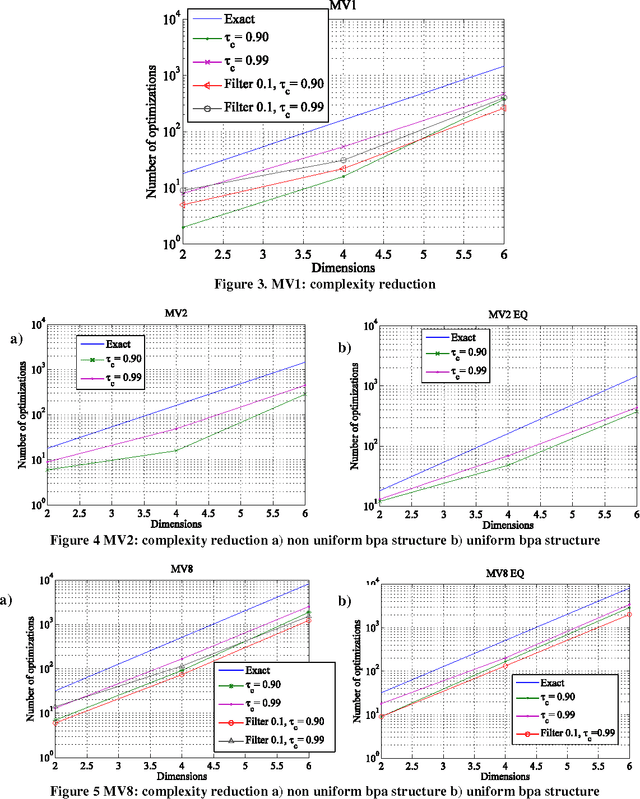
This paper presents some ideas to reduce the computational cost of evidence-based robust design optimization. Evidence Theory crystallizes both the aleatory and epistemic uncertainties in the design parameters, providing two quantitative measures, Belief and Plausibility, of the credibility of the computed value of the design budgets. The paper proposes some techniques to compute an approximation of Belief and Plausibility at a cost that is a fraction of the one required for an accurate calculation of the two values. Some simple test cases will show how the proposed techniques scale with the dimension of the problem. Finally a simple example of spacecraft system design is presented.

An inflationary differential evolution algorithm for space trajectory optimization

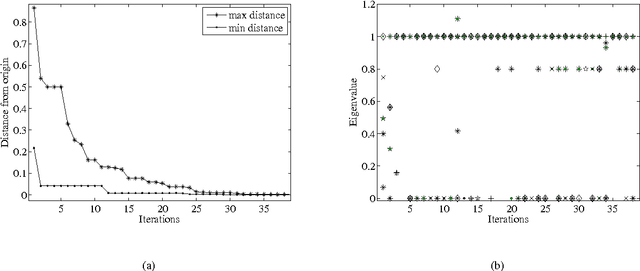
In this paper we define a discrete dynamical system that governs the evolution of a population of agents. From the dynamical system, a variant of Differential Evolution is derived. It is then demonstrated that, under some assumptions on the differential mutation strategy and on the local structure of the objective function, the proposed dynamical system has fixed points towards which it converges with probability one for an infinite number of generations. This property is used to derive an algorithm that performs better than standard Differential Evolution on some space trajectory optimization problems. The novel algorithm is then extended with a guided restart procedure that further increases the performance, reducing the probability of stagnation in deceptive local minima.