Topological comparison of some dimension reduction methods using persistent homology on EEG data

In this paper, we explore how to use topological tools to compare dimension reduction methods. We first make a brief overview of some of the methods often used dimension reduction such as Isometric Feature Mapping, Laplacian Eigenmaps, Fast Independent Component Analysis, Kernel Ridge Regression, t-distributed Stochastic Neighbor Embedding. We then give a brief overview of some topological notions used in topological data analysis, such as, barcodes, persistent homology, and Wasserstein distance. Theoretically, these methods applied on a data set can be interpreted differently. From EEG data embedded into a manifold of high dimension, we apply these methods and we compare them across persistent homologies of dimension 0, 1, and 2, that is, across connected components, tunnels and holes, shells around voids or cavities. We find that from three dimension clouds of points, it is not clear how distinct from each other the methods are, but Wasserstein and Bottleneck distances, topological tests of hypothesis, and various methods show that the methods qualitatively and significantly differ across homologies.

Analysis of EEG data using complex geometric structurization

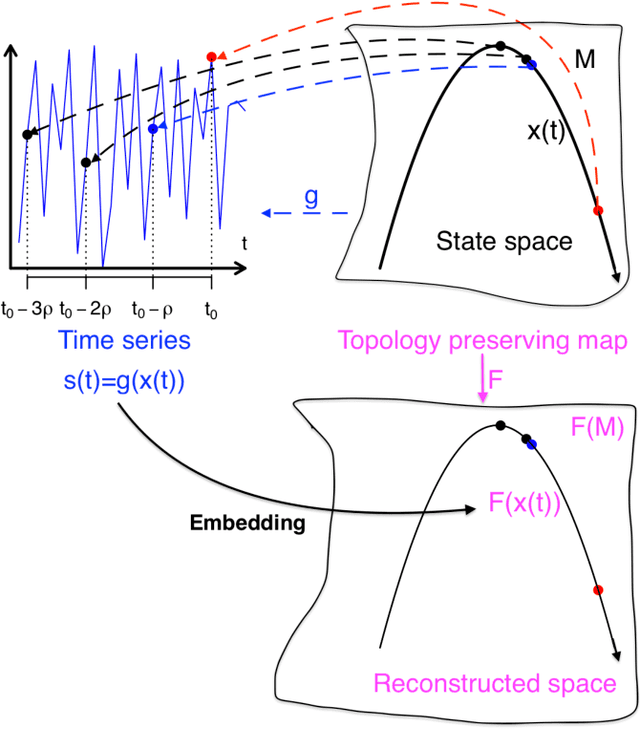
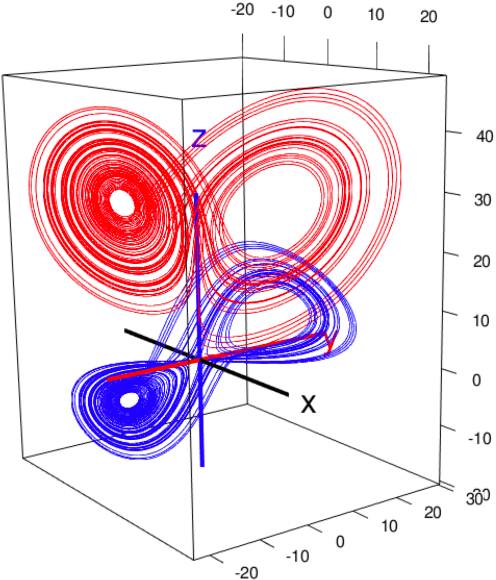
Electroencephalogram (EEG) is a common tool used to understand brain activities. The data are typically obtained by placing electrodes at the surface of the scalp and recording the oscillations of currents passing through the electrodes. These oscillations can sometimes lead to various interpretations, depending on the subject's health condition, the experiment carried out, the sensitivity of the tools used, human manipulations etc. The data obtained over time can be considered a time series. There is evidence in the literature that epilepsy EEG data may be chaotic. Either way, the embedding theory in dynamical systems suggests that time series from a complex system could be used to reconstruct its phase space under proper conditions. In this paper, we propose an analysis of epilepsy electroencephalogram time series data based on a novel approach dubbed complex geometric structurization. Complex geometric structurization stems from the construction of strange attractors using embedding theory from dynamical systems. The complex geometric structures are themselves obtained using a geometry tool, namely the $\alpha$-shapes from shape analysis. Initial analyses show a proof of concept in that these complex structures capture the expected changes brain in lobes under consideration. Further, a deeper analysis suggests that these complex structures can be used as biomarkers for seizure changes.