SAFE: Finding Sparse and Flat Minima to Improve Pruning

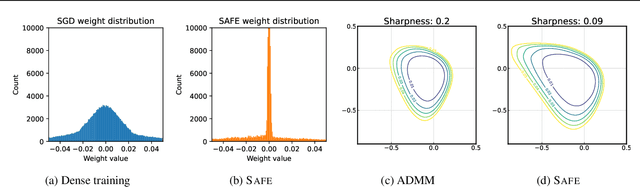
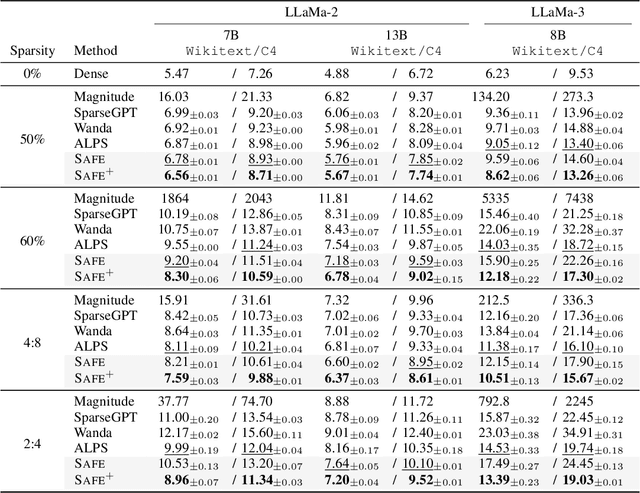
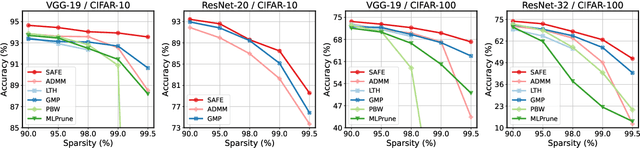
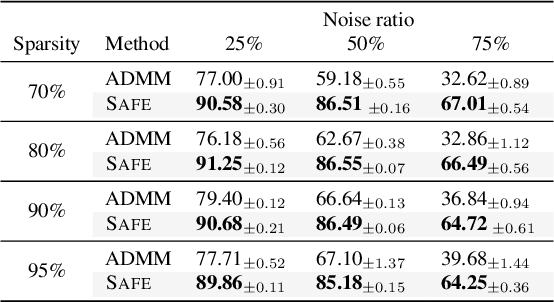
Sparsifying neural networks often suffers from seemingly inevitable performance degradation, and it remains challenging to restore the original performance despite much recent progress. Motivated by recent studies in robust optimization, we aim to tackle this problem by finding subnetworks that are both sparse and flat at the same time. Specifically, we formulate pruning as a sparsity-constrained optimization problem where flatness is encouraged as an objective. We solve it explicitly via an augmented Lagrange dual approach and extend it further by proposing a generalized projection operation, resulting in novel pruning methods called SAFE and its extension, SAFE$^+$. Extensive evaluations on standard image classification and language modeling tasks reveal that SAFE consistently yields sparse networks with improved generalization performance, which compares competitively to well-established baselines. In addition, SAFE demonstrates resilience to noisy data, making it well-suited for real-world conditions.

SASSHA: Sharpness-aware Adaptive Second-order Optimization with Stable Hessian Approximation

Approximate second-order optimization methods often exhibit poorer generalization compared to first-order approaches. In this work, we look into this issue through the lens of the loss landscape and find that existing second-order methods tend to converge to sharper minima compared to SGD. In response, we propose Sassha, a novel second-order method designed to enhance generalization by explicitly reducing sharpness of the solution, while stabilizing the computation of approximate Hessians along the optimization trajectory. In fact, this sharpness minimization scheme is crafted also to accommodate lazy Hessian updates, so as to secure efficiency besides flatness. To validate its effectiveness, we conduct a wide range of standard deep learning experiments where Sassha demonstrates its outstanding generalization performance that is comparable to, and mostly better than, other methods. We provide a comprehensive set of analyses including convergence, robustness, stability, efficiency, and cost.

The Effects of Overparameterization on Sharpness-aware Minimization: An Empirical and Theoretical Analysis

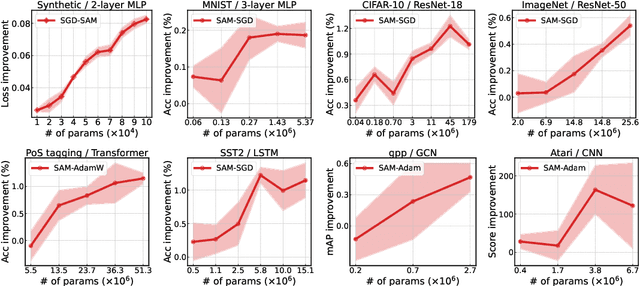
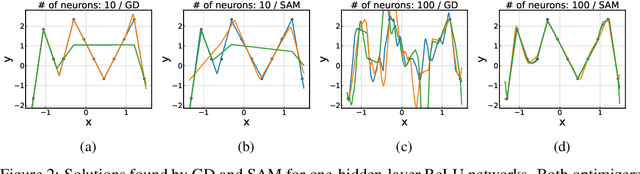
Training an overparameterized neural network can yield minimizers of the same level of training loss and yet different generalization capabilities. With evidence that indicates a correlation between sharpness of minima and their generalization errors, increasing efforts have been made to develop an optimization method to explicitly find flat minima as more generalizable solutions. This sharpness-aware minimization (SAM) strategy, however, has not been studied much yet as to how overparameterization can actually affect its behavior. In this work, we analyze SAM under varying degrees of overparameterization and present both empirical and theoretical results that suggest a critical influence of overparameterization on SAM. Specifically, we first use standard techniques in optimization to prove that SAM can achieve a linear convergence rate under overparameterization in a stochastic setting. We also show that the linearly stable minima found by SAM are indeed flatter and have more uniformly distributed Hessian moments compared to those of SGD. These results are corroborated with our experiments that reveal a consistent trend that the generalization improvement made by SAM continues to increase as the model becomes more overparameterized. We further present that sparsity can open up an avenue for effective overparameterization in practice.