Donald A Adjeroh
Generative Probabilistic Novelty Detection with Adversarial Autoencoders
Jul 06, 2018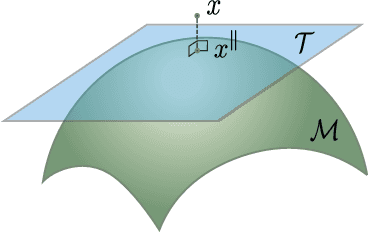
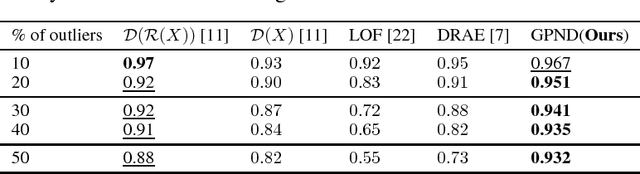
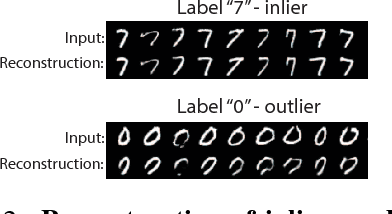
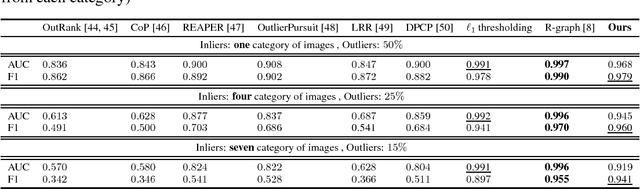
Abstract:Novelty detection is the problem of identifying whether a new data point is considered to be an inlier or an outlier. We assume that training data is available to describe only the inlier distribution. Recent approaches primarily leverage deep encoder-decoder network architectures to compute a reconstruction error that is used to either compute a novelty score or to train a one-class classifier. While we too leverage a novel network of that kind, we take a probabilistic approach and effectively compute how likely is that a sample was generated by the inlier distribution. We achieve this with two main contributions. First, we make the computation of the novelty probability feasible because we linearize the parameterized manifold capturing the underlying structure of the inlier distribution, and show how the probability factorizes and can be computed with respect to local coordinates of the manifold tangent space. Second, we improved the training of the autoencoder network. An extensive set of results show that the approach achieves state-of-the-art results on several benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge