CATNet: A geometric deep learning approach for CAT bond spread prediction in the primary market

Traditional models for pricing catastrophe (CAT) bonds struggle to capture the complex, relational data inherent in these instruments. This paper introduces CATNet, a novel framework that applies a geometric deep learning architecture, the Relational Graph Convolutional Network (R-GCN), to model the CAT bond primary market as a graph, leveraging its underlying network structure for spread prediction. Our analysis reveals that the CAT bond market exhibits the characteristics of a scale-free network, a structure dominated by a few highly connected and influential hubs. CATNet demonstrates high predictive performance, significantly outperforming a strong Random Forest benchmark. The inclusion of topological centrality measures as features provides a further, significant boost in accuracy. Interpretability analysis confirms that these network features are not mere statistical artifacts; they are quantitative proxies for long-held industry intuition regarding issuer reputation, underwriter influence, and peril concentration. This research provides evidence that network connectivity is a key determinant of price, offering a new paradigm for risk assessment and proving that graph-based models can deliver both state-of-the-art accuracy and deeper, quantifiable market insights.

A Unified Bayesian Framework for Pricing Catastrophe Bond Derivatives

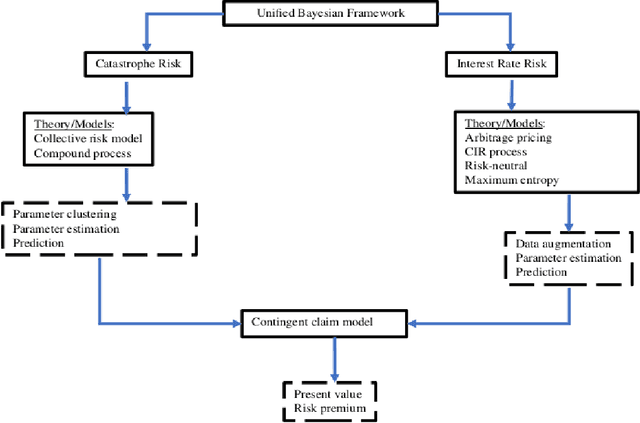
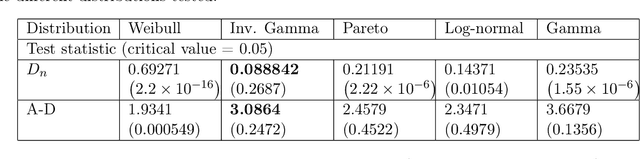
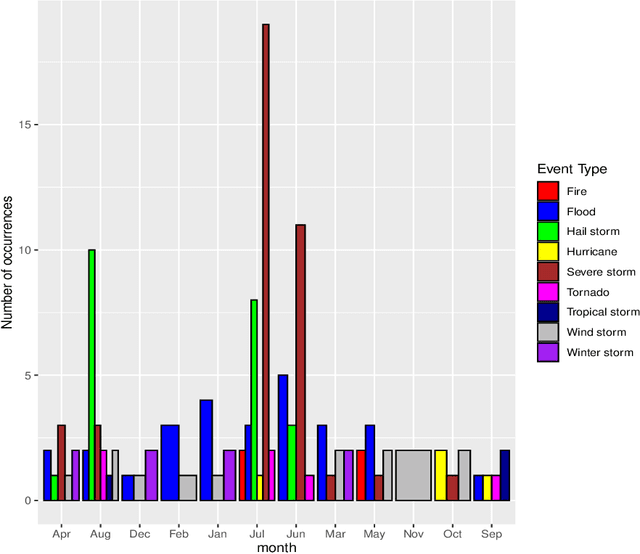
Catastrophe (CAT) bond markets are incomplete and hence carry uncertainty in instrument pricing. As such various pricing approaches have been proposed, but none treat the uncertainty in catastrophe occurrences and interest rates in a sufficiently flexible and statistically reliable way within a unifying asset pricing framework. Consequently, little is known empirically about the expected risk-premia of CAT bonds. The primary contribution of this paper is to present a unified Bayesian CAT bond pricing framework based on uncertainty quantification of catastrophes and interest rates. Our framework allows for complex beliefs about catastrophe risks to capture the distinct and common patterns in catastrophe occurrences, and when combined with stochastic interest rates, yields a unified asset pricing approach with informative expected risk premia. Specifically, using a modified collective risk model -- Dirichlet Prior-Hierarchical Bayesian Collective Risk Model (DP-HBCRM) framework -- we model catastrophe risk via a model-based clustering approach. Interest rate risk is modeled as a CIR process under the Bayesian approach. As a consequence of casting CAT pricing models into our framework, we evaluate the price and expected risk premia of various CAT bond contracts corresponding to clustering of catastrophe risk profiles. Numerical experiments show how these clusters reveal how CAT bond prices and expected risk premia relate to claim frequency and loss severity.