Dimitris N. Politis
Deep Limit Model-free Prediction in Regression
Aug 18, 2024Abstract:In this paper, we provide a novel Model-free approach based on Deep Neural Network (DNN) to accomplish point prediction and prediction interval under a general regression setting. Usually, people rely on parametric or non-parametric models to bridge dependent and independent variables (Y and X). However, this classical method relies heavily on the correct model specification. Even for the non-parametric approach, some additive form is often assumed. A newly proposed Model-free prediction principle sheds light on a prediction procedure without any model assumption. Previous work regarding this principle has shown better performance than other standard alternatives. Recently, DNN, one of the machine learning methods, has received increasing attention due to its great performance in practice. Guided by the Model-free prediction idea, we attempt to apply a fully connected forward DNN to map X and some appropriate reference random variable Z to Y. The targeted DNN is trained by minimizing a specially designed loss function so that the randomness of Y conditional on X is outsourced to Z through the trained DNN. Our method is more stable and accurate compared to other DNN-based counterparts, especially for optimal point predictions. With a specific prediction procedure, our prediction interval can capture the estimation variability so that it can render a better coverage rate for finite sample cases. The superior performance of our method is verified by simulation and empirical studies.
Scalable Subsampling Inference for Deep Neural Networks
May 14, 2024Abstract:Deep neural networks (DNN) has received increasing attention in machine learning applications in the last several years. Recently, a non-asymptotic error bound has been developed to measure the performance of the fully connected DNN estimator with ReLU activation functions for estimating regression models. The paper at hand gives a small improvement on the current error bound based on the latest results on the approximation ability of DNN. More importantly, however, a non-random subsampling technique--scalable subsampling--is applied to construct a `subagged' DNN estimator. Under regularity conditions, it is shown that the subagged DNN estimator is computationally efficient without sacrificing accuracy for either estimation or prediction tasks. Beyond point estimation/prediction, we propose different approaches to build confidence and prediction intervals based on the subagged DNN estimator. In addition to being asymptotically valid, the proposed confidence/prediction intervals appear to work well in finite samples. All in all, the scalable subsampling DNN estimator offers the complete package in terms of statistical inference, i.e., (a) computational efficiency; (b) point estimation/prediction accuracy; and (c) allowing for the construction of practically useful confidence and prediction intervals.
Ridge Regression Revisited: Debiasing, Thresholding and Bootstrap
Sep 17, 2020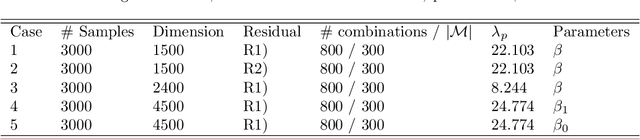
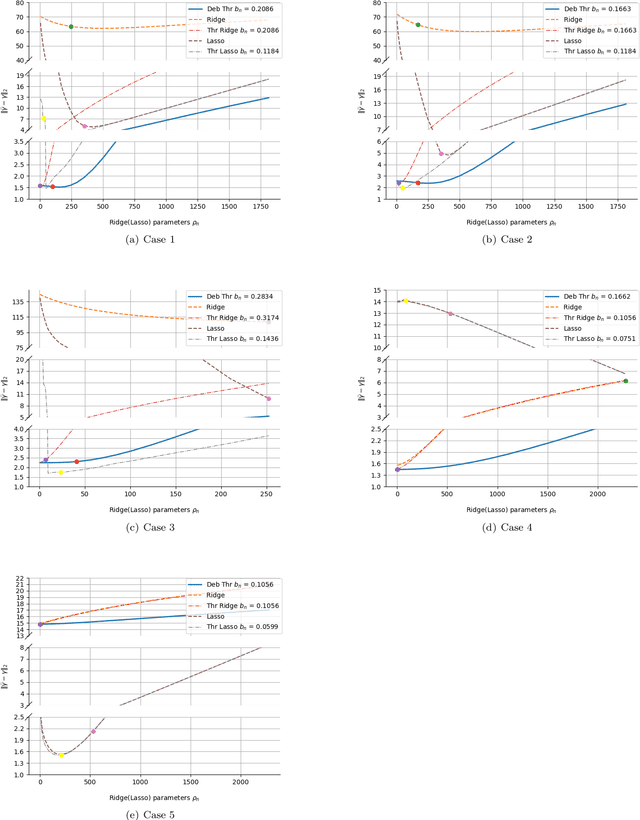

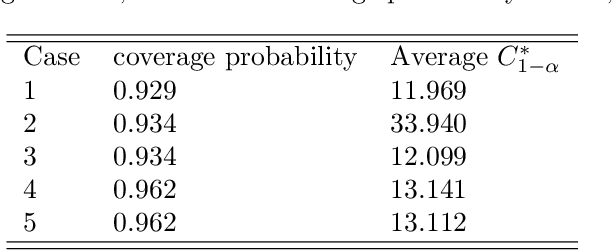
Abstract:In high dimensional setting, the facts that the classical ridge regression method cannot perform model selection on its own and it introduces large bias make this method an unsatisfactory tool for analyzing high dimensional linear models. In this paper, we propose the debiased and threshold ridge regression method which solves these drawbacks. Besides, focus on performing statistical inference and prediction of linear combinations of parameters, we provide a normal approximation theorem for the estimator and propose two bootstrap algorithms which provide joint confidence regions and prediction regions for the linear combinations. In statistical inference part, apart from the dimension of parameters, we allow the number of linear combinations to grow as sample size increases. From numerical experiments, we can see that the proposed regression method is robust with the fluctuation in ridge parameter and reduces estimation errors compared to classical and threshold ridge regression methods. Apart from theoretical interests, the proposed algorithms can be applied to disciplines such as econometrics, biology and etc.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge