Multi-robot Symmetric Rendezvous Search on the Line

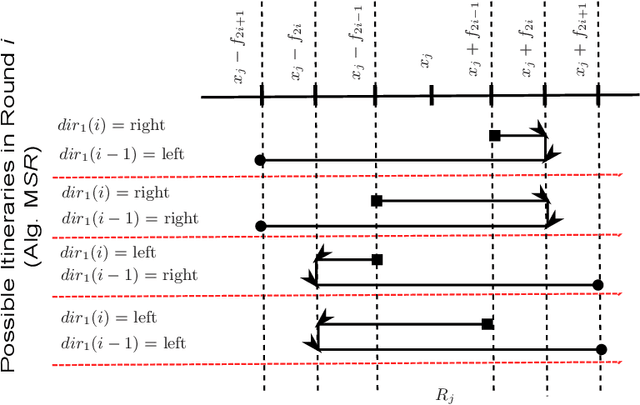
We study the Symmetric Rendezvous Search Problem for a multi-robot system. There are $n>2$ robots arbitrarily located on a line. Their goal is to meet somewhere on the line as quickly as possible. The robots do not know the initial location of any of the other robots or their own positions on the line. The symmetric version of the problem requires the robots to execute the same search strategy to achieve rendezvous. Therefore, we solve the problem in an online fashion with a randomized strategy. In this paper, we present a symmetric rendezvous algorithm which achieves a constant competitive ratio for the total distance traveled by the robots. We validate our theoretical results through simulations.

Multi-robot Symmetric Rendezvous Search on the Line with an Unknown Initial Distance

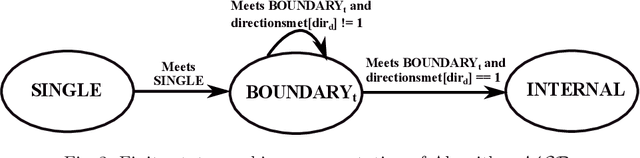
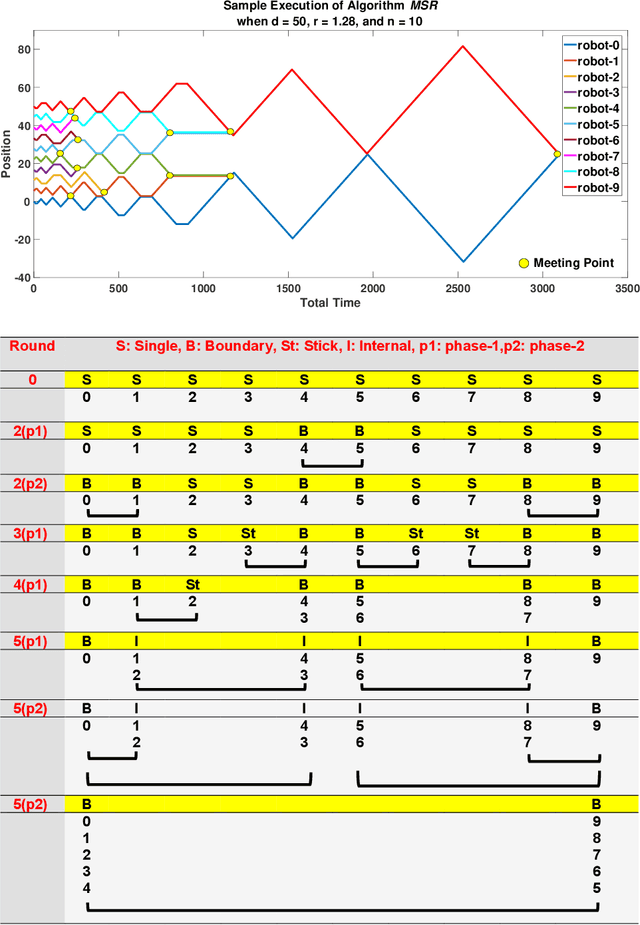
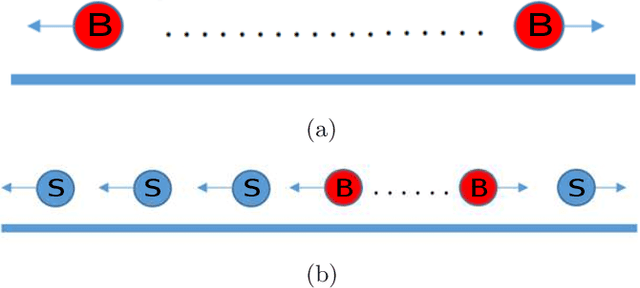
In this paper, we study the symmetric rendezvous search problem on the line with n > 2 robots that are unaware of their locations and the initial distances between them. In the symmetric version of this problem, the robots execute the same strategy. The multi-robot symmetric rendezvous algorithm, MSR presented in this paper is an extension our symmetric rendezvous algorithm, SR presented in [23]. We study both the synchronous and asynchronous cases of the problem. The asynchronous version of MSR algorithm is called MASR algorithm. We consider that robots start executing MASR at different times. We perform the theoretical analysis of MSR and MASR, and show that their competitive ratios are $O(n^{0.67})$ and $O(n^{1.5})$, respectively. Finally, we confirm our theoretical results through simulations.