Fast $k$-means clustering in Riemannian manifolds via Fréchet maps: Applications to large-dimensional SPD matrices

We introduce a novel, efficient framework for clustering data on high-dimensional, non-Euclidean manifolds that overcomes the computational challenges associated with standard intrinsic methods. The key innovation is the use of the $p$-Fréchet map $F^p : \mathcal{M} \to \mathbb{R}^\ell$ -- defined on a generic metric space $\mathcal{M}$ -- which embeds the manifold data into a lower-dimensional Euclidean space $\mathbb{R}^\ell$ using a set of reference points $\{r_i\}_{i=1}^\ell$, $r_i \in \mathcal{M}$. Once embedded, we can efficiently and accurately apply standard Euclidean clustering techniques such as k-means. We rigorously analyze the mathematical properties of $F^p$ in the Euclidean space and the challenging manifold of $n \times n$ symmetric positive definite matrices $\mathit{SPD}(n)$. Extensive numerical experiments using synthetic and real $\mathit{SPD}(n)$ data demonstrate significant performance gains: our method reduces runtime by up to two orders of magnitude compared to intrinsic manifold-based approaches, all while maintaining high clustering accuracy, including scenarios where existing alternative methods struggle or fail.

Blind Image Inpainting with Sparse Directional Filter Dictionaries for Lightweight CNNs

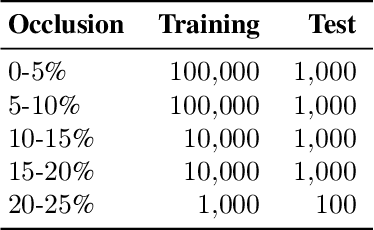
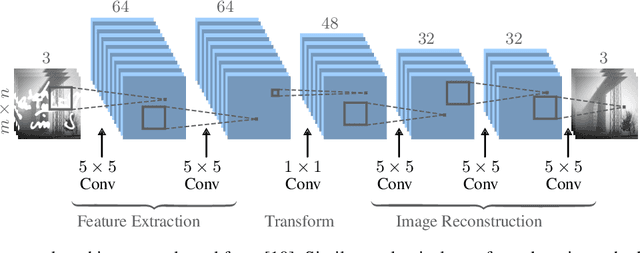
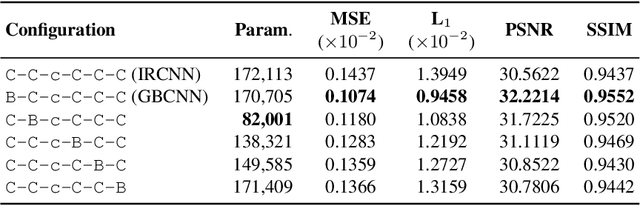
Blind inpainting algorithms based on deep learning architectures have shown a remarkable performance in recent years, typically outperforming model-based methods both in terms of image quality and run time. However, neural network strategies typically lack a theoretical explanation, which contrasts with the well-understood theory underlying model-based methods. In this work, we leverage the advantages of both approaches by integrating theoretically founded concepts from transform domain methods and sparse approximations into a CNN-based approach for blind image inpainting. To this end, we present a novel strategy to learn convolutional kernels that applies a specifically designed filter dictionary whose elements are linearly combined with trainable weights. Numerical experiments demonstrate the competitiveness of this approach. Our results show not only an improved inpainting quality compared to conventional CNNs but also significantly faster network convergence within a lightweight network design.