Tensor Completion via Monotone Inclusion: Generalized Low-Rank Priors Meet Deep Denoisers

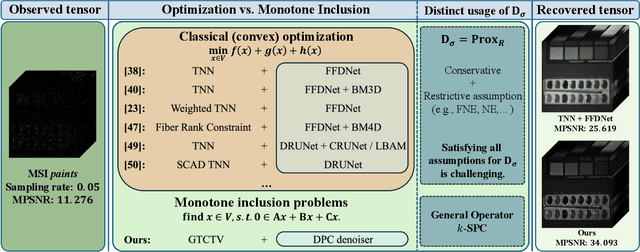
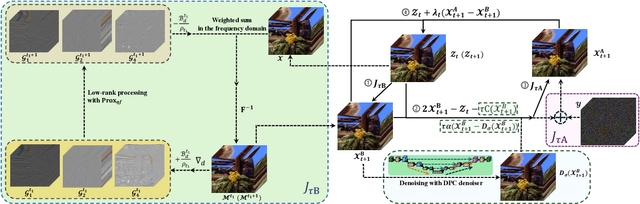
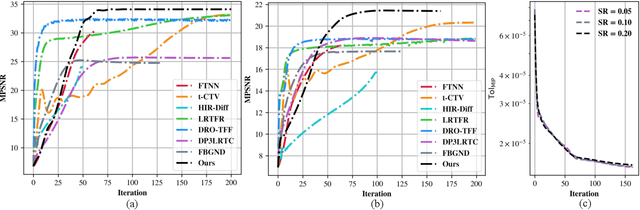
Missing entries in multi dimensional data pose significant challenges for downstream analysis across diverse real world applications. These data are naturally modeled as tensors, and recent completion methods integrating global low rank priors with plug and play denoisers have demonstrated strong empirical performance. However, these approaches often rely on empirical convergence alone or unrealistic assumptions, such as deep denoisers acting as proximal operators of implicit regularizers, which generally does not hold. To address these limitations, we propose a novel tensor completion framework grounded in the monotone inclusion paradigm, which unifies generalized low rank priors with deep pseudo contractive denoisers and extends beyond traditional convex optimization. Building on the Davis Yin splitting scheme, we develop the GTCTV DPC algorithm and rigorously establish its global convergence. Extensive experiments demonstrate that GTCTV DPC consistently outperforms existing methods in both quantitative metrics and visual quality, particularly at low sampling rates.

Learning Cocoercive Conservative Denoisers via Helmholtz Decomposition for Poisson Inverse Problems

Plug-and-play (PnP) methods with deep denoisers have shown impressive results in imaging problems. They typically require strong convexity or smoothness of the fidelity term and a (residual) non-expansive denoiser for convergence. These assumptions, however, are violated in Poisson inverse problems, and non-expansiveness can hinder denoising performance. To address these challenges, we propose a cocoercive conservative (CoCo) denoiser, which may be (residual) expansive, leading to improved denoising. By leveraging the generalized Helmholtz decomposition, we introduce a novel training strategy that combines Hamiltonian regularization to promote conservativeness and spectral regularization to ensure cocoerciveness. We prove that CoCo denoiser is a proximal operator of a weakly convex function, enabling a restoration model with an implicit weakly convex prior. The global convergence of PnP methods to a stationary point of this restoration model is established. Extensive experimental results demonstrate that our approach outperforms closely related methods in both visual quality and quantitative metrics.

Learning pseudo-contractive denoisers for inverse problems

Deep denoisers have shown excellent performance in solving inverse problems in signal and image processing. In order to guarantee the convergence, the denoiser needs to satisfy some Lipschitz conditions like non-expansiveness. However, enforcing such constraints inevitably compromises recovery performance. This paper introduces a novel training strategy that enforces a weaker constraint on the deep denoiser called pseudo-contractiveness. By studying the spectrum of the Jacobian matrix, relationships between different denoiser assumptions are revealed. Effective algorithms based on gradient descent and Ishikawa process are derived, and further assumptions of strict pseudo-contractiveness yield efficient algorithms using half-quadratic splitting and forward-backward splitting. The proposed algorithms theoretically converge strongly to a fixed point. A training strategy based on holomorphic transformation and functional calculi is proposed to enforce the pseudo-contractive denoiser assumption. Extensive experiments demonstrate superior performance of the pseudo-contractive denoiser compared to related denoisers. The proposed methods are competitive in terms of visual effects and quantitative values.