Time-to-event regression using partially monotonic neural networks

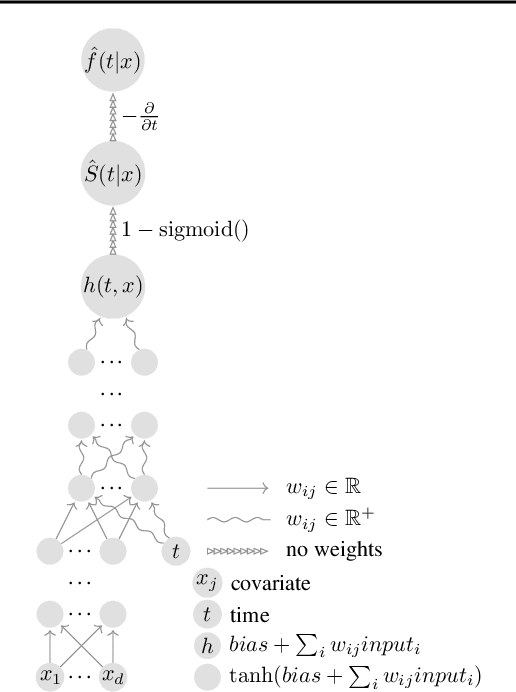
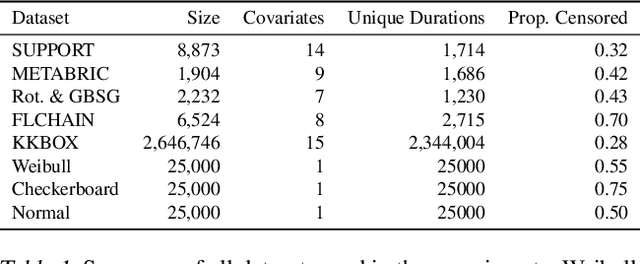
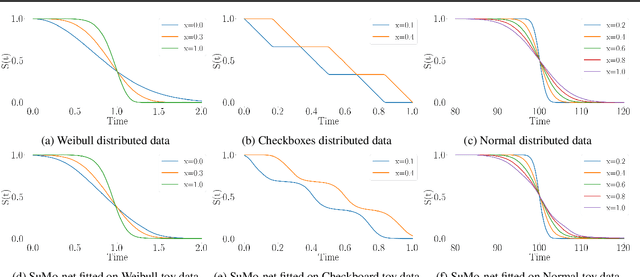
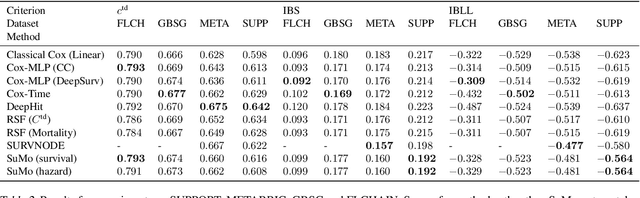
We propose a novel method, termed SuMo-net, that uses partially monotonic neural networks to learn a time-to-event distribution from a sample of covariates and right-censored times. SuMo-net models the survival function and the density jointly, and optimizes the likelihood for right-censored data instead of the often used partial likelihood. The method does not make assumptions about the true survival distribution and avoids computationally expensive integration of the hazard function. We evaluate the performance of the method on a range of datasets and find competitive performance across different metrics and improved computational time of making new predictions.

A kernel log-rank test of independence for right-censored data

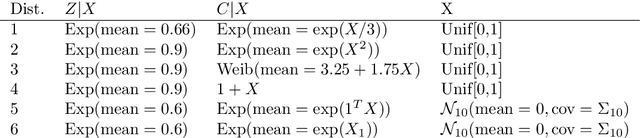
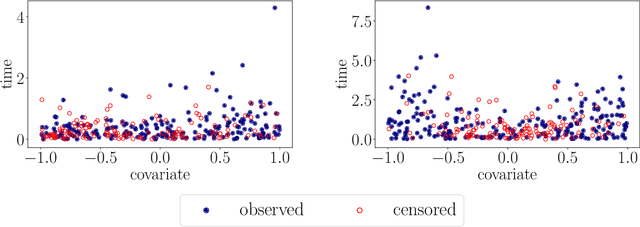
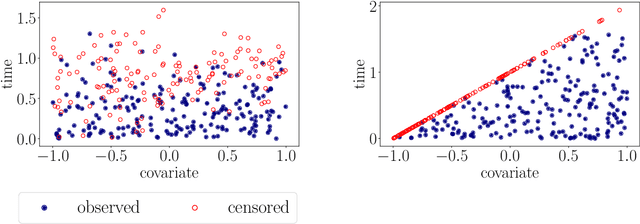
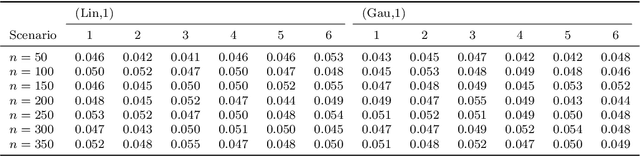
With the incorporation of new data gathering methods in clinical research, it becomes fundamental for survival analysis techniques to deal with high-dimensional or/and non-standard covariates. In this paper we introduce a general non-parametric independence test between right-censored survival times and covariates taking values on a general (not necessarily Euclidean) space $\mathcal{X}$. We show that our test statistic has a dual interpretation, first in terms of the supremum of a potentially infinite collection of weight-indexed log-rank tests, with weight functions belonging to a reproducing kernel Hilbert space (RKHS) of functions; and second, as the norm of the difference of embeddings of certain finite measures into the RKHS, similar to the Hilbert-Schmidt Independence Criterion (HSIC) test-statistic. We study the asymptotic properties of the test, finding sufficient conditions to ensure that our test is omnibus. The test statistic can be computed straightforwardly, and the rejection threshold is obtained via an asymptotically consistent Wild-Bootstrap procedure. We perform extensive simulations demonstrating that our testing procedure generally performs better than competing approaches in detecting complex nonlinear dependence.

Nonparametric Independence Testing for Right-Censored Data using Optimal Transport

We propose a nonparametric test of independence, termed OPT-HSIC, between a covariate and a right-censored lifetime. Because the presence of censoring creates a challenge in applying the standard permutation-based testing approaches, we use optimal transport to transform the censored dataset into an uncensored one, while preserving the relevant dependencies. We then apply a permutation test using the kernel-based dependence measure as a statistic to the transformed dataset. The type 1 error is proven to be correct in the case where censoring is independent of the covariate. Experiments indicate that OPT-HSIC has power against a much wider class of alternatives than Cox proportional hazards regression and that it has the correct type 1 control even in the challenging cases where censoring strongly depends on the covariate.