Classifiers in High Dimensional Hilbert Metrics

Classifying points in high dimensional spaces is a fundamental geometric problem in machine learning. In this paper, we address classifying points in the $d$-dimensional Hilbert polygonal metric. The Hilbert metric is a generalization of the Cayley-Klein hyperbolic distance to arbitrary convex bodies and has a diverse range of applications in machine learning and convex geometry. We first present an efficient LP-based algorithm in the metric for the large-margin SVM problem. Our algorithm runs in time polynomial to the number of points, bounding facets, and dimension. This is a significant improvement on previous works, which either provide no theoretical guarantees on running time, or suffer from exponential runtime. We also consider the closely related Funk metric. We also present efficient algorithms for the soft-margin SVM problem and for nearest neighbor-based classification in the Hilbert metric.

Coresets for the Nearest-Neighbor Rule

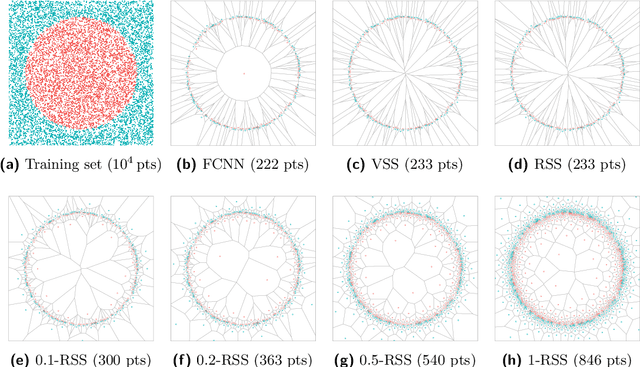
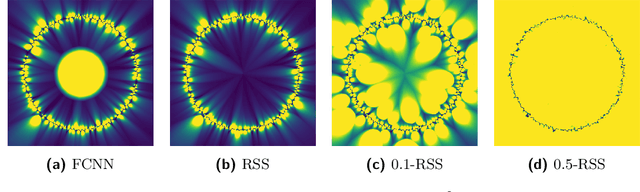
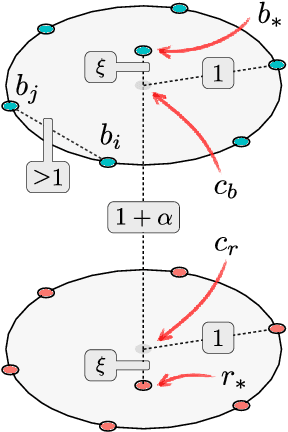
The problem of nearest-neighbor condensation deals with finding a subset $R$ from a set of labeled points $P$ such that for every point $p \in P$ the nearest-neighbor of $p$ in $R$ has the same label as $p$. This is motivated by applications in classification, where the nearest-neighbor rule assigns to an unlabeled query point the label of its nearest-neighbor in the point set. In this context, condensation aims to reduce the size of the set needed to classify new points. However, finding such subsets of minimum cardinality is NP-hard, and most research has focused on practical heuristics without performance guarantees. Additionally, the use of exact nearest-neighbors is always assumed, ignoring the effect of condensation in the classification accuracy when nearest-neighbors are computed approximately. In this paper, we address these shortcomings by proposing new approximation-sensitive criteria for the nearest-neighbor condensation problem, along with practical algorithms with provable performance guarantees. We characterize sufficient conditions to guarantee correct classification of unlabeled points using approximate nearest-neighbor queries on these subsets, which introduces the notion of coresets for classification with the nearest-neighbor rule. Moreover, we prove that it is NP-hard to compute subsets with these characteristics, whose cardinality approximates that of the minimum cardinality subset. Additionally, we propose new algorithms for computing such subsets, with tight approximation factors in general metrics, and improved factors for doubling metrics and $\ell_p$ metrics with $p\geq2$. Finally, we show an alternative implementation scheme that reduces the worst-case time complexity of one of these algorithms, becoming the first truly subquadratic approximation algorithm for the nearest-neighbor condensation problem.