The WQN algorithm for EEG artifact removal in the absence of scale invariance

Electroencephalogram (EEG) signals reflect brain activity across different brain states, characterized by distinct frequency distributions. Through multifractal analysis tools, we investigate the scaling behaviour of different classes of EEG signals and artifacts. We show that brain states associated to sleep and general anaesthesia are not in general characterized by scale invariance. The lack of scale invariance motivates the development of artifact removal algorithms capable of operating independently at each scale. We examine here the properties of the wavelet quantile normalization algorithm, a recently introduced adaptive method for real-time correction of transient artifacts in EEG signals. We establish general results regarding the regularization properties of the WQN algorithm, showing how it can eliminate singularities introduced by artefacts, and we compare it to traditional thresholding algorithms. Furthermore, we show that the algorithm performance is independent of the wavelet basis. We finally examine its continuity and boundedness properties and illustrate its distinctive non-local action on the wavelet coefficients through pathological examples.

The WQN algorithm to adaptively correct artifacts in the EEG signal

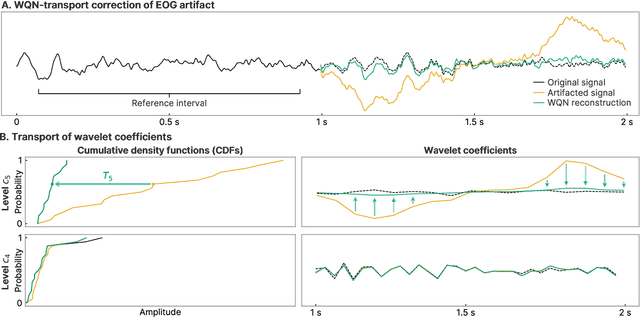
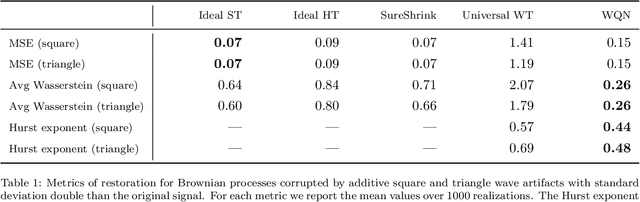
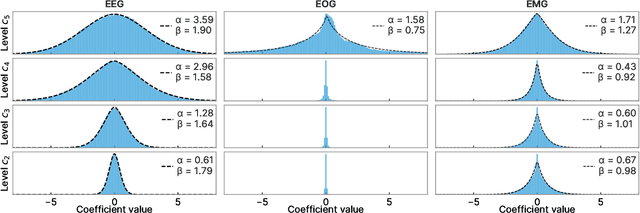
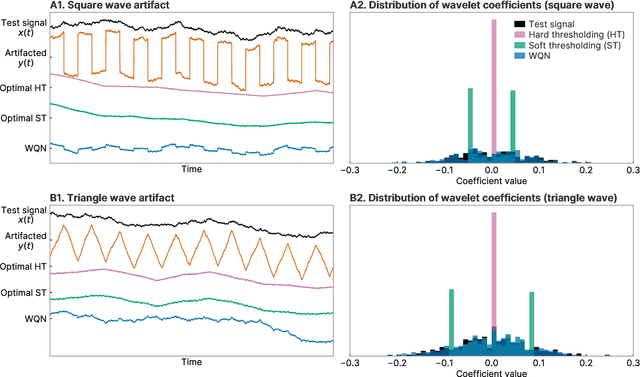
Wavelet quantile normalization (WQN) is a nonparametric algorithm designed to efficiently remove transient artifacts from single-channel EEG in real-time clinical monitoring. Today, EEG monitoring machines suspend their output when artifacts in the signal are detected. Removing unpredictable EEG artifacts would thus allow to improve the continuity of the monitoring. We analyze the WQN algorithm which consists in transporting wavelet coefficient distributions of an artifacted epoch into a reference, uncontaminated signal distribution. We show that the algorithm regularizes the signal. To confirm that the algorithm is well suited, we study the empirical distributions of the EEG and the artifacts wavelet coefficients. We compare the WQN algorithm to the classical wavelet thresholding methods and study their effect on the distribution of the wavelet coefficients. We show that the WQN algorithm preserves the distribution while the thresholding methods can cause alterations. Finally, we show how the spectrogram computed from an EEG signal can be cleaned using the WQN algorithm.