Machine-Learning Driven Load Shedding to Mitigate Instability Attacks in Power Grids

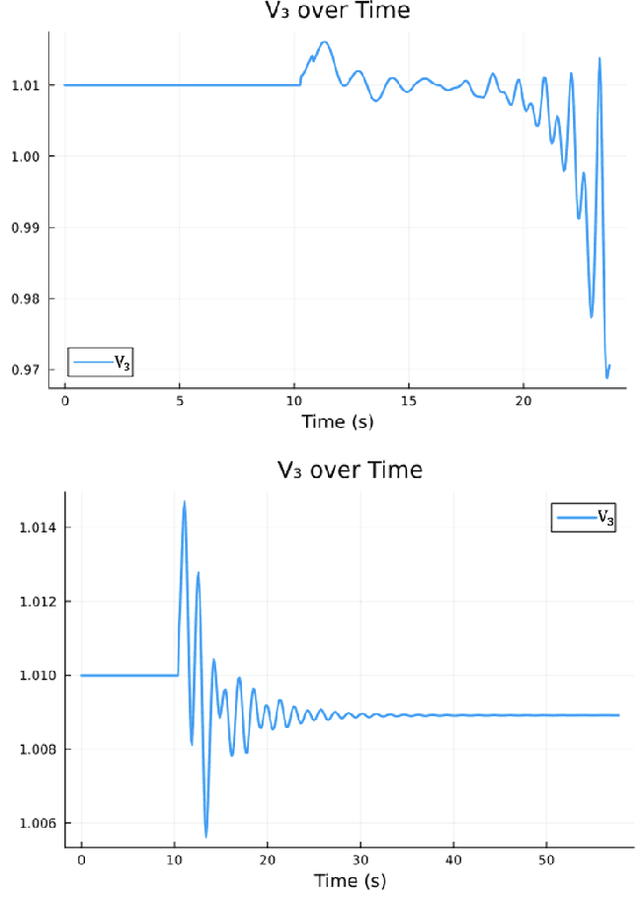
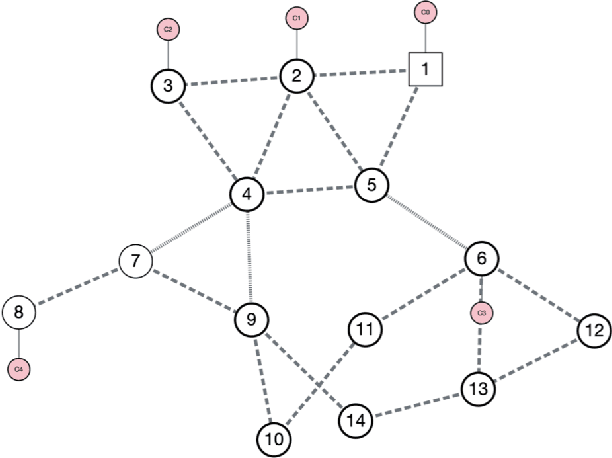
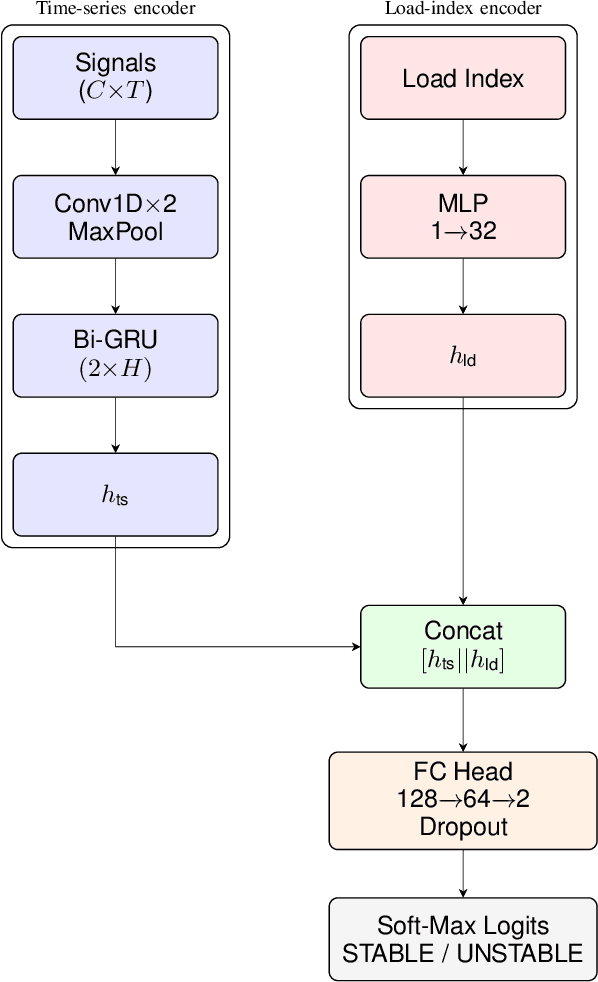
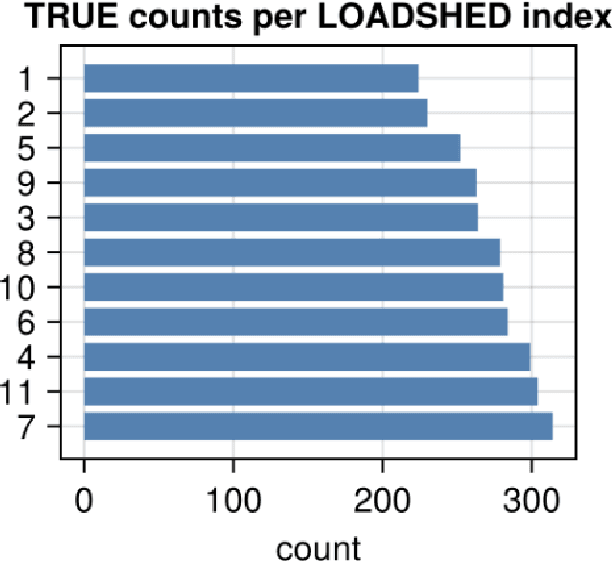
Every year critical infrastructure becomes more complex and we grow to rely on it more and more. With this reliance, it becomes an attractive target for cyberattacks from sophisticated actors, with one of the most attractive targets being the power grid. One class of attacks, instability attacks, is a newer type of attack that has relatively few protections developed. We present a cost effective, data-driven approach to training a supervised machine learning model to retrofit load shedding decision systems in power grids with the capacity to defend against instability attacks. We show a proof of concept on the IEEE 14 Bus System using the Achilles Heel Technologies Power Grid Analyzer, and show through an implementation of modified Prony analysis (MPA) that MPA is a viable method for detecting instability attacks and triggering defense mechanisms.

Trajectories for the Optimal Collection of Information

We study a scenario where an aircraft has multiple heterogeneous sensors collecting measurements to track a target vehicle of unknown location. The measurements are sampled along the flight path and our goals to optimize sensor placement to minimize estimation error. We select as a metric the Fisher Information Matrix (FIM), as "minimizing" the inverse of the FIM is required to achieve small estimation error. We propose to generate the optimal path from the Hamilton-Jacobi (HJ) partial differential equation (PDE) as it is the necessary and sufficient condition for optimality. A traditional method of lines (MOL) approach, based on a spatial grid, lends itself well to the highly non-linear and non-convex structure of the problem induced by the FIM matrix. However, the sensor placement problem results in a state space dimension that renders a naive MOL approach intractable. We present a new hybrid approach, whereby we decompose the state space into two parts: a smaller subspace that still uses a grid and takes advantage of the robustness to non-linearities and non-convexities, and the remaining state space that can by found efficiently from a system of ODEs, avoiding formation of a spatial grid.