Universally consistent vertex classification for latent positions graphs

In this work we show that, using the eigen-decomposition of the adjacency matrix, we can consistently estimate feature maps for latent position graphs with positive definite link function $\kappa$, provided that the latent positions are i.i.d. from some distribution F. We then consider the exploitation task of vertex classification where the link function $\kappa$ belongs to the class of universal kernels and class labels are observed for a number of vertices tending to infinity and that the remaining vertices are to be classified. We show that minimization of the empirical $\varphi$-risk for some convex surrogate $\varphi$ of 0-1 loss over a class of linear classifiers with increasing complexities yields a universally consistent classifier, that is, a classification rule with error converging to Bayes optimal for any distribution F.

Universally Consistent Latent Position Estimation and Vertex Classification for Random Dot Product Graphs

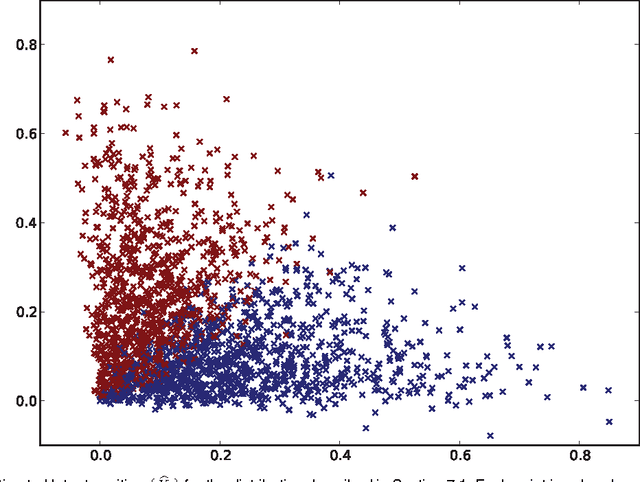
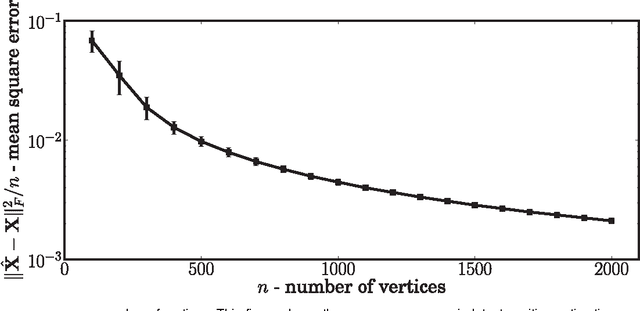
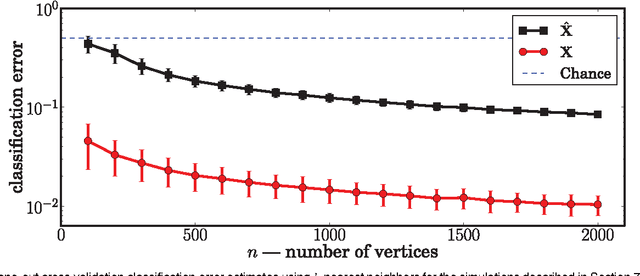
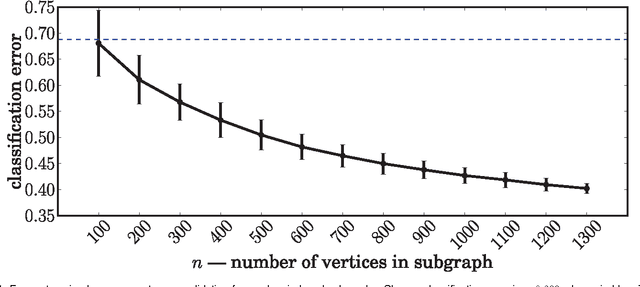
In this work we show that, using the eigen-decomposition of the adjacency matrix, we can consistently estimate latent positions for random dot product graphs provided the latent positions are i.i.d. from some distribution. If class labels are observed for a number of vertices tending to infinity, then we show that the remaining vertices can be classified with error converging to Bayes optimal using the $k$-nearest-neighbors classification rule. We evaluate the proposed methods on simulated data and a graph derived from Wikipedia.

A consistent adjacency spectral embedding for stochastic blockmodel graphs

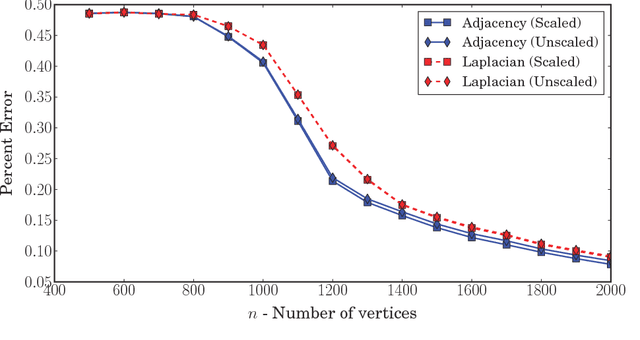
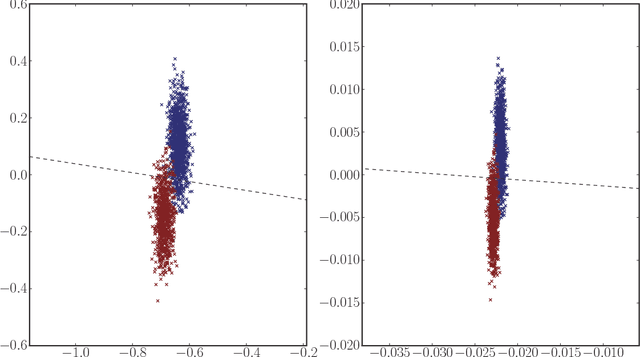
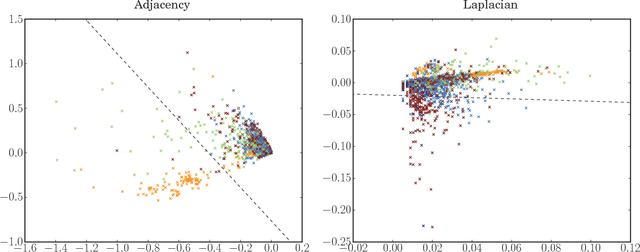
We present a method to estimate block membership of nodes in a random graph generated by a stochastic blockmodel. We use an embedding procedure motivated by the random dot product graph model, a particular example of the latent position model. The embedding associates each node with a vector; these vectors are clustered via minimization of a square error criterion. We prove that this method is consistent for assigning nodes to blocks, as only a negligible number of nodes will be mis-assigned. We prove consistency of the method for directed and undirected graphs. The consistent block assignment makes possible consistent parameter estimation for a stochastic blockmodel. We extend the result in the setting where the number of blocks grows slowly with the number of nodes. Our method is also computationally feasible even for very large graphs. We compare our method to Laplacian spectral clustering through analysis of simulated data and a graph derived from Wikipedia documents.