Zero- and Few-Shots Knowledge Graph Triplet Extraction with Large Language Models

In this work, we tested the Triplet Extraction (TE) capabilities of a variety of Large Language Models (LLMs) of different sizes in the Zero- and Few-Shots settings. In detail, we proposed a pipeline that dynamically gathers contextual information from a Knowledge Base (KB), both in the form of context triplets and of (sentence, triplets) pairs as examples, and provides it to the LLM through a prompt. The additional context allowed the LLMs to be competitive with all the older fully trained baselines based on the Bidirectional Long Short-Term Memory (BiLSTM) Network architecture. We further conducted a detailed analysis of the quality of the gathered KB context, finding it to be strongly correlated with the final TE performance of the model. In contrast, the size of the model appeared to only logarithmically improve the TE capabilities of the LLMs.

Product Jacobi-Theta Boltzmann machines with score matching

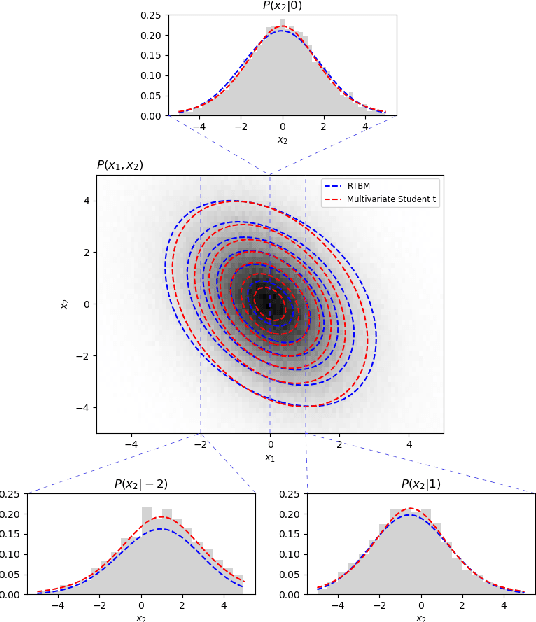
The estimation of probability density functions is a non trivial task that over the last years has been tackled with machine learning techniques. Successful applications can be obtained using models inspired by the Boltzmann machine (BM) architecture. In this manuscript, the product Jacobi-Theta Boltzmann machine (pJTBM) is introduced as a restricted version of the Riemann-Theta Boltzmann machine (RTBM) with diagonal hidden sector connection matrix. We show that score matching, based on the Fisher divergence, can be used to fit probability densities with the pJTBM more efficiently than with the original RTBM.

Modelling conditional probabilities with Riemann-Theta Boltzmann Machines

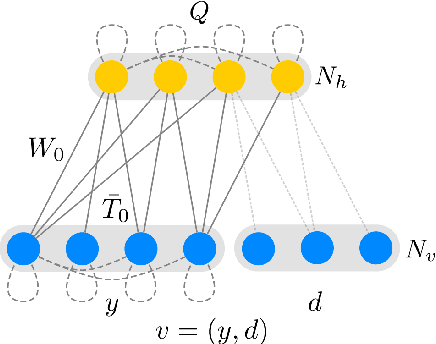
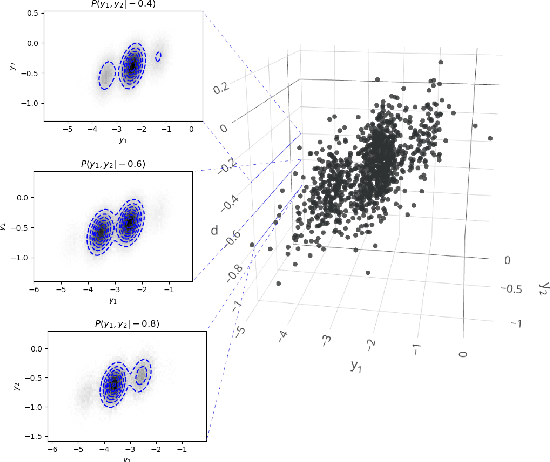
The probability density function for the visible sector of a Riemann-Theta Boltzmann machine can be taken conditional on a subset of the visible units. We derive that the corresponding conditional density function is given by a reparameterization of the Riemann-Theta Boltzmann machine modelling the original probability density function. Therefore the conditional densities can be directly inferred from the Riemann-Theta Boltzmann machine.

Sampling the Riemann-Theta Boltzmann Machine

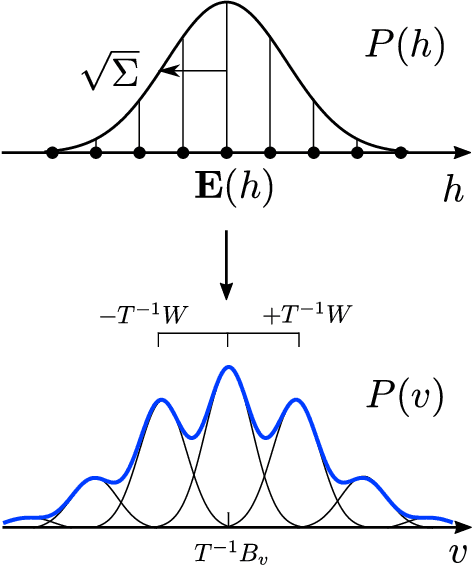
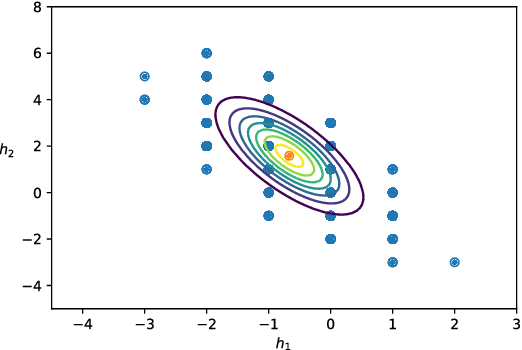
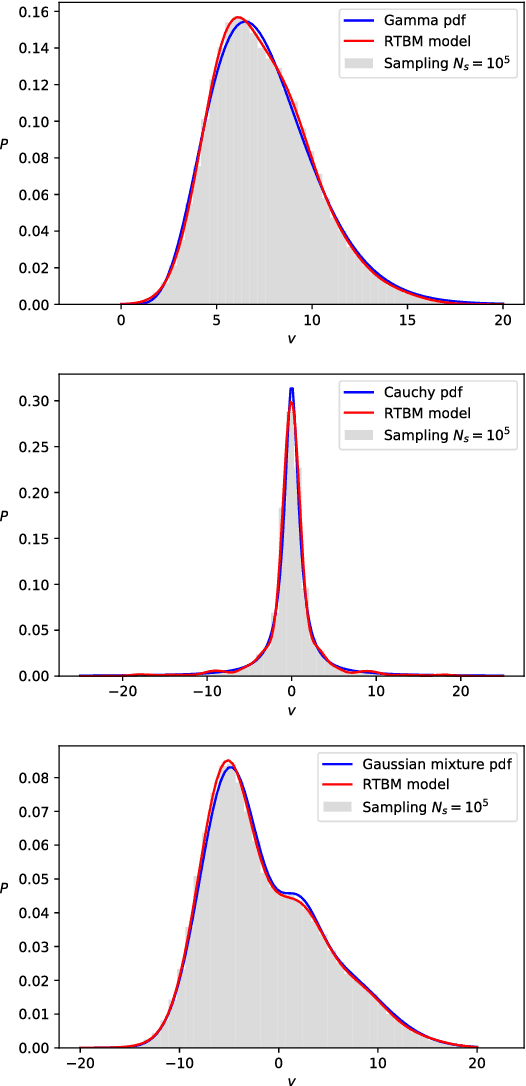
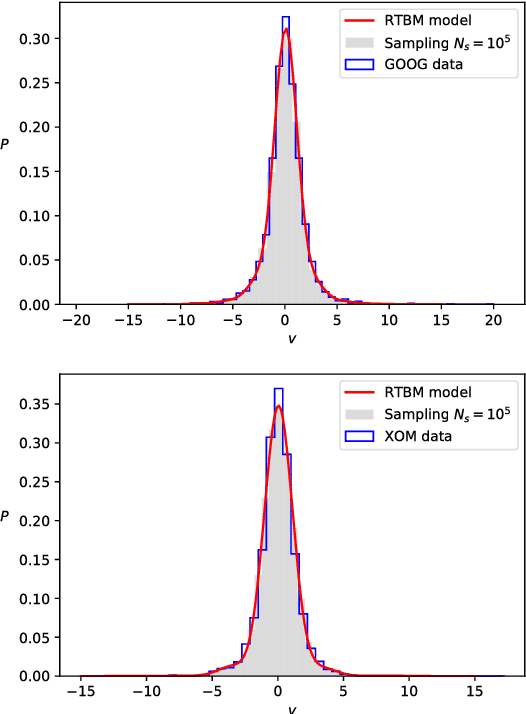
We show that the visible sector probability density function of the Riemann-Theta Boltzmann machine corresponds to a gaussian mixture model consisting of an infinite number of component multi-variate gaussians. The weights of the mixture are given by a discrete multi-variate gaussian over the hidden state space. This allows us to sample the visible sector density function in a straight-forward manner. Furthermore, we show that the visible sector probability density function possesses an affine transform property, similar to the multi-variate gaussian density.

Riemann-Theta Boltzmann Machine

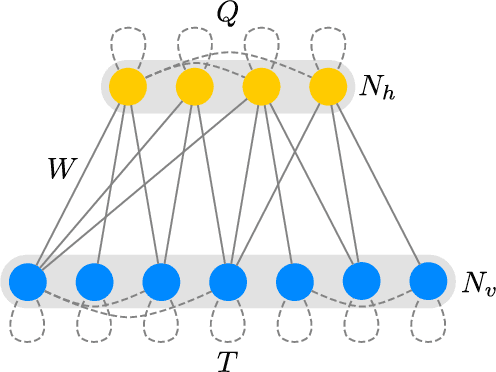
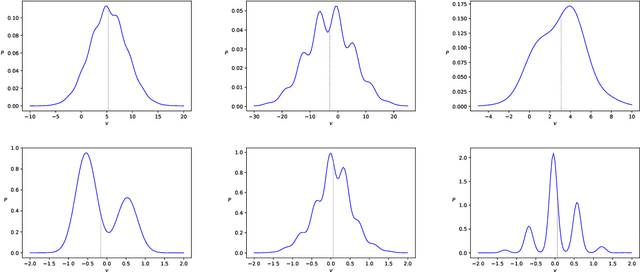
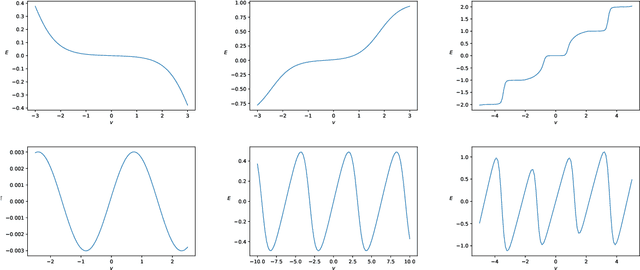
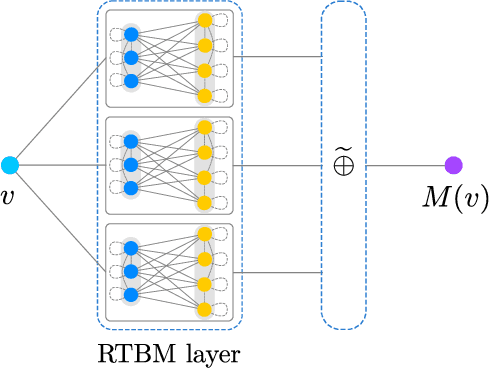
A general Boltzmann machine with continuous visible and discrete integer valued hidden states is introduced. Under mild assumptions about the connection matrices, the probability density function of the visible units can be solved for analytically, yielding a novel parametric density function involving a ratio of Riemann-Theta functions. The conditional expectation of a hidden state for given visible states can also be calculated analytically, yielding a derivative of the logarithmic Riemann-Theta function. The conditional expectation can be used as activation function in a feedforward neural network, thereby increasing the modelling capacity of the network. Both the Boltzmann machine and the derived feedforward neural network can be successfully trained via standard gradient- and non-gradient-based optimization techniques.