On instabilities in neural network-based physics simulators

When neural networks are trained from data to simulate the dynamics of physical systems, they encounter a persistent challenge: the long-time dynamics they produce are often unphysical or unstable. We analyze the origin of such instabilities when learning linear dynamical systems, focusing on the training dynamics. We make several analytical findings which empirical observations suggest extend to nonlinear dynamical systems. First, the rate of convergence of the training dynamics is uneven and depends on the distribution of energy in the data. As a special case, the dynamics in directions where the data have no energy cannot be learned. Second, in the unlearnable directions, the dynamics produced by the neural network depend on the weight initialization, and common weight initialization schemes can produce unstable dynamics. Third, injecting synthetic noise into the data during training adds damping to the training dynamics and can stabilize the learned simulator, though doing so undesirably biases the learned dynamics. For each contributor to instability, we suggest mitigative strategies. We also highlight important differences between learning discrete-time and continuous-time dynamics, and discuss extensions to nonlinear systems.

Charts and atlases for nonlinear data-driven models of dynamics on manifolds

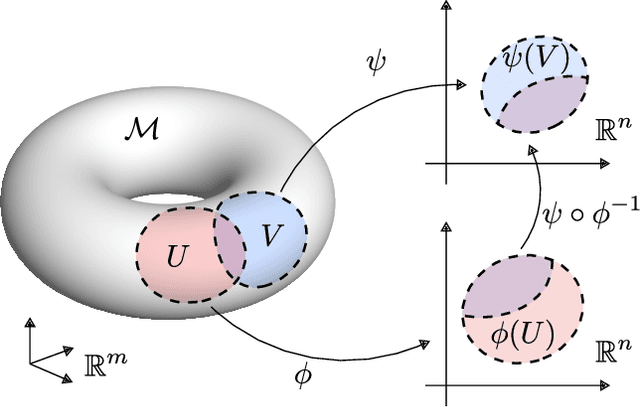
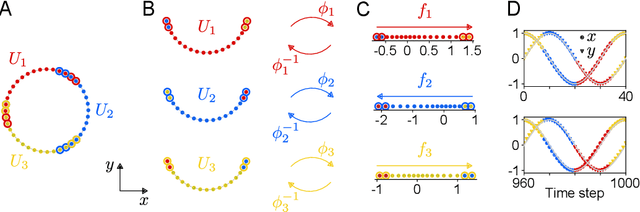
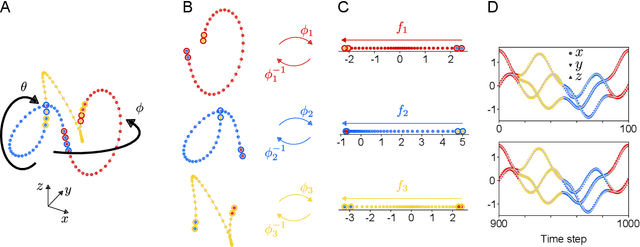
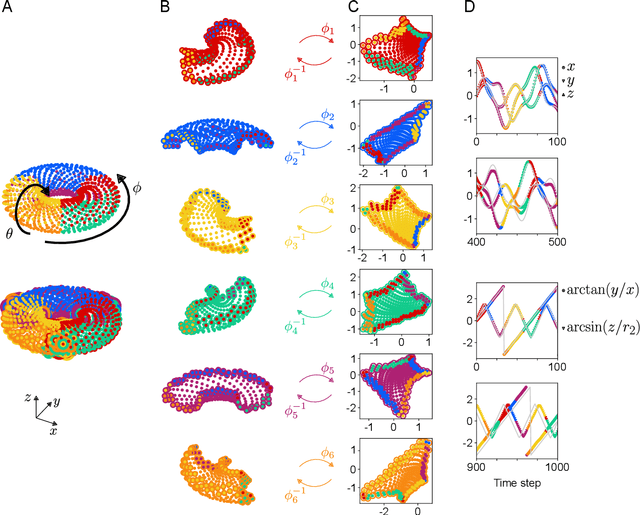
We introduce a method for learning minimal-dimensional dynamical models from high-dimensional time series data that lie on a low-dimensional manifold, as arises for many processes. For an arbitrary manifold, there is no smooth global coordinate representation, so following the formalism of differential topology we represent the manifold as an atlas of charts. We first partition the data into overlapping regions. Then undercomplete autoencoders are used to find low-dimensional coordinate representations for each region. We then use the data to learn dynamical models in each region, which together yield a global low-dimensional dynamical model. We apply this method to examples ranging from simple periodic dynamics to complex, nominally high-dimensional non-periodic bursting dynamics of the Kuramoto-Sivashinsky equation. We demonstrate that it: (1) can yield dynamical models of the lowest possible dimension, where previous methods generally cannot; (2) exhibits computational benefits including scalability, parallelizability, and adaptivity; and (3) separates state space into regions of distinct behaviours.