Distribution Matching for Graph Quantification Under Structural Covariate Shift

Graphs are commonly used in machine learning to model relationships between instances. Consider the task of predicting the political preferences of users in a social network; to solve this task one should consider, both, the features of each individual user and the relationships between them. However, oftentimes one is not interested in the label of a single instance but rather in the distribution of labels over a set of instances; e.g., when predicting the political preferences of users, the overall prevalence of a given opinion might be of higher interest than the opinion of a specific person. This label prevalence estimation task is commonly referred to as quantification learning (QL). Current QL methods for tabular data are typically based on the so-called prior probability shift (PPS) assumption which states that the label-conditional instance distributions should remain equal across the training and test data. In the graph setting, PPS generally does not hold if the shift between training and test data is structural, i.e., if the training data comes from a different region of the graph than the test data. To address such structural shifts, an importance sampling variant of the popular adjusted count quantification approach has previously been proposed. In this work, we extend the idea of structural importance sampling to the state-of-the-art KDEy quantification approach. We show that our proposed method adapts to structural shifts and outperforms standard quantification approaches.

Adjusted Count Quantification Learning on Graphs

Quantification learning is the task of predicting the label distribution of a set of instances. We study this problem in the context of graph-structured data, where the instances are vertices. Previously, this problem has only been addressed via node clustering methods. In this paper, we extend the popular Adjusted Classify & Count (ACC) method to graphs. We show that the prior probability shift assumption upon which ACC relies is often not fulfilled and propose two novel graph quantification techniques: Structural importance sampling (SIS) makes ACC applicable in graph domains with covariate shift. Neighborhood-aware ACC improves quantification in the presence of non-homophilic edges. We show the effectiveness of our techniques on multiple graph quantification tasks.

CUQ-GNN: Committee-based Graph Uncertainty Quantification using Posterior Networks

In this work, we study the influence of domain-specific characteristics when defining a meaningful notion of predictive uncertainty on graph data. Previously, the so-called Graph Posterior Network (GPN) model has been proposed to quantify uncertainty in node classification tasks. Given a graph, it uses Normalizing Flows (NFs) to estimate class densities for each node independently and converts those densities into Dirichlet pseudo-counts, which are then dispersed through the graph using the personalized Page-Rank algorithm. The architecture of GPNs is motivated by a set of three axioms on the properties of its uncertainty estimates. We show that those axioms are not always satisfied in practice and therefore propose the family of Committe-based Uncertainty Quantification Graph Neural Networks (CUQ-GNNs), which combine standard Graph Neural Networks with the NF-based uncertainty estimation of Posterior Networks (PostNets). This approach adapts more flexibly to domain-specific demands on the properties of uncertainty estimates. We compare CUQ-GNN against GPN and other uncertainty quantification approaches on common node classification benchmarks and show that it is effective at producing useful uncertainty estimates.

Linear Opinion Pooling for Uncertainty Quantification on Graphs

We address the problem of uncertainty quantification for graph-structured data, or, more specifically, the problem to quantify the predictive uncertainty in (semi-supervised) node classification. Key questions in this regard concern the distinction between two different types of uncertainty, aleatoric and epistemic, and how to support uncertainty quantification by leveraging the structural information provided by the graph topology. Challenging assumptions and postulates of state-of-the-art methods, we propose a novel approach that represents (epistemic) uncertainty in terms of mixtures of Dirichlet distributions and refers to the established principle of linear opinion pooling for propagating information between neighbored nodes in the graph. The effectiveness of this approach is demonstrated in a series of experiments on a variety of graph-structured datasets.

Ranking Structured Objects with Graph Neural Networks

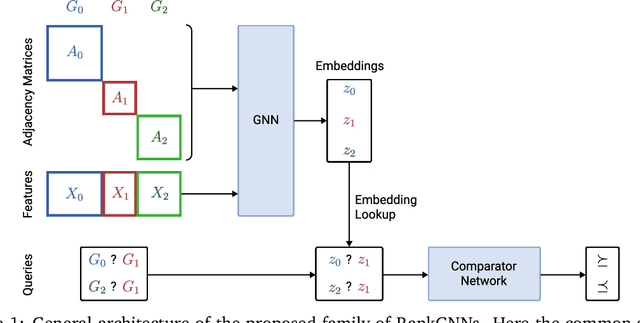
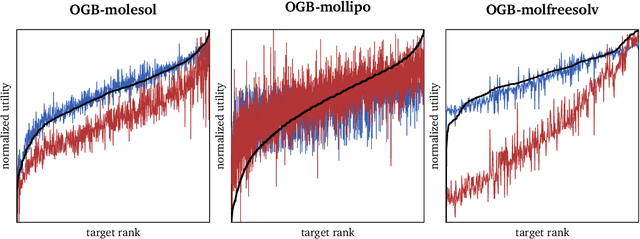
Graph neural networks (GNNs) have been successfully applied in many structured data domains, with applications ranging from molecular property prediction to the analysis of social networks. Motivated by the broad applicability of GNNs, we propose the family of so-called RankGNNs, a combination of neural Learning to Rank (LtR) methods and GNNs. RankGNNs are trained with a set of pair-wise preferences between graphs, suggesting that one of them is preferred over the other. One practical application of this problem is drug screening, where an expert wants to find the most promising molecules in a large collection of drug candidates. We empirically demonstrate that our proposed pair-wise RankGNN approach either significantly outperforms or at least matches the ranking performance of the naive point-wise baseline approach, in which the LtR problem is solved via GNN-based graph regression.

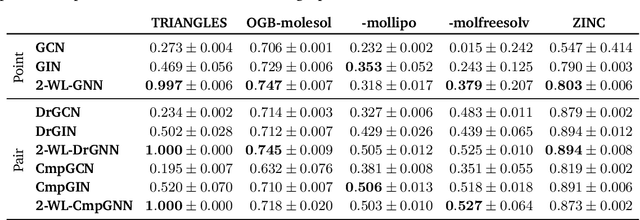
A Novel Higher-order Weisfeiler-Lehman Graph Convolution

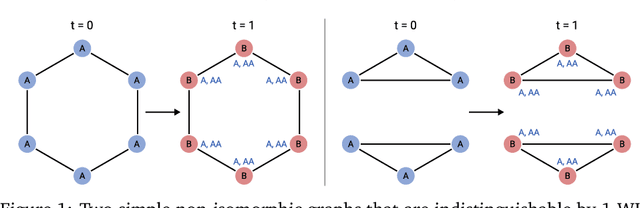
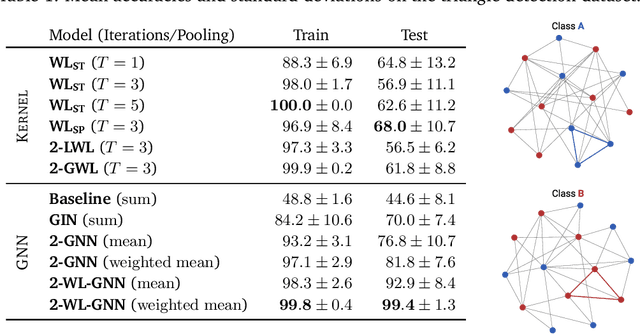
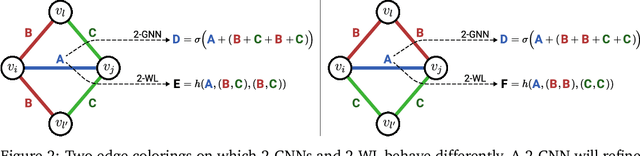
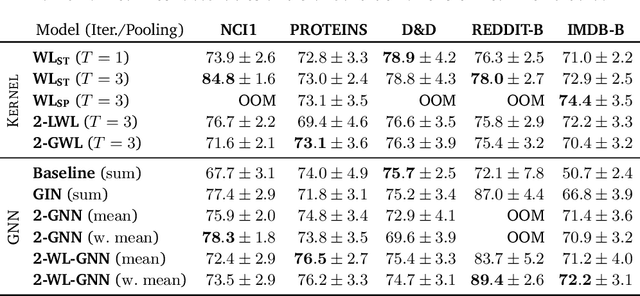
Current GNN architectures use a vertex neighborhood aggregation scheme, which limits their discriminative power to that of the 1-dimensional Weisfeiler-Lehman (WL) graph isomorphism test. Here, we propose a novel graph convolution operator that is based on the 2-dimensional WL test. We formally show that the resulting 2-WL-GNN architecture is more discriminative than existing GNN approaches. This theoretical result is complemented by experimental studies using synthetic and real data. On multiple common graph classification benchmarks, we demonstrate that the proposed model is competitive with state-of-the-art graph kernels and GNNs.