Sample Size Planning for Classification Models

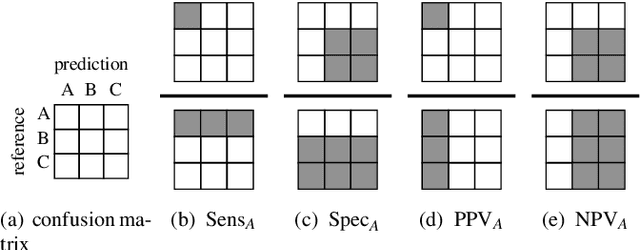
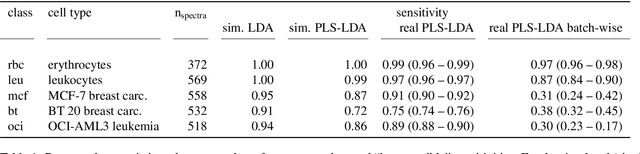
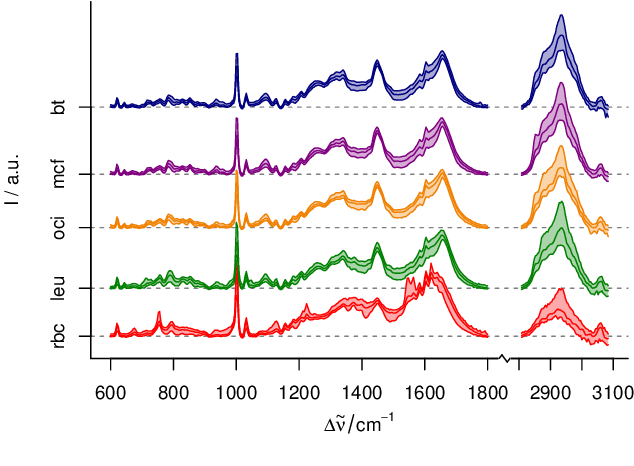
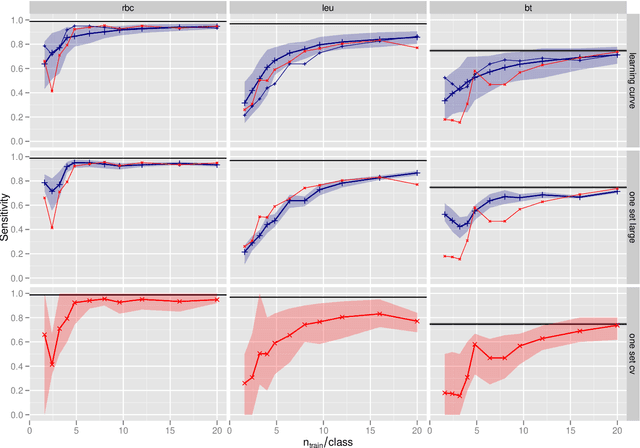
In biospectroscopy, suitably annotated and statistically independent samples (e. g. patients, batches, etc.) for classifier training and testing are scarce and costly. Learning curves show the model performance as function of the training sample size and can help to determine the sample size needed to train good classifiers. However, building a good model is actually not enough: the performance must also be proven. We discuss learning curves for typical small sample size situations with 5 - 25 independent samples per class. Although the classification models achieve acceptable performance, the learning curve can be completely masked by the random testing uncertainty due to the equally limited test sample size. In consequence, we determine test sample sizes necessary to achieve reasonable precision in the validation and find that 75 - 100 samples will usually be needed to test a good but not perfect classifier. Such a data set will then allow refined sample size planning on the basis of the achieved performance. We also demonstrate how to calculate necessary sample sizes in order to show the superiority of one classifier over another: this often requires hundreds of statistically independent test samples or is even theoretically impossible. We demonstrate our findings with a data set of ca. 2550 Raman spectra of single cells (five classes: erythrocytes, leukocytes and three tumour cell lines BT-20, MCF-7 and OCI-AML3) as well as by an extensive simulation that allows precise determination of the actual performance of the models in question.

Validation of Soft Classification Models using Partial Class Memberships: An Extended Concept of Sensitivity & Co. applied to the Grading of Astrocytoma Tissues

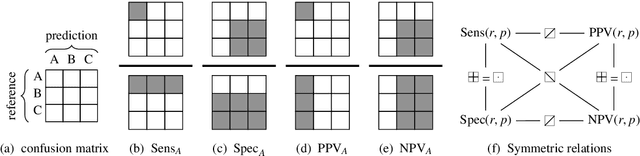
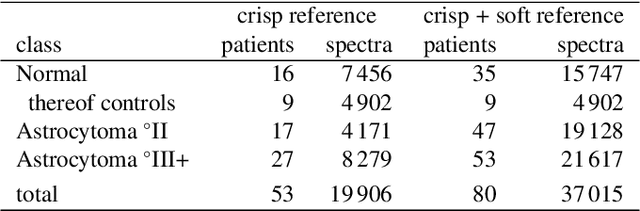
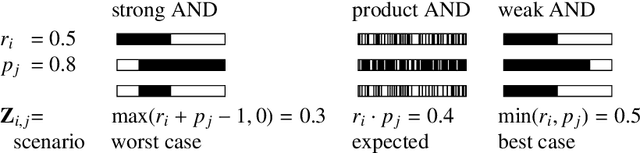
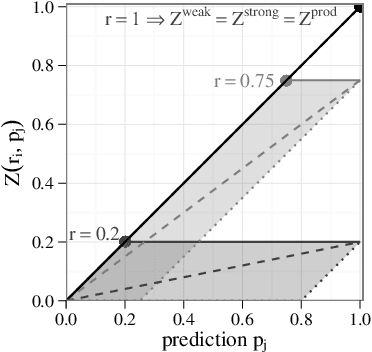
We use partial class memberships in soft classification to model uncertain labelling and mixtures of classes. Partial class memberships are not restricted to predictions, but may also occur in reference labels (ground truth, gold standard diagnosis) for training and validation data. Classifier performance is usually expressed as fractions of the confusion matrix, such as sensitivity, specificity, negative and positive predictive values. We extend this concept to soft classification and discuss the bias and variance properties of the extended performance measures. Ambiguity in reference labels translates to differences between best-case, expected and worst-case performance. We show a second set of measures comparing expected and ideal performance which is closely related to regression performance, namely the root mean squared error RMSE and the mean absolute error MAE. All calculations apply to classical crisp classification as well as to soft classification (partial class memberships and/or one-class classifiers). The proposed performance measures allow to test classifiers with actual borderline cases. In addition, hardening of e.g. posterior probabilities into class labels is not necessary, avoiding the corresponding information loss and increase in variance. We implement the proposed performance measures in the R package "softclassval", which is available from CRAN and at http://softclassval.r-forge.r-project.org. Our reasoning as well as the importance of partial memberships for chemometric classification is illustrated by a real-word application: astrocytoma brain tumor tissue grading (80 patients, 37000 spectra) for finding surgical excision borders. As borderline cases are the actual target of the analytical technique, samples which are diagnosed to be borderline cases must be included in the validation.