Christopher Syben
Pattern Recognition Lab, Department of Computer Science, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany
Learning with Known Operators reduces Maximum Training Error Bounds
Jul 03, 2019
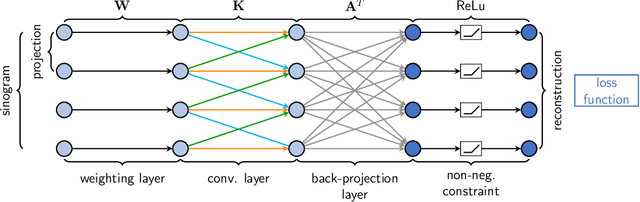
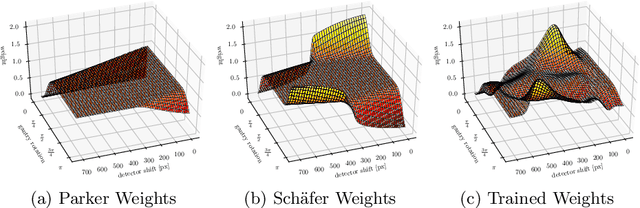
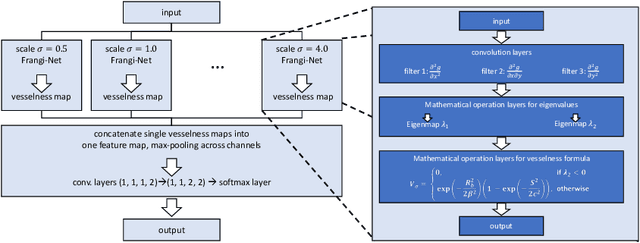
Abstract:We describe an approach for incorporating prior knowledge into machine learning algorithms. We aim at applications in physics and signal processing in which we know that certain operations must be embedded into the algorithm. Any operation that allows computation of a gradient or sub-gradient towards its inputs is suited for our framework. We derive a maximal error bound for deep nets that demonstrates that inclusion of prior knowledge results in its reduction. Furthermore, we also show experimentally that known operators reduce the number of free parameters. We apply this approach to various tasks ranging from CT image reconstruction over vessel segmentation to the derivation of previously unknown imaging algorithms. As such the concept is widely applicable for many researchers in physics, imaging, and signal processing. We assume that our analysis will support further investigation of known operators in other fields of physics, imaging, and signal processing.
PYRO-NN: Python Reconstruction Operators in Neural Networks
Apr 30, 2019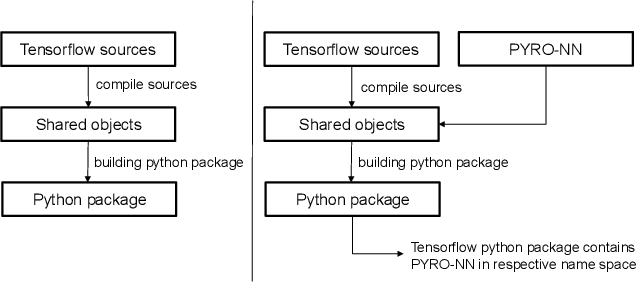
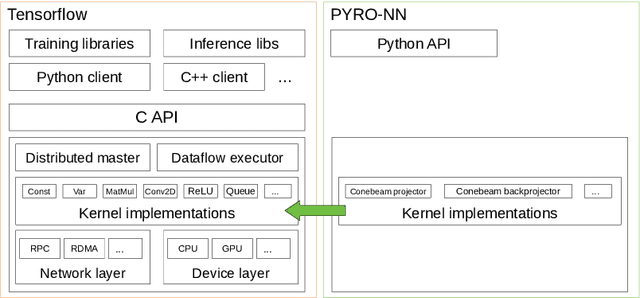
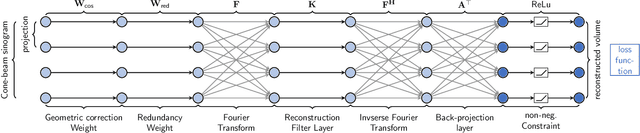
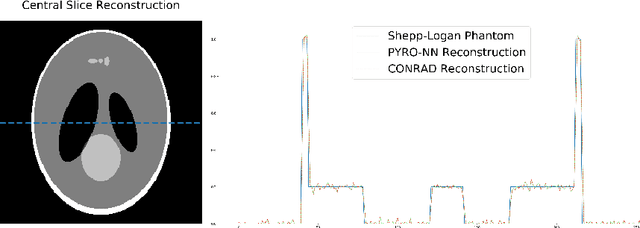
Abstract:Purpose: Recently, several attempts were conducted to transfer deep learning to medical image reconstruction. An increasingly number of publications follow the concept of embedding the CT reconstruction as a known operator into a neural network. However, most of the approaches presented lack an efficient CT reconstruction framework fully integrated into deep learning environments. As a result, many approaches are forced to use workarounds for mathematically unambiguously solvable problems. Methods: PYRO-NN is a generalized framework to embed known operators into the prevalent deep learning framework Tensorflow. The current status includes state-of-the-art parallel-, fan- and cone-beam projectors and back-projectors accelerated with CUDA provided as Tensorflow layers. On top, the framework provides a high level Python API to conduct FBP and iterative reconstruction experiments with data from real CT systems. Results: The framework provides all necessary algorithms and tools to design end-to-end neural network pipelines with integrated CT reconstruction algorithms. The high level Python API allows a simple use of the layers as known from Tensorflow. To demonstrate the capabilities of the layers, the framework comes with three baseline experiments showing a cone-beam short scan FDK reconstruction, a CT reconstruction filter learning setup, and a TV regularized iterative reconstruction. All algorithms and tools are referenced to a scientific publication and are compared to existing non deep learning reconstruction frameworks. The framework is available as open-source software at \url{https://github.com/csyben/PYRO-NN}. Conclusions: PYRO-NN comes with the prevalent deep learning framework Tensorflow and allows to setup end-to-end trainable neural networks in the medical image reconstruction context. We believe that the framework will be a step towards reproducible research
Deriving Neural Network Architectures using Precision Learning: Parallel-to-fan beam Conversion
Oct 23, 2018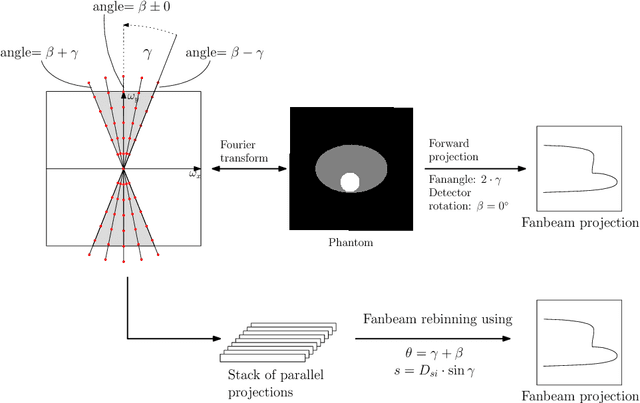
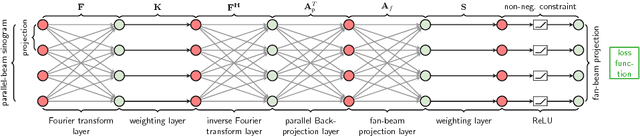

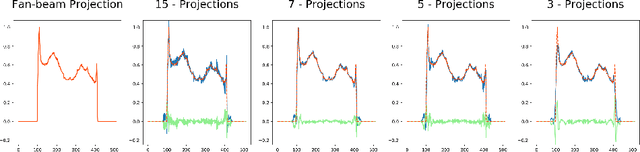
Abstract:In this paper, we derive a neural network architecture based on an analytical formulation of the parallel-to-fan beam conversion problem following the concept of precision learning. The network allows to learn the unknown operators in this conversion in a data-driven manner avoiding interpolation and potential loss of resolution. Integration of known operators results in a small number of trainable parameters that can be estimated from synthetic data only. The concept is evaluated in the context of Hybrid MRI/X-ray imaging where transformation of the parallel-beam MRI projections to fan-beam X-ray projections is required. The proposed method is compared to a traditional rebinning method. The results demonstrate that the proposed method is superior to ray-by-ray interpolation and is able to deliver sharper images using the same amount of parallel-beam input projections which is crucial for interventional applications. We believe that this approach forms a basis for further work uniting deep learning, signal processing, physics, and traditional pattern recognition.
A Gentle Introduction to Deep Learning in Medical Image Processing
Oct 12, 2018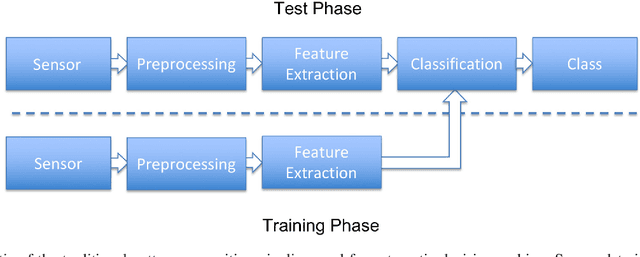
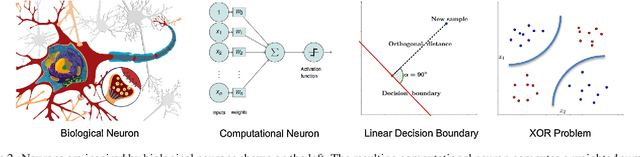
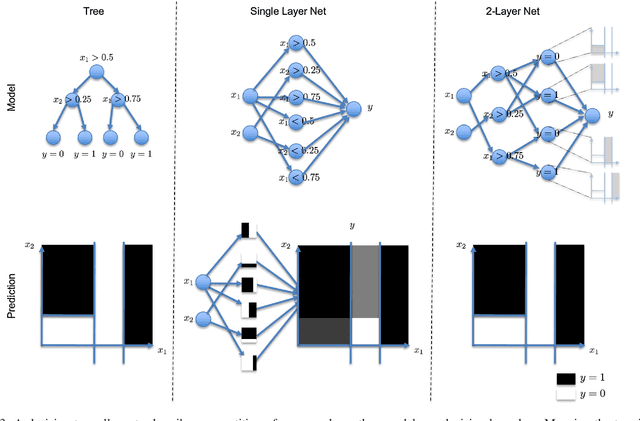
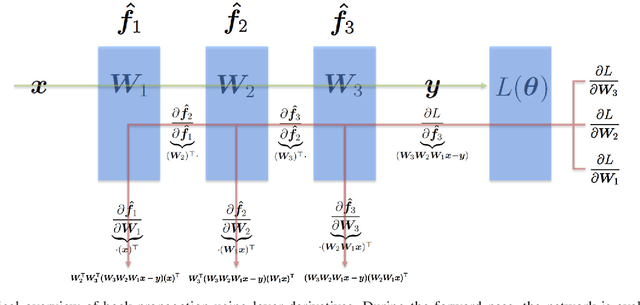
Abstract:This paper tries to give a gentle introduction to deep learning in medical image processing, proceeding from theoretical foundations to applications. We first discuss general reasons for the popularity of deep learning, including several major breakthroughs in computer science. Next, we start reviewing the fundamental basics of the perceptron and neural networks, along with some fundamental theory that is often omitted. Doing so allows us to understand the reasons for the rise of deep learning in many application domains. Obviously medical image processing is one of these areas which has been largely affected by this rapid progress, in particular in image detection and recognition, image segmentation, image registration, and computer-aided diagnosis. There are also recent trends in physical simulation, modelling, and reconstruction that have led to astonishing results. Yet, some of these approaches neglect prior knowledge and hence bear the risk of producing implausible results. These apparent weaknesses highlight current limitations of deep learning. However, we also briefly discuss promising approaches that might be able to resolve these problems in the future.
Precision Learning: Towards Use of Known Operators in Neural Networks
Oct 12, 2018
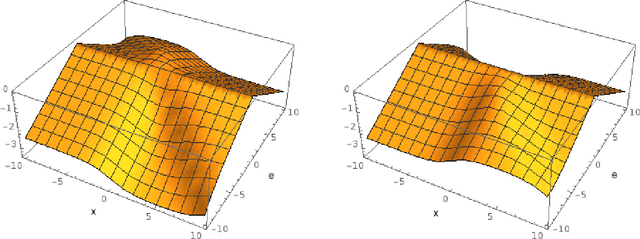
Abstract:In this paper, we consider the use of prior knowledge within neural networks. In particular, we investigate the effect of a known transform within the mapping from input data space to the output domain. We demonstrate that use of known transforms is able to change maximal error bounds. In order to explore the effect further, we consider the problem of X-ray material decomposition as an example to incorporate additional prior knowledge. We demonstrate that inclusion of a non-linear function known from the physical properties of the system is able to reduce prediction errors therewith improving prediction quality from SSIM values of 0.54 to 0.88. This approach is applicable to a wide set of applications in physics and signal processing that provide prior knowledge on such transforms. Also maximal error estimation and network understanding could be facilitated within the context of precision learning.
* accepted on ICPR 2018
User Loss -- A Forced-Choice-Inspired Approach to Train Neural Networks directly by User Interaction
Jul 24, 2018
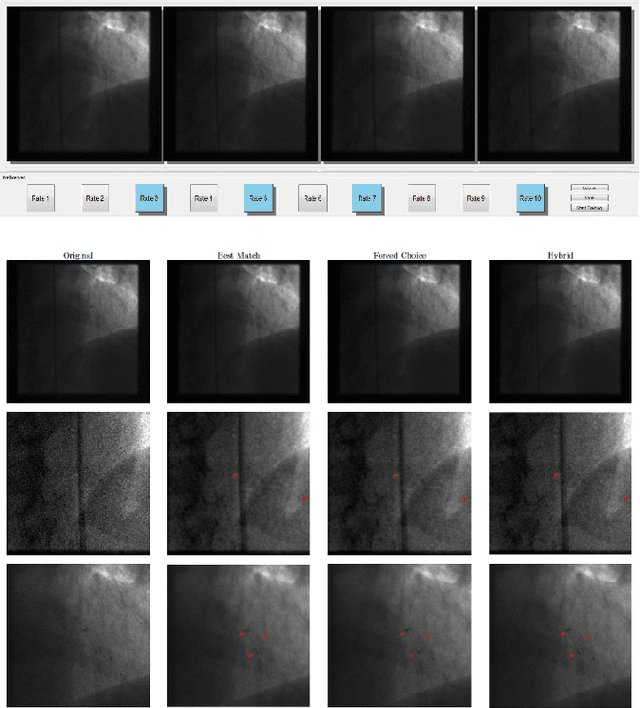
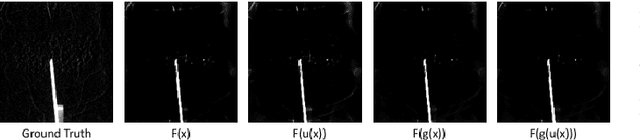
Abstract:In this paper, we investigate whether is it possible to train a neural network directly from user inputs. We consider this approach to be highly relevant for applications in which the point of optimality is not well-defined and user-dependent. Our application is medical image denoising which is essential in fluoroscopy imaging. In this field every user, i.e. physician, has a different flavor and image quality needs to be tailored towards each individual. To address this important problem, we propose to construct a loss function derived from a forced-choice experiment. In order to make the learning problem feasible, we operate in the domain of precision learning, i.e., we inspire the network architecture by traditional signal processing methods in order to reduce the number of trainable parameters. The algorithm that was used for this is a Laplacian pyramid with only six trainable parameters. In the experimental results, we demonstrate that two image experts who prefer different filter characteristics between sharpness and de-noising can be created using our approach. Also models trained for a specific user perform best on this users test data. This approach opens the way towards implementation of direct user feedback in deep learning and is applicable for a wide range of application.
Precision Learning: Reconstruction Filter Kernel Discretization
Jul 09, 2018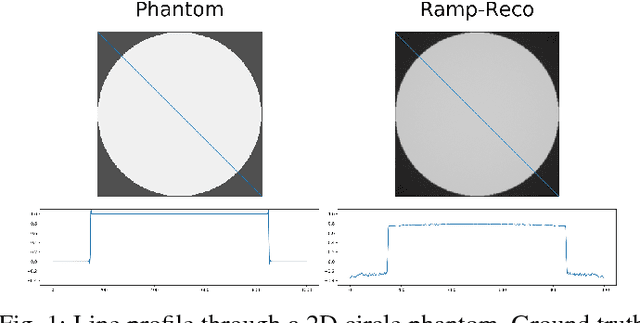
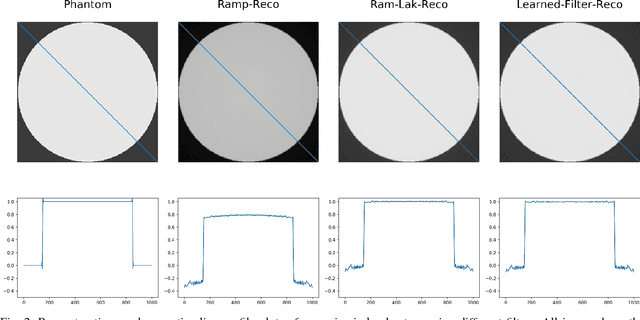
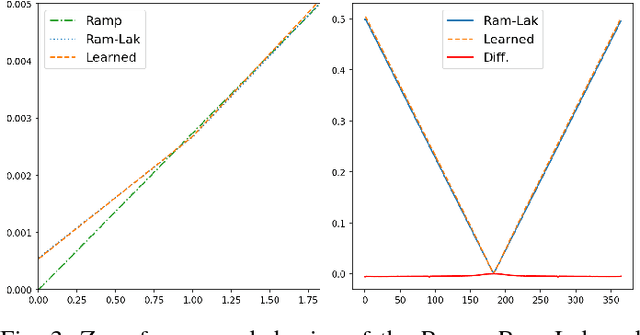
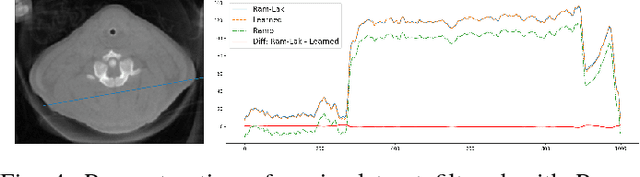
Abstract:In this paper, we present substantial evidence that a deep neural network will intrinsically learn the appropriate way to discretize the ideal continuous reconstruction filter. Currently, the Ram-Lak filter or heuristic filters which impose different noise assumptions are used for filtered back-projection. All of these, however, inhibit a fully data-driven reconstruction deep learning approach. In addition, the heuristic filters are not chosen in an optimal sense. To tackle this issue, we propose a formulation to directly learn the reconstruction filter. The filter is initialized with the ideal Ramp filter as a strong pre-training and learned in frequency domain. We compare the learned filter with the Ram-Lak and the Ramp filter on a numerical phantom as well as on a real CT dataset. The results show that the network properly discretizes the continuous Ramp filter and converges towards the Ram-Lak solution. In our view these observations are interesting to gain a better understanding of deep learning techniques and traditional analytic techniques such as Wiener filtering and discretization theory. Furthermore, this will allow fully trainable data-driven reconstruction deep learning approaches.
Projection image-to-image translation in hybrid X-ray/MR imaging
Apr 11, 2018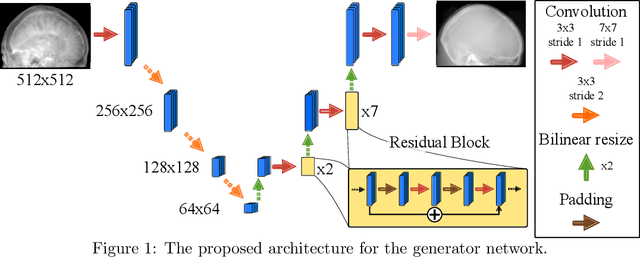
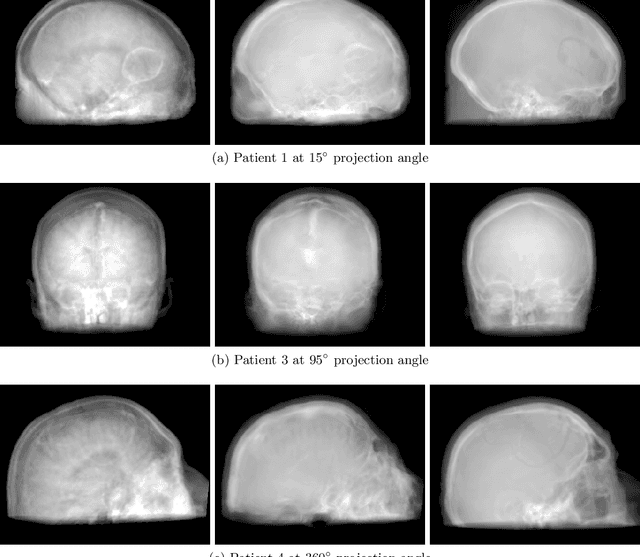
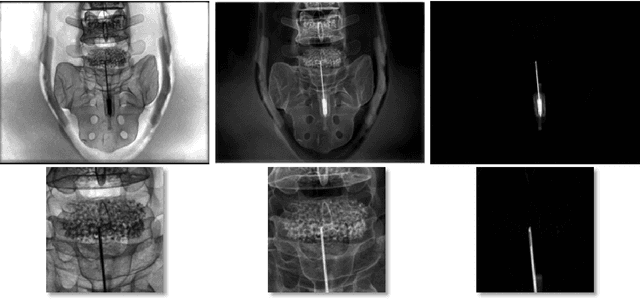
Abstract:The potential benefit of hybrid X-ray and MR imaging in the interventional environment is enormous. However, a vast amount of existing image enhancement methods requires the image information to be present in the same domain. To unlock this potential, we present a solution to image-to-image translation from MR projections to corresponding X-ray projection images. The approach is based on a state-of-the-art image generator network that is modified to fit the specific application. Furthermore, we propose the inclusion of a gradient map to the perceptual loss to emphasize high frequency details. The proposed approach is capable of creating X-ray projection images with natural appearance. Additionally, our extensions show clear improvement compared to the baseline method.
MR to X-Ray Projection Image Synthesis
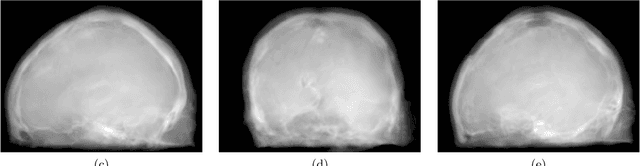
Apr 03, 2018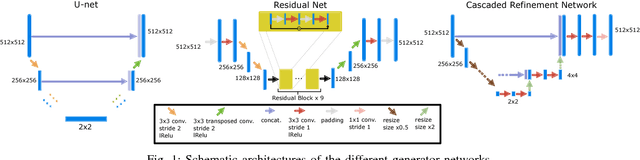
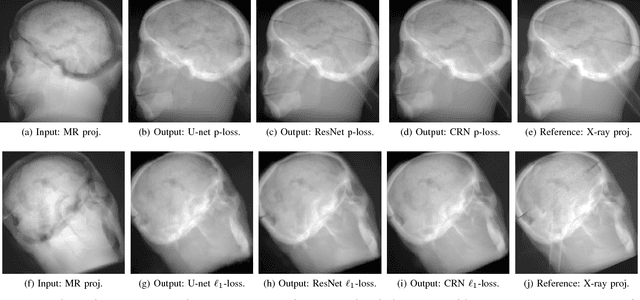
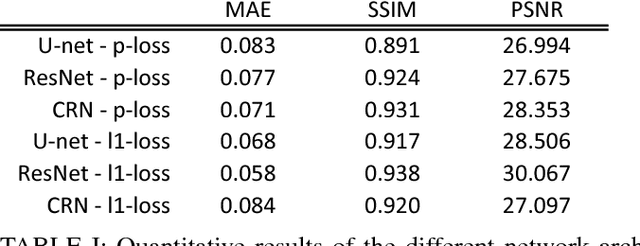
Abstract:Hybrid imaging promises large potential in medical imaging applications. To fully utilize the possibilities of corresponding information from different modalities, the information must be transferable between the domains. In radiation therapy planning, existing methods make use of reconstructed 3D magnetic resonance imaging data to synthesize corresponding X-ray attenuation maps. In contrast, for fluoroscopic procedures only line integral data, i.e., 2D projection images, are present. The question arises which approaches could potentially be used for this MR to X-ray projection image-to-image translation. We examine three network architectures and two loss-functions regarding their suitability as generator networks for this task. All generators proved to yield suitable results for this task. A cascaded refinement network paired with a perceptual-loss function achieved the best qualitative results in our evaluation. The perceptual-loss showed to be able to preserve most of the high-frequency details in the projection images and, thus, is recommended for the underlying task and similar problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge