Christoph Schultheiss
Assessing the overall and partial causal well-specification of nonlinear additive noise models
Oct 26, 2023



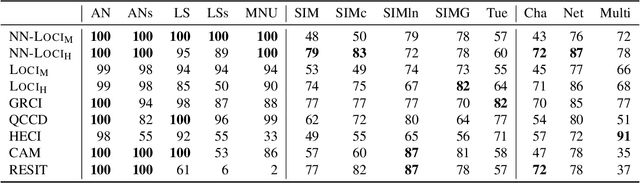
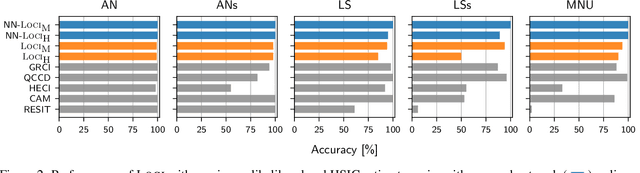
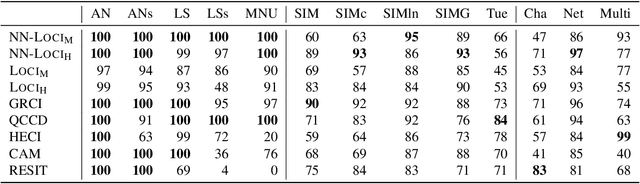
Abstract:We propose a method to detect model misspecifications in nonlinear causal additive and potentially heteroscedastic noise models. We aim to identify predictor variables for which we can infer the causal effect even in cases of such misspecification. We develop a general framework based on knowledge of the multivariate observational data distribution and we then propose an algorithm for finite sample data, discuss its asymptotic properties, and illustrate its performance on simulated and real data.
On the Identifiability and Estimation of Causal Location-Scale Noise Models
Oct 13, 2022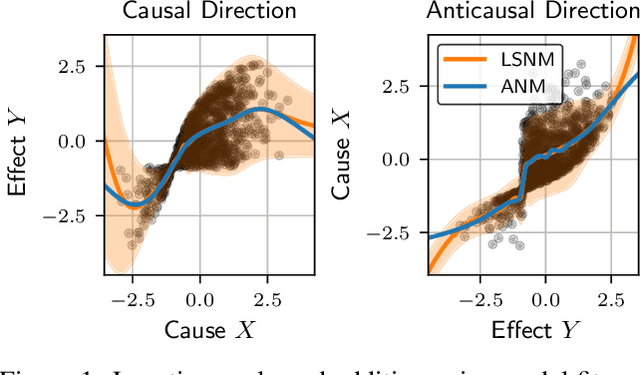
Abstract:We study the class of location-scale or heteroscedastic noise models (LSNMs), in which the effect $Y$ can be written as a function of the cause $X$ and a noise source $N$ independent of $X$, which may be scaled by a positive function $g$ over the cause, i.e., $Y = f(X) + g(X)N$. Despite the generality of the model class, we show the causal direction is identifiable up to some pathological cases. To empirically validate these theoretical findings, we propose two estimators for LSNMs: an estimator based on (non-linear) feature maps, and one based on probabilistic neural networks. Both model the conditional distribution of $Y$ given $X$ as a Gaussian parameterized by its natural parameters. Since the neural network approach can fit functions of arbitrary complexity, it has an edge over the feature map-based approach in terms of empirical performance. When the feature maps are correctly specified, however, we can prove that our estimator is jointly concave, which allows us to derive stronger guarantees for the cause-effect identification task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge