RPCA-KFE: Key Frame Extraction for Consumer Video based Robust Principal Component Analysis

Key frame extraction algorithms consider the problem of selecting a subset of the most informative frames from a video to summarize its content.

Representative Selection for Big Data via Sparse Graph and Geodesic Grassmann Manifold Distance

This paper addresses the problem of identifying a very small subset of data points that belong to a significantly larger massive dataset (i.e., Big Data). The small number of selected data points must adequately represent and faithfully characterize the massive Big Data. Such identification process is known as representative selection [19]. We propose a novel representative selection framework by generating an l1 norm sparse graph for a given Big-Data dataset. The Big Data is partitioned recursively into clusters using a spectral clustering algorithm on the generated sparse graph. We consider each cluster as one point in a Grassmann manifold, and measure the geodesic distance among these points. The distances are further analyzed using a min-max algorithm [1] to extract an optimal subset of clusters. Finally, by considering a sparse subgraph of each selected cluster, we detect a representative using principal component centrality [11]. We refer to the proposed representative selection framework as a Sparse Graph and Grassmann Manifold (SGGM) based approach. To validate the proposed SGGM framework, we apply it onto the problem of video summarization where only few video frames, known as key frames, are selected among a much longer video sequence. A comparison of the results obtained by the proposed algorithm with the ground truth, which is agreed by multiple human judges, and with some state-of-the-art methods clearly indicates the viability of the SGGM framework.

Single Image Super Resolution via Manifold Approximation

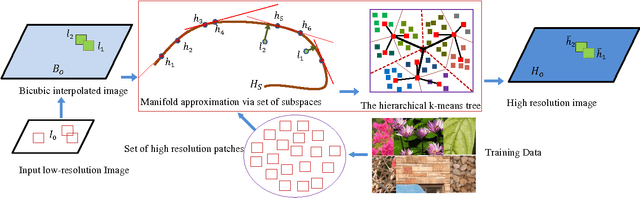
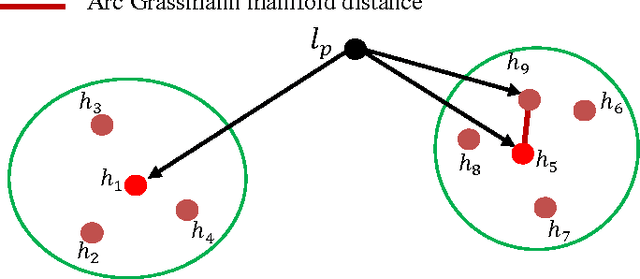
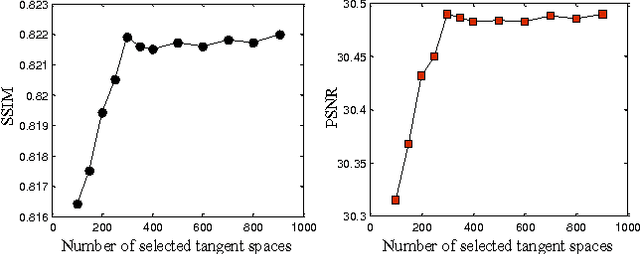
Image super-resolution remains an important research topic to overcome the limitations of physical acquisition systems, and to support the development of high resolution displays. Previous example-based super-resolution approaches mainly focus on analyzing the co-occurrence properties of low resolution and high-resolution patches. Recently, we proposed a novel single image super-resolution approach based on linear manifold approximation of the high-resolution image-patch space [1]. The image super-resolution problem is then formulated as an optimization problem of searching for the best matched high resolution patch in the manifold for a given low-resolution patch. We developed a novel technique based on the l1 norm sparse graph to learn a set of low dimensional affine spaces or tangent subspaces of the high-resolution patch manifold. The optimization problem is then solved based on the learned set of tangent subspaces. In this paper, we build on our recent work as follows. First, we consider and analyze each tangent subspace as one point in a Grassmann manifold, which helps to compute geodesic pairwise distances among these tangent subspaces. Second, we develop a min-max algorithm to select an optimal subset of tangent subspaces. This optimal subset reduces the computational cost while still preserving the quality of the reconstructed high-resolution image. Third, and to further achieve lower computational complexity, we perform hierarchical clustering on the optimal subset based on Grassmann manifold distances. Finally, we analytically prove the validity of the proposed Grassmann-distance based clustering. A comparison of the obtained results with other state-of-the-art methods clearly indicates the viability of the new proposed framework.