Stochastic Neural Network with Kronecker Flow

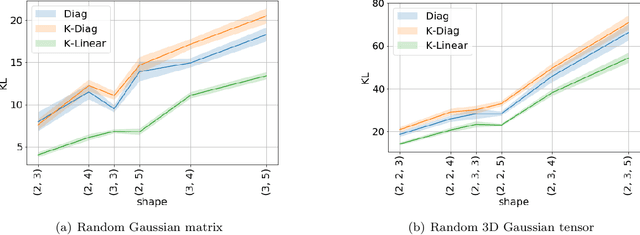
Recent advances in variational inference enable the modelling of highly structured joint distributions, but are limited in their capacity to scale to the high-dimensional setting of stochastic neural networks. This limitation motivates a need for scalable parameterizations of the noise generation process, in a manner that adequately captures the dependencies among the various parameters. In this work, we address this need and present the Kronecker Flow, a generalization of the Kronecker product to invertible mappings designed for stochastic neural networks. We apply our method to variational Bayesian neural networks on predictive tasks, PAC-Bayes generalization bound estimation, and approximate Thompson sampling in contextual bandits. In all setups, our methods prove to be competitive with existing methods and better than the baselines.

Note on the bias and variance of variational inference

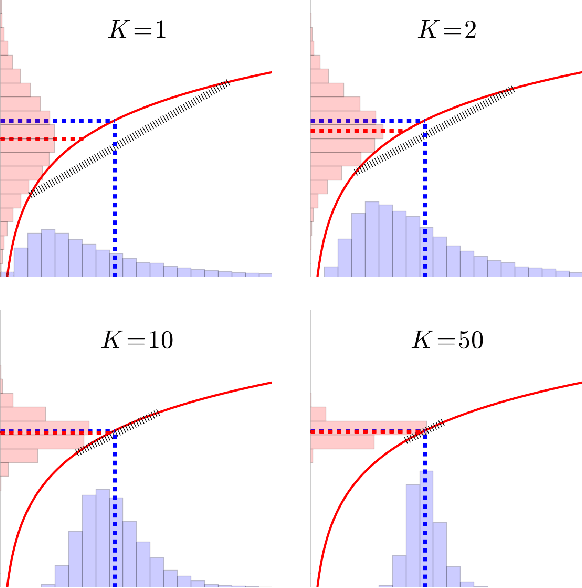
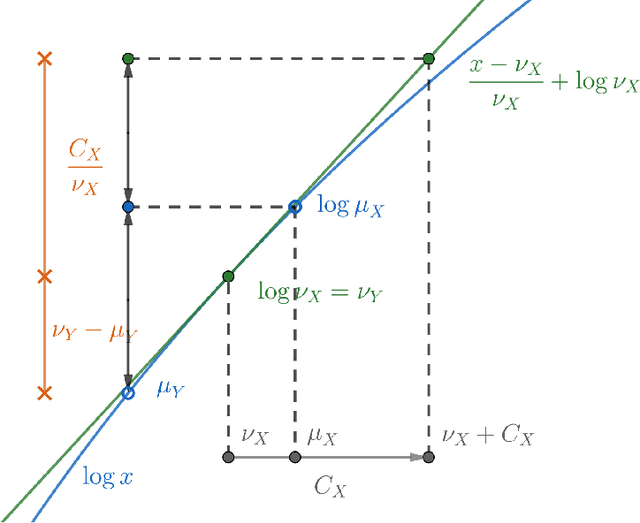
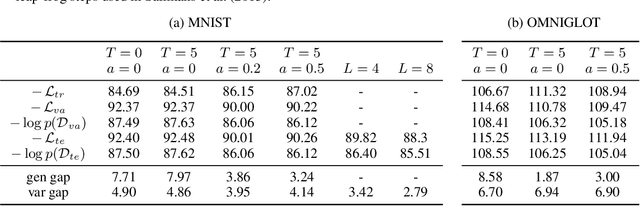
In this note, we study the relationship between the variational gap and the variance of the (log) likelihood ratio. We show that the gap can be upper bounded by some form of dispersion measure of the likelihood ratio, which suggests the bias of variational inference can be reduced by making the distribution of the likelihood ratio more concentrated, such as via averaging and variance reduction.

Hierarchical Importance Weighted Autoencoders

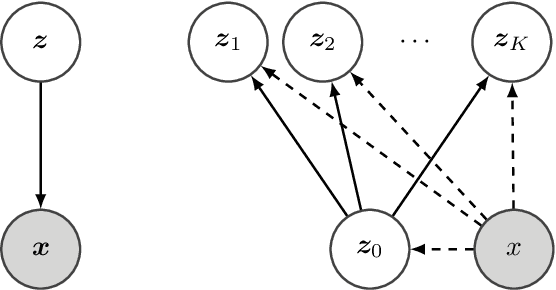
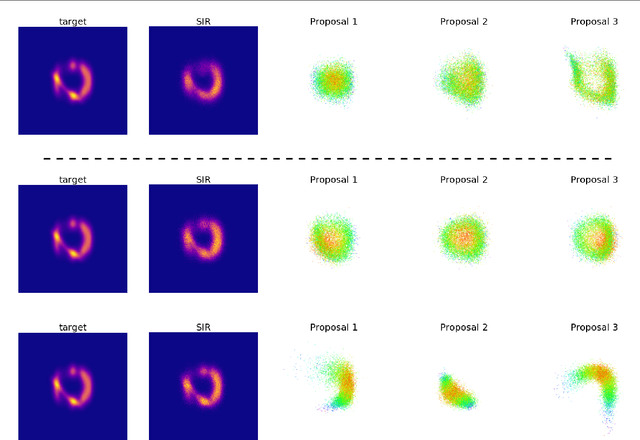
Importance weighted variational inference (Burda et al., 2015) uses multiple i.i.d. samples to have a tighter variational lower bound. We believe a joint proposal has the potential of reducing the number of redundant samples, and introduce a hierarchical structure to induce correlation. The hope is that the proposals would coordinate to make up for the error made by one another to reduce the variance of the importance estimator. Theoretically, we analyze the condition under which convergence of the estimator variance can be connected to convergence of the lower bound. Empirically, we confirm that maximization of the lower bound does implicitly minimize variance. Further analysis shows that this is a result of negative correlation induced by the proposed hierarchical meta sampling scheme, and performance of inference also improves when the number of samples increases.

Improving Explorability in Variational Inference with Annealed Variational Objectives

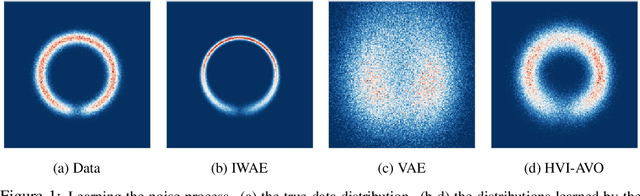
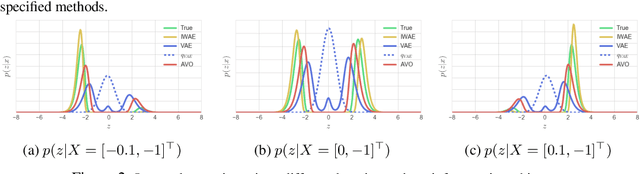
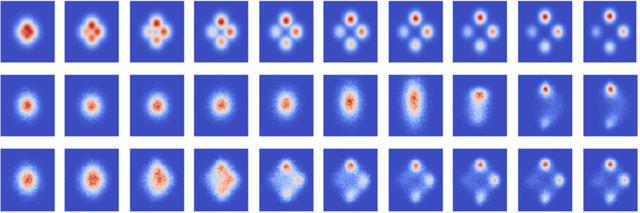
Despite the advances in the representational capacity of approximate distributions for variational inference, the optimization process can still limit the density that is ultimately learned. We demonstrate the drawbacks of biasing the true posterior to be unimodal, and introduce Annealed Variational Objectives (AVO) into the training of hierarchical variational methods. Inspired by Annealed Importance Sampling, the proposed method facilitates learning by incorporating energy tempering into the optimization objective. In our experiments, we demonstrate our method's robustness to deterministic warm up, and the benefits of encouraging exploration in the latent space.

Bayesian Hypernetworks

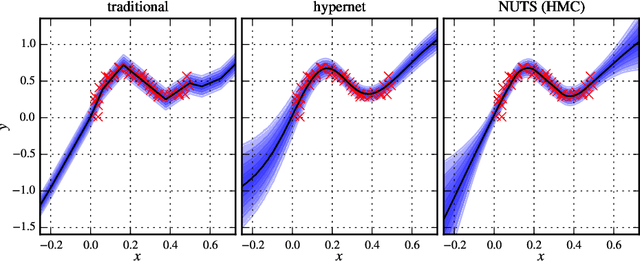
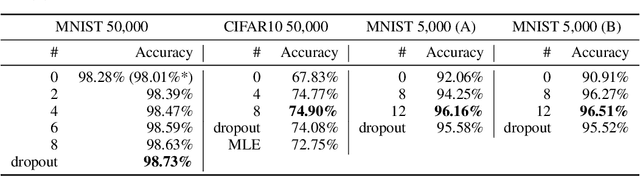
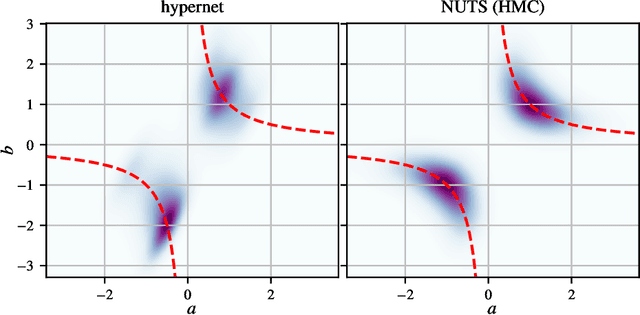
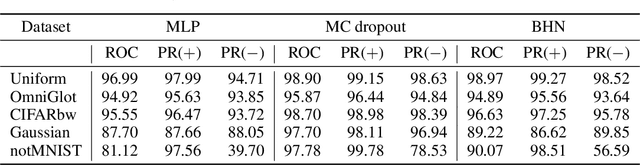
We study Bayesian hypernetworks: a framework for approximate Bayesian inference in neural networks. A Bayesian hypernetwork $\h$ is a neural network which learns to transform a simple noise distribution, $p(\vec\epsilon) = \N(\vec 0,\mat I)$, to a distribution $q(\pp) := q(h(\vec\epsilon))$ over the parameters $\pp$ of another neural network (the "primary network")\@. We train $q$ with variational inference, using an invertible $\h$ to enable efficient estimation of the variational lower bound on the posterior $p(\pp | \D)$ via sampling. In contrast to most methods for Bayesian deep learning, Bayesian hypernets can represent a complex multimodal approximate posterior with correlations between parameters, while enabling cheap iid sampling of~$q(\pp)$. In practice, Bayesian hypernets can provide a better defense against adversarial examples than dropout, and also exhibit competitive performance on a suite of tasks which evaluate model uncertainty, including regularization, active learning, and anomaly detection.

Neural Autoregressive Flows

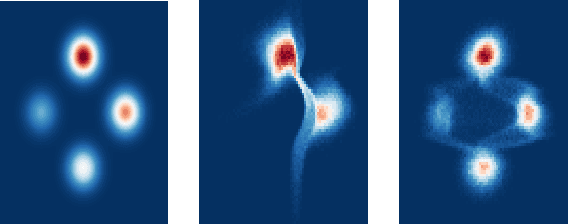
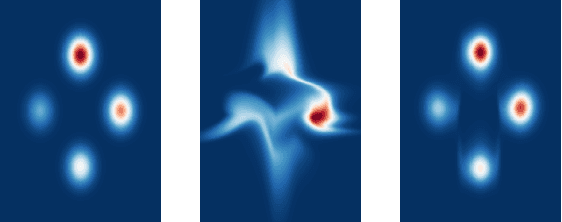
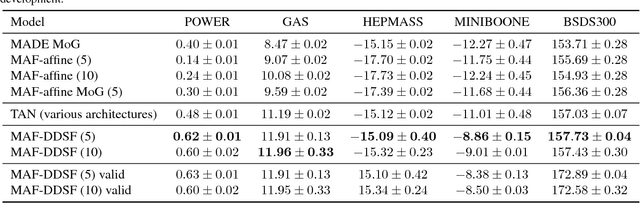
Normalizing flows and autoregressive models have been successfully combined to produce state-of-the-art results in density estimation, via Masked Autoregressive Flows (MAF), and to accelerate state-of-the-art WaveNet-based speech synthesis to 20x faster than real-time, via Inverse Autoregressive Flows (IAF). We unify and generalize these approaches, replacing the (conditionally) affine univariate transformations of MAF/IAF with a more general class of invertible univariate transformations expressed as monotonic neural networks. We demonstrate that the proposed neural autoregressive flows (NAF) are universal approximators for continuous probability distributions, and their greater expressivity allows them to better capture multimodal target distributions. Experimentally, NAF yields state-of-the-art performance on a suite of density estimation tasks and outperforms IAF in variational autoencoders trained on binarized MNIST.

Generating Contradictory, Neutral, and Entailing Sentences

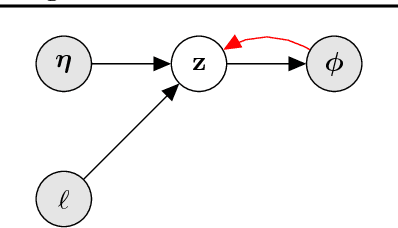
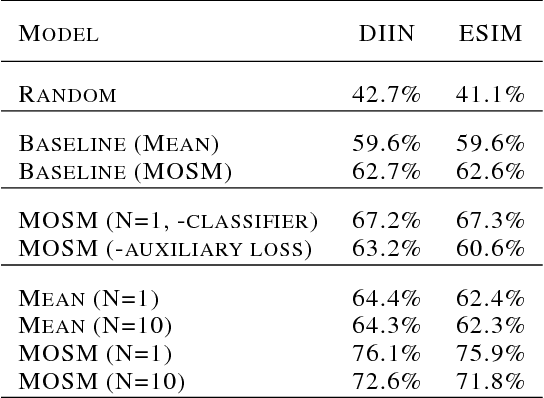
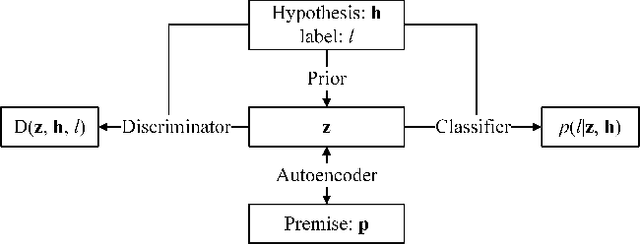
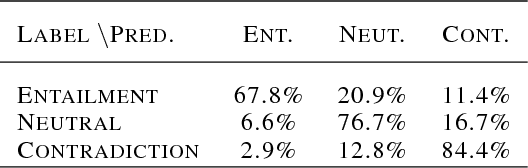
Learning distributed sentence representations remains an interesting problem in the field of Natural Language Processing (NLP). We want to learn a model that approximates the conditional latent space over the representations of a logical antecedent of the given statement. In our paper, we propose an approach to generating sentences, conditioned on an input sentence and a logical inference label. We do this by modeling the different possibilities for the output sentence as a distribution over the latent representation, which we train using an adversarial objective. We evaluate the model using two state-of-the-art models for the Recognizing Textual Entailment (RTE) task, and measure the BLEU scores against the actual sentences as a probe for the diversity of sentences produced by our model. The experiment results show that, given our framework, we have clear ways to improve the quality and diversity of generated sentences.

Neural Language Modeling by Jointly Learning Syntax and Lexicon

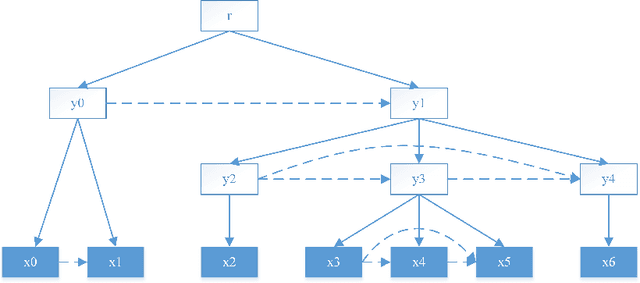
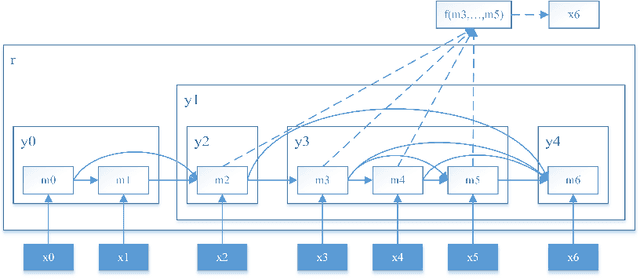
We propose a neural language model capable of unsupervised syntactic structure induction. The model leverages the structure information to form better semantic representations and better language modeling. Standard recurrent neural networks are limited by their structure and fail to efficiently use syntactic information. On the other hand, tree-structured recursive networks usually require additional structural supervision at the cost of human expert annotation. In this paper, We propose a novel neural language model, called the Parsing-Reading-Predict Networks (PRPN), that can simultaneously induce the syntactic structure from unannotated sentences and leverage the inferred structure to learn a better language model. In our model, the gradient can be directly back-propagated from the language model loss into the neural parsing network. Experiments show that the proposed model can discover the underlying syntactic structure and achieve state-of-the-art performance on word/character-level language model tasks.

Learnable Explicit Density for Continuous Latent Space and Variational Inference

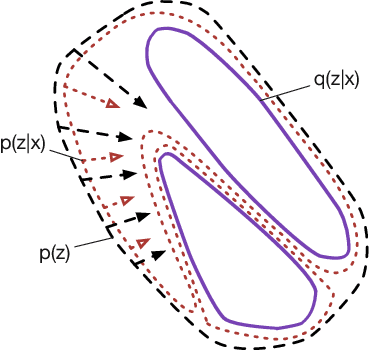
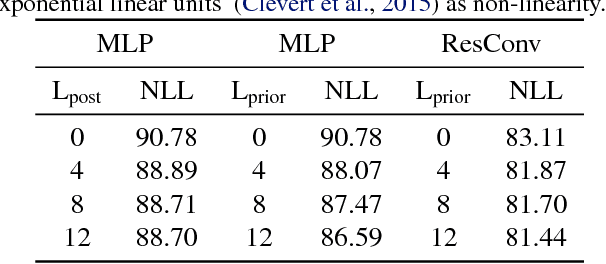
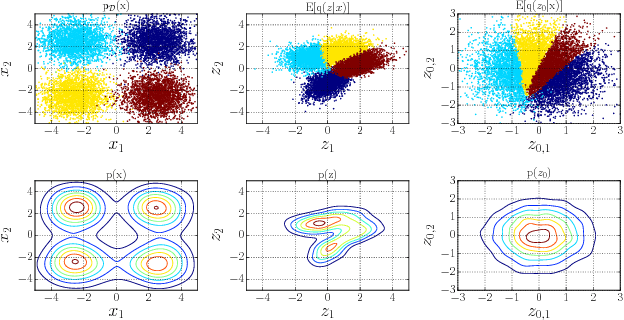
In this paper, we study two aspects of the variational autoencoder (VAE): the prior distribution over the latent variables and its corresponding posterior. First, we decompose the learning of VAEs into layerwise density estimation, and argue that having a flexible prior is beneficial to both sample generation and inference. Second, we analyze the family of inverse autoregressive flows (inverse AF) and show that with further improvement, inverse AF could be used as universal approximation to any complicated posterior. Our analysis results in a unified approach to parameterizing a VAE, without the need to restrict ourselves to use factorial Gaussians in the latent real space.