Machine Learning-Based Modeling of the Anode Heel Effect in X-ray Beam Monte Carlo Simulations

This study enhances Monte Carlo simulation accuracy in X-ray imaging by developing an AI-driven model for the anode heel effect, achieving improved beam intensity distribution and dosimetric precision. Through dynamic adjustments to beam weights on the anode and cathode sides of the X-ray tube, our machine learning model effectively replicates the asymmetry characteristic of clinical X-ray beams. Experimental results reveal dose rate increases of up to 9.6% on the cathode side and reductions of up to 12.5% on the anode side, for energy levels between 50 and 120 kVp. These experimentally optimized beam weights were integrated into the OpenGATE and GGEMS Monte Carlo toolkits, significantly advancing dosimetric simulation accuracy and the image quality which closely resembles the clinical imaging. Validation with fluence and dose actors demonstrated that the AI-based model closely mirrors clinical beam behavior, providing substantial improvements in dose consistency and accuracy over conventional X-ray models. This approach provides a robust framework for improving X-ray dosimetry, with potential applications in dose optimization, imaging quality enhancement, and radiation safety in both clinical and research settings.

PCAAE: Principal Component Analysis Autoencoder for organising the latent space of generative networks

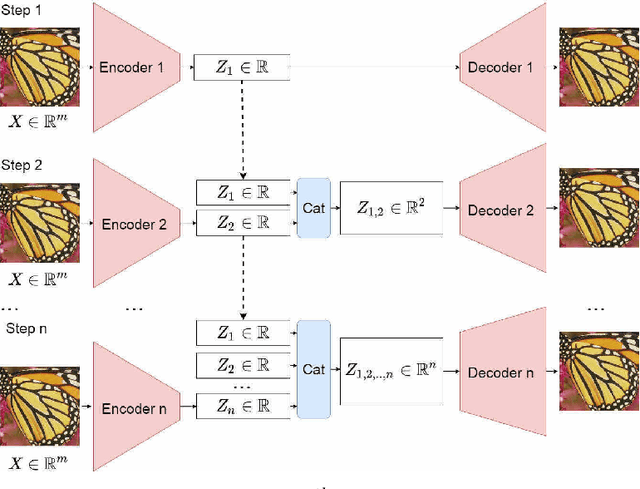
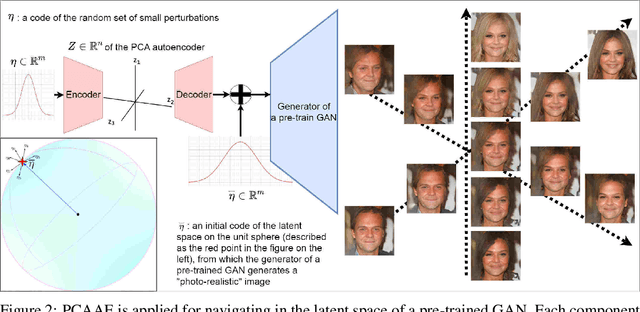
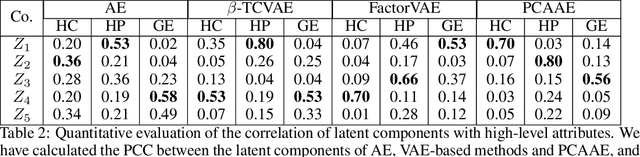
Autoencoders and generative models produce some of the most spectacular deep learning results to date. However, understanding and controlling the latent space of these models presents a considerable challenge. Drawing inspiration from principal component analysis and autoencoder, we propose the Principal Component Analysis Autoencoder (PCAAE). This is a novel autoencoder whose latent space verifies two properties. Firstly, the dimensions are organised in decreasing importance with respect to the data at hand. Secondly, the components of the latent space are statistically independent. We achieve this by progressively increasing the latent space during training, and with a covariance loss applied to the latent codes. The resulting autoencoder produces a latent space which separates the intrinsic attributes of the data into different components of the latent space, in a completely unsupervised manner. We also describe an extension of our approach to the case of powerful, pre-trained GANs. We show results on both synthetic examples of shapes and on a state-of-the-art GAN. For example, we are able to separate the color shade scale of hair and skin, pose of faces and the gender in the CelebA, without accessing any labels. We compare the PCAAE with other state-of-the-art approaches, in particular with respect to the ability to disentangle attributes in the latent space. We hope that this approach will contribute to better understanding of the intrinsic latent spaces of powerful deep generative models.

A PCA-like Autoencoder

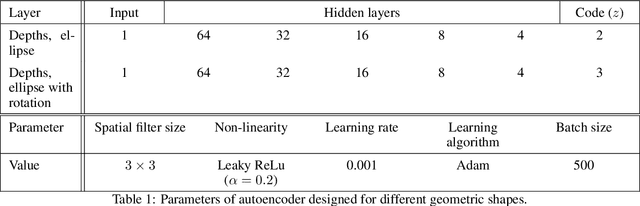
An autoencoder is a neural network which data projects to and from a lower dimensional latent space, where this data is easier to understand and model. The autoencoder consists of two sub-networks, the encoder and the decoder, which carry out these transformations. The neural network is trained such that the output is as close to the input as possible, the data having gone through an information bottleneck : the latent space. This tool bears significant ressemblance to Principal Component Analysis (PCA), with two main differences. Firstly, the autoencoder is a non-linear transformation, contrary to PCA, which makes the autoencoder more flexible and powerful. Secondly, the axes found by a PCA are orthogonal, and are ordered in terms of the amount of variability which the data presents along these axes. This makes the interpretability of the PCA much greater than that of the autoencoder, which does not have these attributes. Ideally, then, we would like an autoencoder whose latent space consists of independent components, ordered by decreasing importance to the data. In this paper, we propose an algorithm to create such a network. We create an iterative algorithm which progressively increases the size of the latent space, learning a new dimension at each step. Secondly, we propose a covariance loss term to add to the standard autoencoder loss function, as well as a normalisation layer just before the latent space, which encourages the latent space components to be statistically independent. We demonstrate the results of this autoencoder on simple geometric shapes, and find that the algorithm indeed finds a meaningful representation in the latent space. This means that subsequent interpolation in the latent space has meaning with respect to the geometric properties of the images.