STO-RL: Offline RL under Sparse Rewards via LLM-Guided Subgoal Temporal Order

Offline reinforcement learning (RL) enables policy learning from pre-collected datasets, avoiding costly and risky online interactions, but it often struggles with long-horizon tasks involving sparse rewards. Existing goal-conditioned and hierarchical offline RL methods decompose such tasks and generate intermediate rewards to mitigate limitations of traditional offline RL, but usually overlook temporal dependencies among subgoals and rely on imprecise reward shaping, leading to suboptimal policies. To address these issues, we propose STO-RL (Offline RL using LLM-Guided Subgoal Temporal Order), an offline RL framework that leverages large language models (LLMs) to generate temporally ordered subgoal sequences and corresponding state-to-subgoal-stage mappings. Using this temporal structure, STO-RL applies potential-based reward shaping to transform sparse terminal rewards into dense, temporally consistent signals, promoting subgoal progress while avoiding suboptimal solutions. The resulting augmented dataset with shaped rewards enables efficient offline training of high-performing policies. Evaluations on four discrete and continuous sparse-reward benchmarks demonstrate that STO-RL consistently outperforms state-of-the-art offline goal-conditioned and hierarchical RL baselines, achieving faster convergence, higher success rates, and shorter trajectories. Ablation studies further confirm STO-RL's robustness to imperfect or noisy LLM-generated subgoal sequences, demonstrating that LLM-guided subgoal temporal structures combined with theoretically grounded reward shaping provide a practical and scalable solution for long-horizon offline RL.

Multi-Task Vehicle Routing Solver via Mixture of Specialized Experts under State-Decomposable MDP

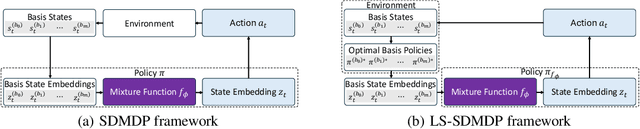
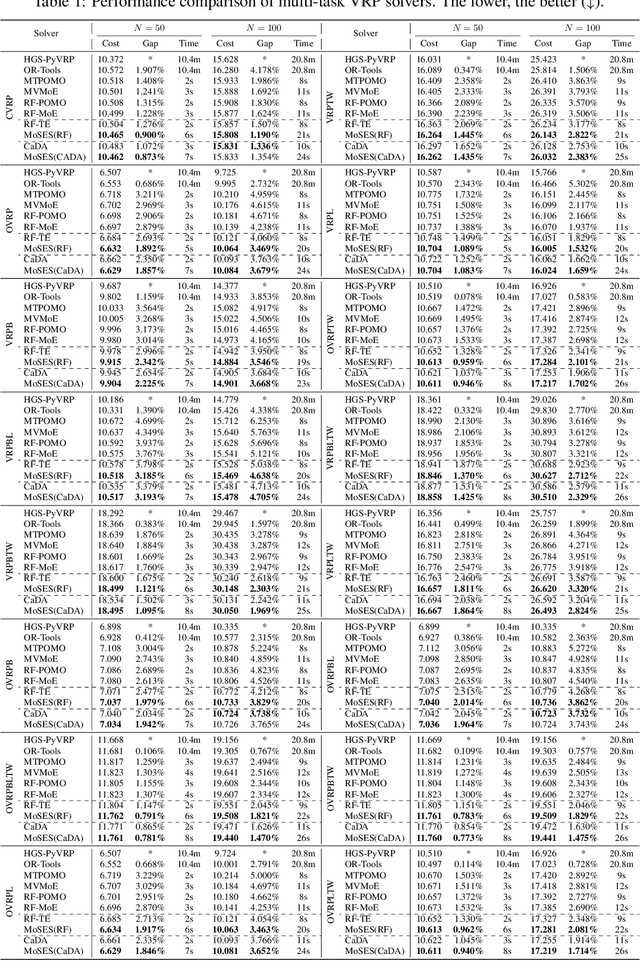
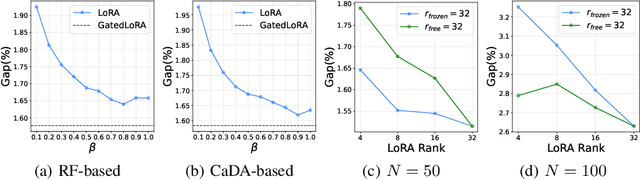
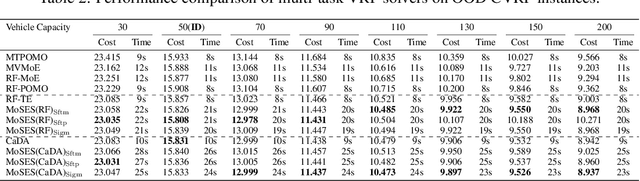
Existing neural methods for multi-task vehicle routing problems (VRPs) typically learn unified solvers to handle multiple constraints simultaneously. However, they often underutilize the compositional structure of VRP variants, each derivable from a common set of basis VRP variants. This critical oversight causes unified solvers to miss out the potential benefits of basis solvers, each specialized for a basis VRP variant. To overcome this limitation, we propose a framework that enables unified solvers to perceive the shared-component nature across VRP variants by proactively reusing basis solvers, while mitigating the exponential growth of trained neural solvers. Specifically, we introduce a State-Decomposable MDP (SDMDP) that reformulates VRPs by expressing the state space as the Cartesian product of basis state spaces associated with basis VRP variants. More crucially, this formulation inherently yields the optimal basis policy for each basis VRP variant. Furthermore, a Latent Space-based SDMDP extension is developed by incorporating both the optimal basis policies and a learnable mixture function to enable the policy reuse in the latent space. Under mild assumptions, this extension provably recovers the optimal unified policy of SDMDP through the mixture function that computes the state embedding as a mapping from the basis state embeddings generated by optimal basis policies. For practical implementation, we introduce the Mixture-of-Specialized-Experts Solver (MoSES), which realizes basis policies through specialized Low-Rank Adaptation (LoRA) experts, and implements the mixture function via an adaptive gating mechanism. Extensive experiments conducted across VRP variants showcase the superiority of MoSES over prior methods.

SEAL: SEmantic-Augmented Imitation Learning via Language Model

Hierarchical Imitation Learning (HIL) is a promising approach for tackling long-horizon decision-making tasks. While it is a challenging task due to the lack of detailed supervisory labels for sub-goal learning, and reliance on hundreds to thousands of expert demonstrations. In this work, we introduce SEAL, a novel framework that leverages Large Language Models (LLMs)'s powerful semantic and world knowledge for both specifying sub-goal space and pre-labeling states to semantically meaningful sub-goal representations without prior knowledge of task hierarchies. SEAL employs a dual-encoder structure, combining supervised LLM-guided sub-goal learning with unsupervised Vector Quantization (VQ) for more robust sub-goal representations. Additionally, SEAL incorporates a transition-augmented low-level planner for improved adaptation to sub-goal transitions. Our experiments demonstrate that SEAL outperforms state-of-the-art HIL methods and LLM-based planning approaches, particularly in settings with small expert datasets and complex long-horizon tasks.

Learning and Optimization for Price-based Demand Response of Electric Vehicle Charging

In the context of charging electric vehicles (EVs), the price-based demand response (PBDR) is becoming increasingly significant for charging load management. Such response usually encourages cost-sensitive customers to adjust their energy demand in response to changes in price for financial incentives. Thus, to model and optimize EV charging, it is important for charging station operator to model the PBDR patterns of EV customers by precisely predicting charging demands given price signals. Then the operator refers to these demands to optimize charging station power allocation policy. The standard pipeline involves offline fitting of a PBDR function based on historical EV charging records, followed by applying estimated EV demands in downstream charging station operation optimization. In this work, we propose a new decision-focused end-to-end framework for PBDR modeling that combines prediction errors and downstream optimization cost errors in the model learning stage. We evaluate the effectiveness of our method on a simulation of charging station operation with synthetic PBDR patterns of EV customers, and experimental results demonstrate that this framework can provide a more reliable prediction model for the ultimate optimization process, leading to more effective optimization solutions in terms of cost savings and charging station operation objectives with only a few training samples.

Pontryagin Optimal Controller via Neural Networks

Solving real-world optimal control problems are challenging tasks, as the system dynamics can be highly non-linear or including nonconvex objectives and constraints, while in some cases the dynamics are unknown, making it hard to numerically solve the optimal control actions. To deal with such modeling and computation challenges, in this paper, we integrate Neural Networks with the Pontryagin's Minimum Principle (PMP), and propose a computationally efficient framework NN-PMP. The resulting controller can be implemented for systems with unknown and complex dynamics. It can not only utilize the accurate surrogate models parameterized by neural networks, but also efficiently recover the optimality conditions along with the optimal action sequences via PMP conditions. A toy example on a nonlinear Martian Base operation along with a real-world lossy energy storage arbitrage example demonstrates our proposed NN-PMP is a general and versatile computation tool for finding optimal solutions. Compared with solutions provided by the numerical optimization solver with approximated linear dynamics, NN-PMP achieves more efficient system modeling and higher performance in terms of control objectives.