Physics-Informed Machine Learning for Two-Phase Moving-Interface and Stefan Problems

The Stefan problem is a classical free-boundary problem that models phase-change processes and poses computational challenges due to its moving interface and nonlinear temperature-phase coupling. In this work, we develop a physics-informed neural network framework for solving two-phase Stefan problems. The proposed method explicitly tracks the interface motion and enforces the discontinuity in the temperature gradient across the interface while maintaining global consistency of the temperature field. Our approach employs two neural networks: one representing the moving interface and the other for the temperature field. The interface network allows rapid categorization of thermal diffusivity in the spatial domain, which is a crucial step for selecting training points for the temperature network. The temperature network's input is augmented with a modified zero-level set function to accurately capture the jump in its normal derivative across the interface. Numerical experiments on two-phase dynamical Stefan problems demonstrate the superior accuracy and effectiveness of our proposed method compared with the ones obtained by other neural network methodology in literature. The results indicate that the proposed framework offers a robust and flexible alternative to traditional numerical methods for solving phase-change problems governed by moving boundaries. In addition, the proposed method can capture an unstable interface evolution associated with the Mullins-Sekerka instability.

Consistency Training with Physical Constraints

We propose a physics-aware Consistency Training (CT) method that accelerates sampling in Diffusion Models with physical constraints. Our approach leverages a two-stage strategy: (1) learning the noise-to-data mapping via CT, and (2) incorporating physics constraints as a regularizer. Experiments on toy examples show that our method generates samples in a single step while adhering to the imposed constraints. This approach has the potential to efficiently solve partial differential equations (PDEs) using deep generative modeling.

A Shallow Ritz Method for elliptic problems with Singular Sources

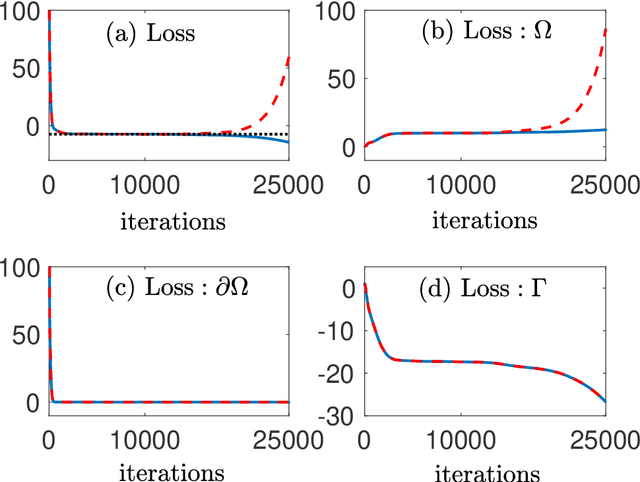
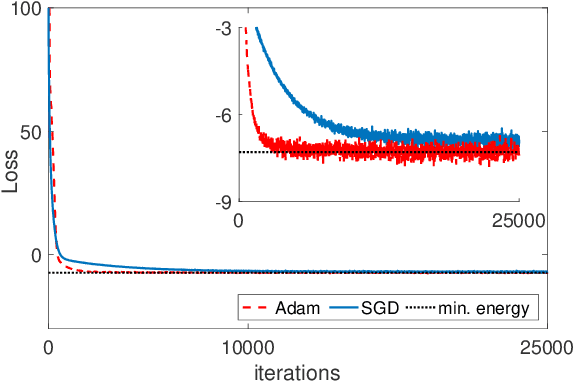
In this paper, a shallow Ritz-type neural network for solving elliptic problems with delta function singular sources on an interface is developed. There are three novel features in the present work; namely, (i) the delta function singularity is naturally removed, (ii) level set function is introduced as a feather input, (iii) it is completely shallow consisting of only one hidden layer. We first introduce the energy functional of the problem and then transform the contribution of singular sources to a regular surface integral along the interface. In such a way the delta function singularity can be naturally removed without the introduction of discrete delta function that is commonly used in traditional regularization methods such as the well-known immersed boundary method. The original problem is then reformulated as a minimization problem. We propose a shallow Ritz-type neural network with one hidden layer to approximate the global minimizer of the energy functional. As a result, the network is trained by minimizing the loss function that is a discrete version of the energy. In addition, we include the level set function of the interface as a feature input and find that it significantly improves the training efficiency and accuracy. We perform a series of numerical tests to demonstrate the accuracy of the present network as well as its capability for problems in irregular domains and in higher dimensions.

Mitigating Asymmetric Nonlinear Weight Update Effects in Hardware Neural Network based on Analog Resistive Synapse

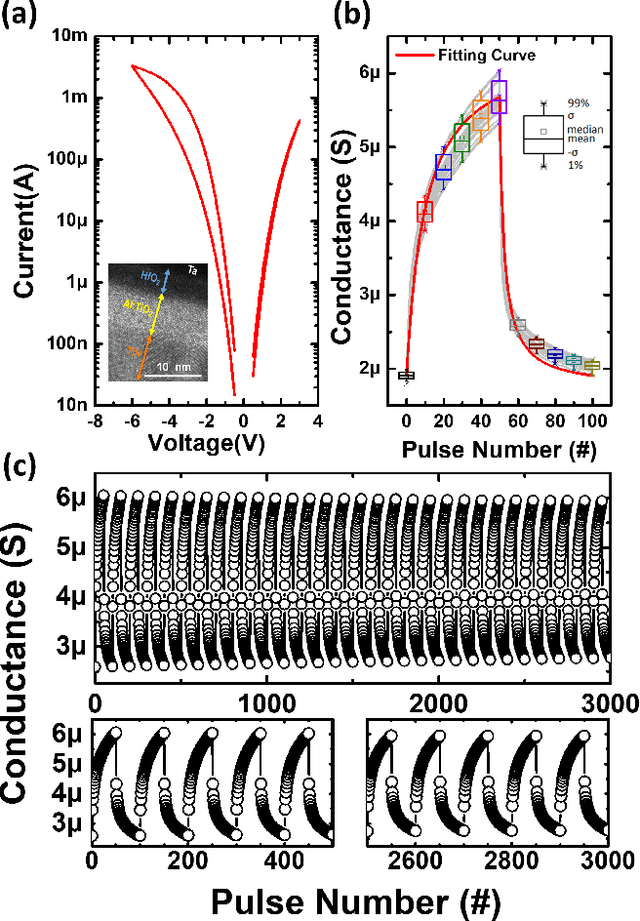
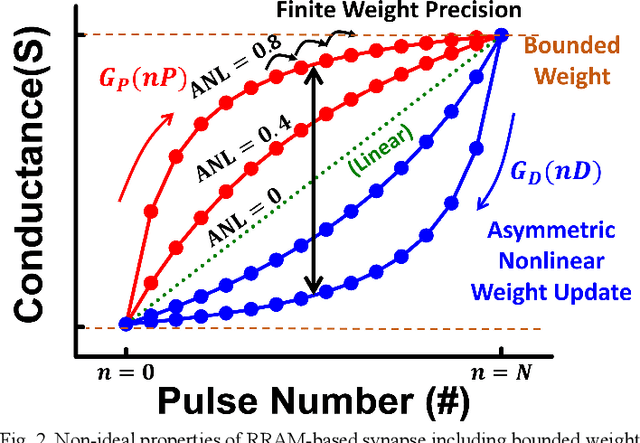
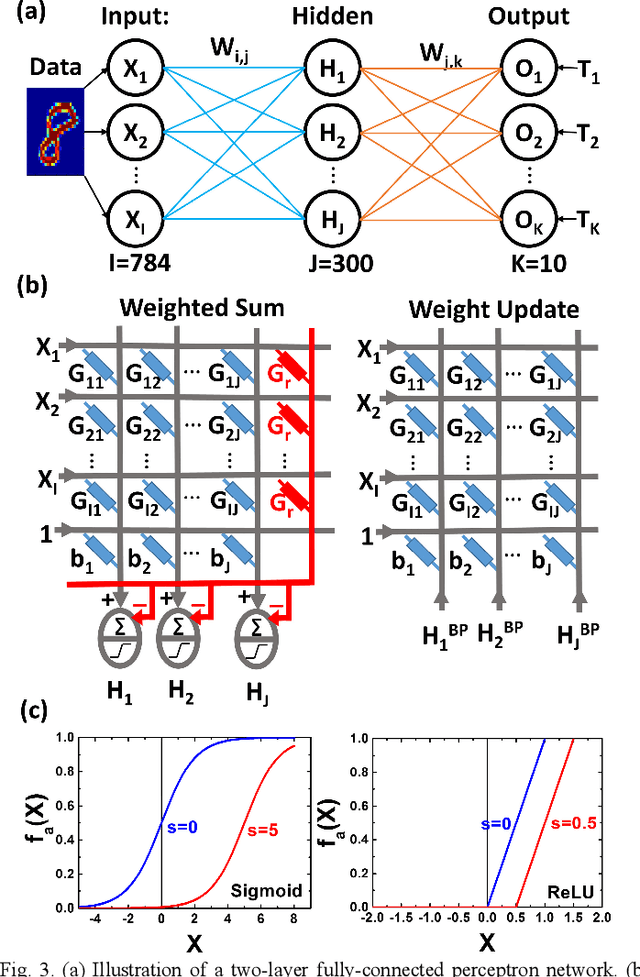
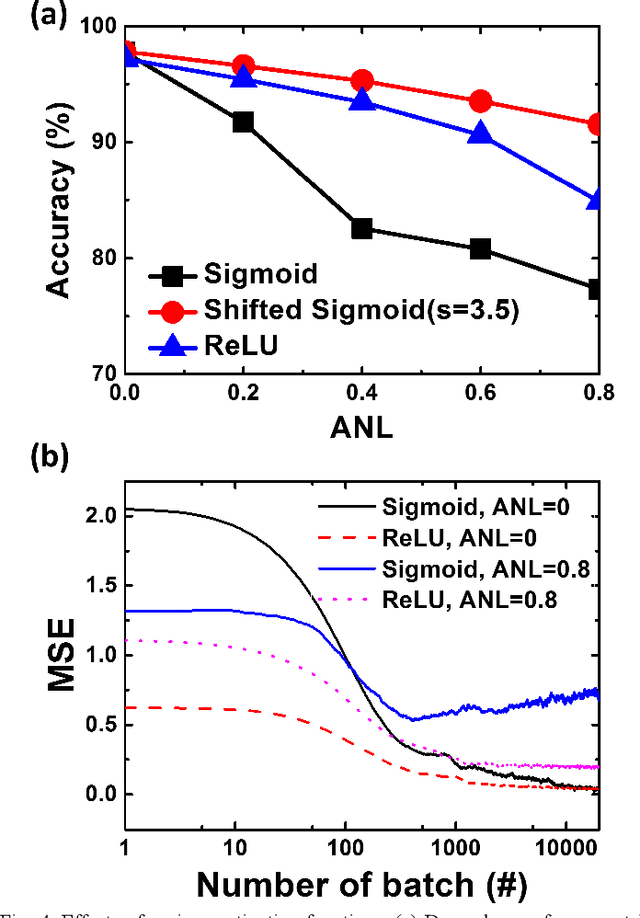
Asymmetric nonlinear weight update is considered as one of the major obstacles for realizing hardware neural networks based on analog resistive synapses because it significantly compromises the online training capability. This paper provides new solutions to this critical issue through co-optimization with the hardware-applicable deep-learning algorithms. New insights on engineering activation functions and a threshold weight update scheme effectively suppress the undesirable training noise induced by inaccurate weight update. We successfully trained a two-layer perceptron network online and improved the classification accuracy of MNIST handwritten digit dataset to 87.8/94.8% by using 6-bit/8-bit analog synapses, respectively, with extremely high asymmetric nonlinearity.