Synthetic Data for Portfolios: A Throw of the Dice Will Never Abolish Chance

Simulation methods have always been instrumental in finance, and data-driven methods with minimal model specification, commonly referred to as generative models, have attracted increasing attention, especially after the success of deep learning in a broad range of fields. However, the adoption of these models in financial applications has not kept pace with the growing interest, probably due to the unique complexities and challenges of financial markets. This paper aims to contribute to a deeper understanding of the limitations of generative models, particularly in portfolio and risk management. To this end, we begin by presenting theoretical results on the importance of initial sample size, and point out the potential pitfalls of generating far more data than originally available. We then highlight the inseparable nature of model development and the desired use case by touching on a paradox: generic generative models inherently care less about what is important for constructing portfolios (in particular the long-short ones). Based on these findings, we propose a pipeline for the generation of multivariate returns that meets conventional evaluation standards on a large universe of US equities while being compliant with stylized facts observed in asset returns and turning around the pitfalls we previously identified. Moreover, we insist on the need for more delicate evaluation methods, and suggest, through an example of mean-reversion strategies, a method designed to identify poor models for a given application based on regurgitative training, i.e. retraining the model using the data it has itself generated, which is commonly referred to in statistics as identifiability.

Learning a functional control for high-frequency finance

We use a deep neural network to generate controllers for optimal trading on high frequency data. For the first time, a neural network learns the mapping between the preferences of the trader, i.e. risk aversion parameters, and the optimal controls. An important challenge in learning this mapping is that in intraday trading, trader's actions influence price dynamics in closed loop via the market impact. The exploration--exploitation tradeoff generated by the efficient execution is addressed by tuning the trader's preferences to ensure long enough trajectories are produced during the learning phase. The issue of scarcity of financial data is solved by transfer learning: the neural network is first trained on trajectories generated thanks to a Monte-Carlo scheme, leading to a good initialization before training on historical trajectories. Moreover, to answer to genuine requests of financial regulators on the explainability of machine learning generated controls, we project the obtained "blackbox controls" on the space usually spanned by the closed-form solution of the stylized optimal trading problem, leading to a transparent structure. For more realistic loss functions that have no closed-form solution, we show that the average distance between the generated controls and their explainable version remains small. This opens the door to the acceptance of ML-generated controls by financial regulators.

Improving reinforcement learning algorithms: towards optimal learning rate policies

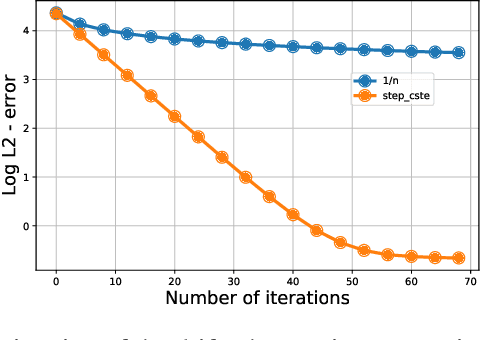
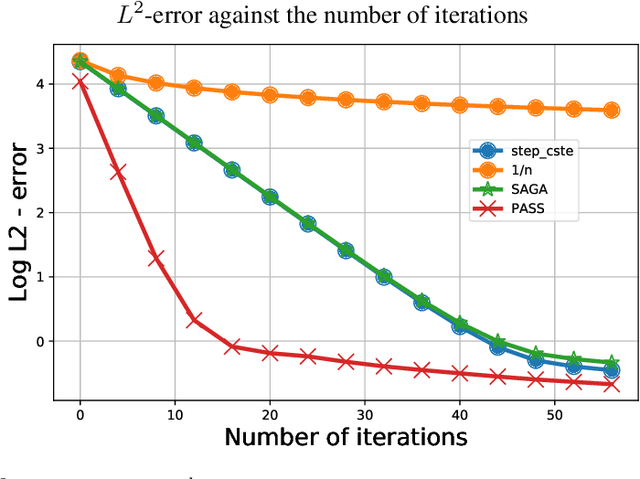
This paper investigates to what extent we can improve reinforcement learning algorithms. Our study is split in three parts. First, our analysis shows that the classical asymptotic convergence rate $O(1/\sqrt{N})$ is pessimistic and can be replaced by $O((\log(N)/N)^{\beta})$ with $\frac{1}{2}\leq \beta \leq 1$ and $N$ the number of iterations. Second, we propose a dynamic optimal policy for the choice of the learning rate $(\gamma_k)_{k\geq 0}$ used in stochastic algorithms. We decompose our policy into two interacting levels: the inner and the outer level. In the inner level, we present the PASS algorithm (for "PAst Sign Search") which, based on a predefined sequence $(\gamma^o_k)_{k\geq 0}$, constructs a new sequence $(\gamma^i_k)_{k\geq 0}$ whose error decreases faster. In the outer level, we propose an optimal methodology for the selection of the predefined sequence $(\gamma^o_k)_{k\geq 0}$. Third, we show empirically that our selection methodology of the learning rate outperforms significantly standard algorithms used in reinforcement learning (RL) in the three following applications: the estimation of a drift, the optimal placement of limit orders and the optimal execution of large number of shares.