Decision Making under Model Misspecification: DRO with Robust Bayesian Ambiguity Sets

Distributionally Robust Optimisation (DRO) protects risk-averse decision-makers by considering the worst-case risk within an ambiguity set of distributions based on the empirical distribution or a model. To further guard against finite, noisy data, model-based approaches admit Bayesian formulations that propagate uncertainty from the posterior to the decision-making problem. However, when the model is misspecified, the decision maker must stretch the ambiguity set to contain the data-generating process (DGP), leading to overly conservative decisions. We address this challenge by introducing DRO with Robust, to model misspecification, Bayesian Ambiguity Sets (DRO-RoBAS). These are Maximum Mean Discrepancy ambiguity sets centred at a robust posterior predictive distribution that incorporates beliefs about the DGP. We show that the resulting optimisation problem obtains a dual formulation in the Reproducing Kernel Hilbert Space and we give probabilistic guarantees on the tolerance level of the ambiguity set. Our method outperforms other Bayesian and empirical DRO approaches in out-of-sample performance on the Newsvendor and Portfolio problems with various cases of model misspecification.

Decision Making under the Exponential Family: Distributionally Robust Optimisation with Bayesian Ambiguity Sets

Decision making under uncertainty is challenging as the data-generating process (DGP) is often unknown. Bayesian inference proceeds by estimating the DGP through posterior beliefs on the model's parameters. However, minimising the expected risk under these beliefs can lead to suboptimal decisions due to model uncertainty or limited, noisy observations. To address this, we introduce Distributionally Robust Optimisation with Bayesian Ambiguity Sets (DRO-BAS) which hedges against model uncertainty by optimising the worst-case risk over a posterior-informed ambiguity set. We provide two such sets, based on posterior expectations (DRO-BAS(PE)) or posterior predictives (DRO-BAS(PP)) and prove that both admit, under conditions, strong dual formulations leading to efficient single-stage stochastic programs which are solved with a sample average approximation. For DRO-BAS(PE) this covers all conjugate exponential family members while for DRO-BAS(PP) this is shown under conditions on the predictive's moment generating function. Our DRO-BAS formulations Pareto dominate existing Bayesian DRO on the Newsvendor problem and achieve faster solve times with comparable robustness on the Portfolio problem.

Distributionally Robust Optimisation with Bayesian Ambiguity Sets

Decision making under uncertainty is challenging since the data-generating process (DGP) is often unknown. Bayesian inference proceeds by estimating the DGP through posterior beliefs about the model's parameters. However, minimising the expected risk under these posterior beliefs can lead to sub-optimal decisions due to model uncertainty or limited, noisy observations. To address this, we introduce Distributionally Robust Optimisation with Bayesian Ambiguity Sets (DRO-BAS) which hedges against uncertainty in the model by optimising the worst-case risk over a posterior-informed ambiguity set. We show that our method admits a closed-form dual representation for many exponential family members and showcase its improved out-of-sample robustness against existing Bayesian DRO methodology in the Newsvendor problem.

Robust Bayesian Inference for Measurement Error Models

Measurement error occurs when a set of covariates influencing a response variable are corrupted by noise. This can lead to misleading inference outcomes, particularly in problems where accurately estimating the relationship between covariates and response variables is crucial, such as causal effect estimation. Existing methods for dealing with measurement error often rely on strong assumptions such as knowledge of the error distribution or its variance and availability of replicated measurements of the covariates. We propose a Bayesian Nonparametric Learning framework which is robust to mismeasured covariates, does not require the preceding assumptions, and is able to incorporate prior beliefs about the true error distribution. Our approach gives rise to two methods that are robust to measurement error via different loss functions: one based on the Total Least Squares objective and the other based on Maximum Mean Discrepancy (MMD). The latter allows for generalisation to non-Gaussian distributed errors and non-linear covariate-response relationships. We provide bounds on the generalisation error using the MMD-loss and showcase the effectiveness of the proposed framework versus prior art in real-world mental health and dietary datasets that contain significant measurement errors.

Robust Bayesian Inference for Simulator-based Models via the MMD Posterior Bootstrap

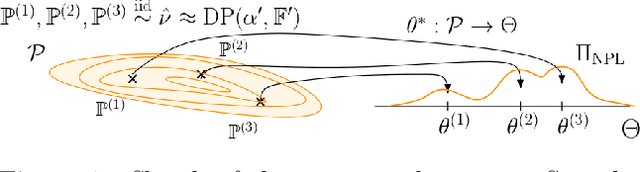
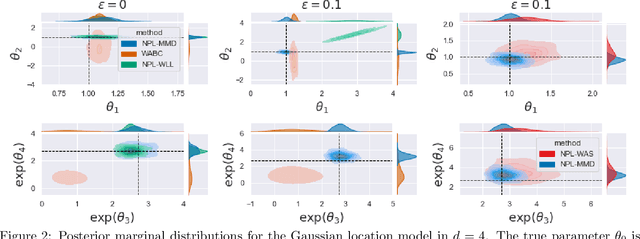
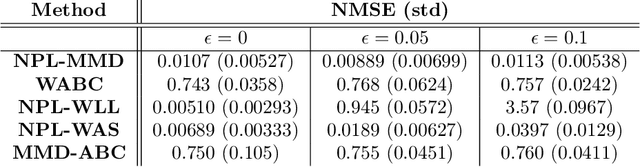
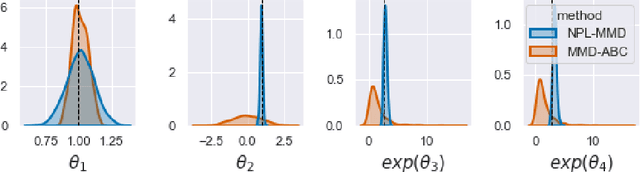
Simulator-based models are models for which the likelihood is intractable but simulation of synthetic data is possible. They are often used to describe complex real-world phenomena, and as such can often be misspecified in practice. Unfortunately, existing Bayesian approaches for simulators are known to perform poorly in those cases. In this paper, we propose a novel algorithm based on the posterior bootstrap and maximum mean discrepancy estimators. This leads to a highly-parallelisable Bayesian inference algorithm with strong robustness properties. This is demonstrated through an in-depth theoretical study which includes generalisation bounds and proofs of frequentist consistency and robustness of our posterior. The approach is then assessed on a range of examples including a g-and-k distribution and a toggle-switch model.