How Can Increased Randomness in Stochastic Gradient Descent Improve Generalization?

Recent works report that increasing the learning rate or decreasing the minibatch size in stochastic gradient descent (SGD) can improve test set performance. We argue this is expected under some conditions in models with a loss function with multiple local minima. Our main contribution is an approximate but analytical approach inspired by methods in Physics to study the role of the SGD learning rate and batch size in generalization. We characterize test set performance under a shift between the training and test data distributions for loss functions with multiple minima. The shift can simply be due to sampling, and is therefore typically present in practical applications. We show that the resulting shift in local minima worsens test performance by picking up curvature, implying that generalization improves by selecting wide and/or little-shifted local minima. We then specialize to SGD, and study its test performance under stationarity. Because obtaining the exact stationary distribution of SGD is intractable, we derive a Fokker-Planck approximation of SGD and obtain its stationary distribution instead. This process shows that the learning rate divided by the minibatch size plays a role analogous to temperature in statistical mechanics, and implies that SGD, including its stationary distribution, is largely invariant to changes in learning rate or batch size that leave its temperature constant. We show that increasing SGD temperature encourages the selection of local minima with lower curvature, and can enable better generalization. We provide experiments on CIFAR10 demonstrating the temperature invariance of SGD, improvement of the test loss as SGD temperature increases, and quantifying the impact of sampling versus domain shift in driving this effect. Finally, we present synthetic experiments showing how our theory applies in a simplified loss with two local minima.

The decoupled extended Kalman filter for dynamic exponential-family factorization models

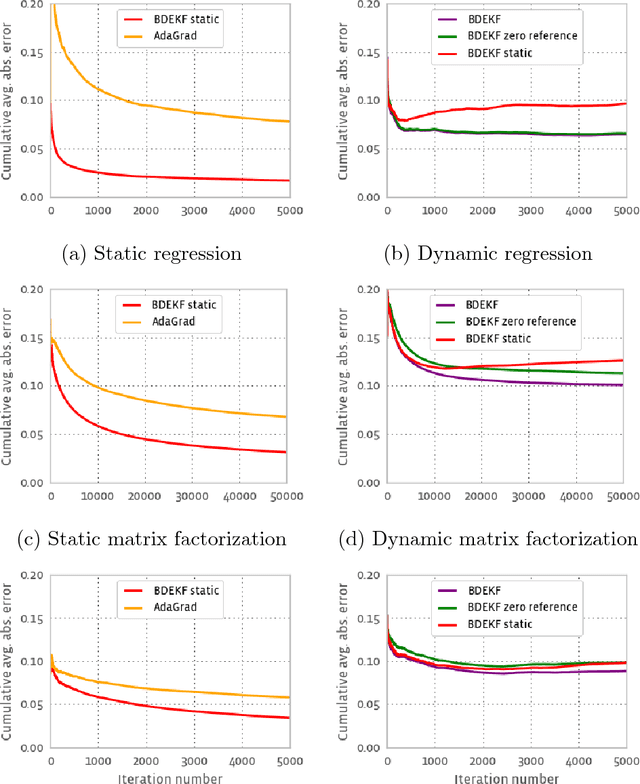
We specialize the decoupled extended Kalman filter (DEKF) for online parameter learning in factorization models, including factorization machines, matrix and tensor factorization, and illustrate the effectiveness of the approach through simulations. Learning model parameters through the DEKF makes factorization models more broadly useful by allowing for more flexible observations through the entire exponential family, modeling parameter drift, and producing parameter uncertainty estimates that can enable explore/exploit and other applications. We use a more general dynamics of the parameters than the standard DEKF, allowing parameter drift while encouraging reasonable values. We also present an alternate derivation of the regular extended Kalman filter and DEKF that connects these methods to natural gradient methods, and suggests a similarly decoupled version of the iterated extended Kalman filter.

Online Algorithms For Parameter Mean And Variance Estimation In Dynamic Regression Models

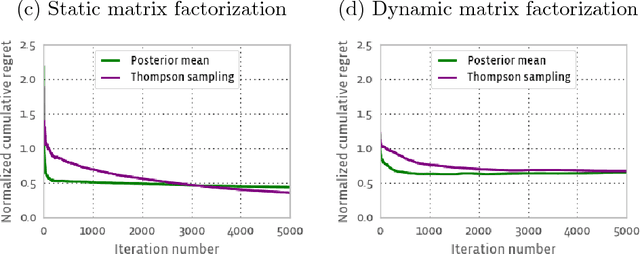
We study the problem of estimating the parameters of a regression model from a set of observations, each consisting of a response and a predictor. The response is assumed to be related to the predictor via a regression model of unknown parameters. Often, in such models the parameters to be estimated are assumed to be constant. Here we consider the more general scenario where the parameters are allowed to evolve over time, a more natural assumption for many applications. We model these dynamics via a linear update equation with additive noise that is often used in a wide range of engineering applications, particularly in the well-known and widely used Kalman filter (where the system state it seeks to estimate maps to the parameter values here). We derive an approximate algorithm to estimate both the mean and the variance of the parameter estimates in an online fashion for a generic regression model. This algorithm turns out to be equivalent to the extended Kalman filter. We specialize our algorithm to the multivariate exponential family distribution to obtain a generalization of the generalized linear model (GLM). Because the common regression models encountered in practice such as logistic, exponential and multinomial all have observations modeled through an exponential family distribution, our results are used to easily obtain algorithms for online mean and variance parameter estimation for all these regression models in the context of time-dependent parameters. Lastly, we propose to use these algorithms in the contextual multi-armed bandit scenario, where so far model parameters are assumed static and observations univariate and Gaussian or Bernoulli. Both of these restrictions can be relaxed using the algorithms described here, which we combine with Thompson sampling to show the resulting performance on a simulation.