Modularity Component Analysis versus Principal Component Analysis

In this paper the exact linear relation between the leading eigenvectors of the modularity matrix and the singular vectors of an uncentered data matrix is developed. Based on this analysis the concept of a modularity component is defined, and its properties are developed. It is shown that modularity component analysis can be used to cluster data similar to how traditional principal component analysis is used except that modularity component analysis does not require data centering.

Relations Between Adjacency and Modularity Graph Partitioning

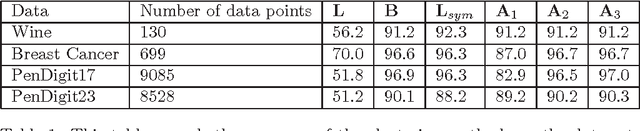
In this paper the exact linear relation between the leading eigenvector of the unnormalized modularity matrix and the eigenvectors of the adjacency matrix is developed. Based on this analysis a method to approximate the leading eigenvector of the modularity matrix is given, and the relative error of the approximation is derived. A complete proof of the equivalence between normalized modularity clustering and normalized adjacency clustering is also given. A new metric is defined to describe the agreement of two clustering methods, and some applications and experiments are given to illustrate and corroborate the points that are made in the theoretical development.

A Case Study in Text Mining: Interpreting Twitter Data From World Cup Tweets

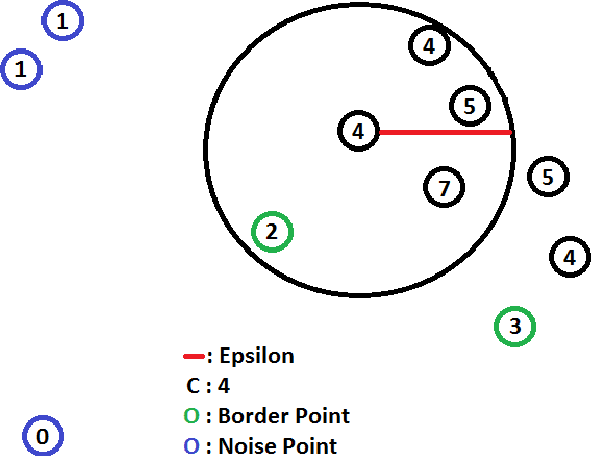
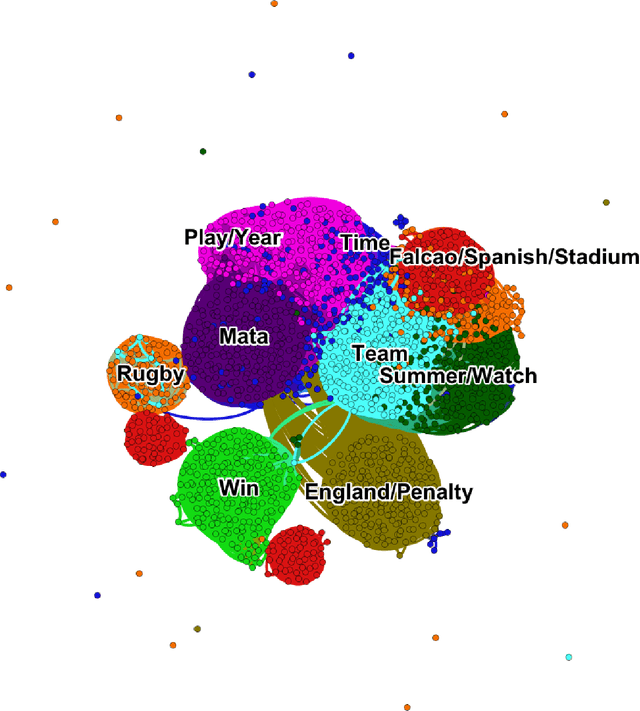
Cluster analysis is a field of data analysis that extracts underlying patterns in data. One application of cluster analysis is in text-mining, the analysis of large collections of text to find similarities between documents. We used a collection of about 30,000 tweets extracted from Twitter just before the World Cup started. A common problem with real world text data is the presence of linguistic noise. In our case it would be extraneous tweets that are unrelated to dominant themes. To combat this problem, we created an algorithm that combined the DBSCAN algorithm and a consensus matrix. This way we are left with the tweets that are related to those dominant themes. We then used cluster analysis to find those topics that the tweets describe. We clustered the tweets using k-means, a commonly used clustering algorithm, and Non-Negative Matrix Factorization (NMF) and compared the results. The two algorithms gave similar results, but NMF proved to be faster and provided more easily interpreted results. We explored our results using two visualization tools, Gephi and Wordle.

A Flexible Iterative Framework for Consensus Clustering

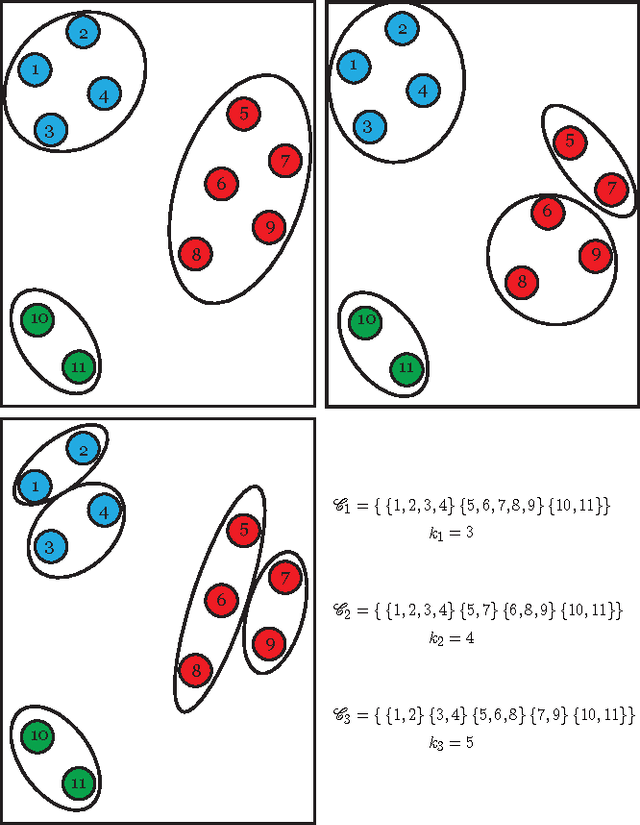
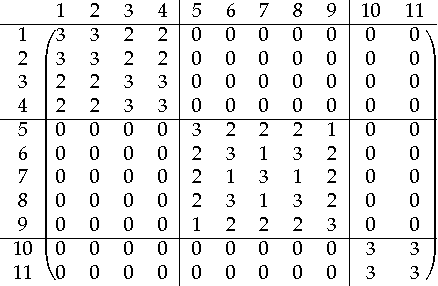
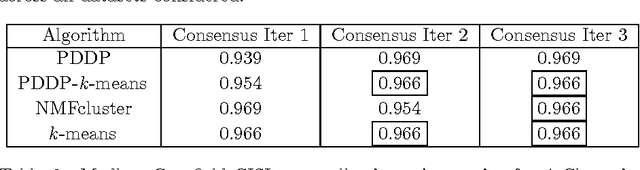
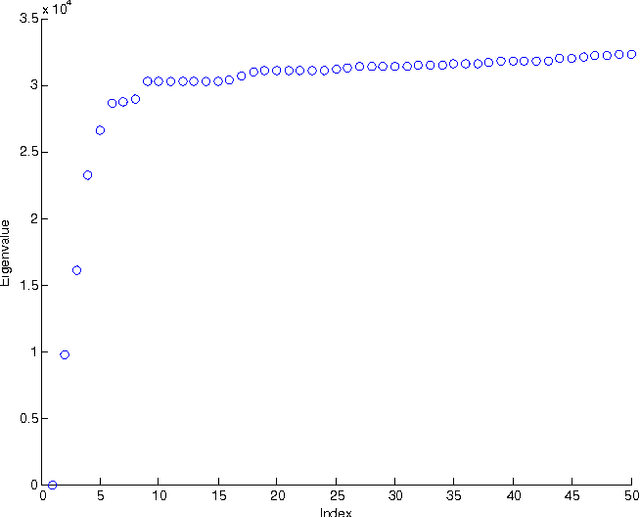
A novel framework for consensus clustering is presented which has the ability to determine both the number of clusters and a final solution using multiple algorithms. A consensus similarity matrix is formed from an ensemble using multiple algorithms and several values for k. A variety of dimension reduction techniques and clustering algorithms are considered for analysis. For noisy or high-dimensional data, an iterative technique is presented to refine this consensus matrix in way that encourages algorithms to agree upon a common solution. We utilize the theory of nearly uncoupled Markov chains to determine the number, k , of clusters in a dataset by considering a random walk on the graph defined by the consensus matrix. The eigenvalues of the associated transition probability matrix are used to determine the number of clusters. This method succeeds at determining the number of clusters in many datasets where previous methods fail. On every considered dataset, our consensus method provides a final result with accuracy well above the average of the individual algorithms.

Determining the Number of Clusters via Iterative Consensus Clustering

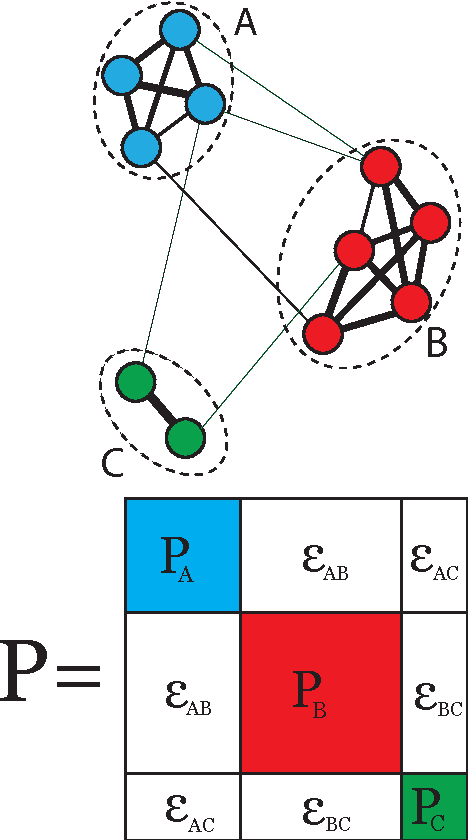
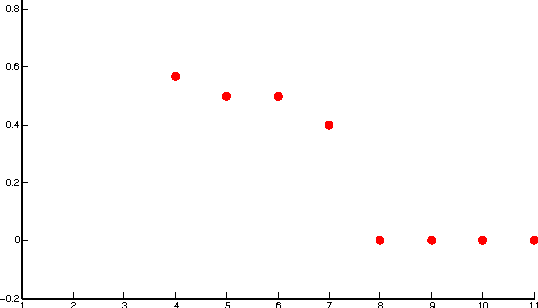
We use a cluster ensemble to determine the number of clusters, k, in a group of data. A consensus similarity matrix is formed from the ensemble using multiple algorithms and several values for k. A random walk is induced on the graph defined by the consensus matrix and the eigenvalues of the associated transition probability matrix are used to determine the number of clusters. For noisy or high-dimensional data, an iterative technique is presented to refine this consensus matrix in way that encourages a block-diagonal form. It is shown that the resulting consensus matrix is generally superior to existing similarity matrices for this type of spectral analysis.

Data Clustering via Principal Direction Gap Partitioning

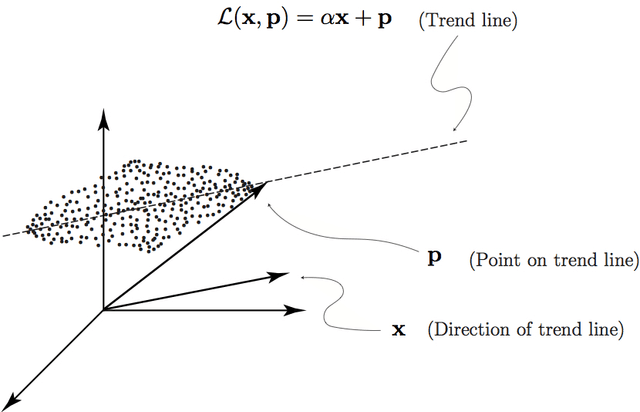
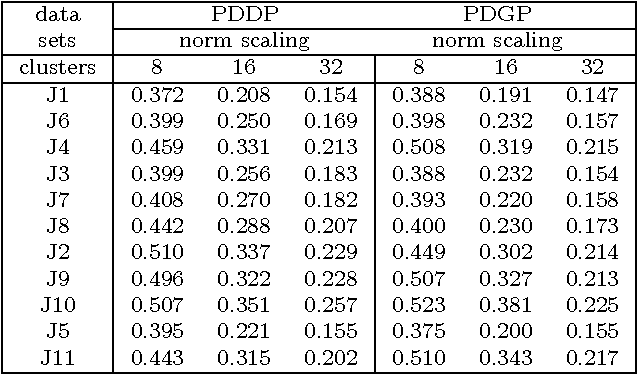
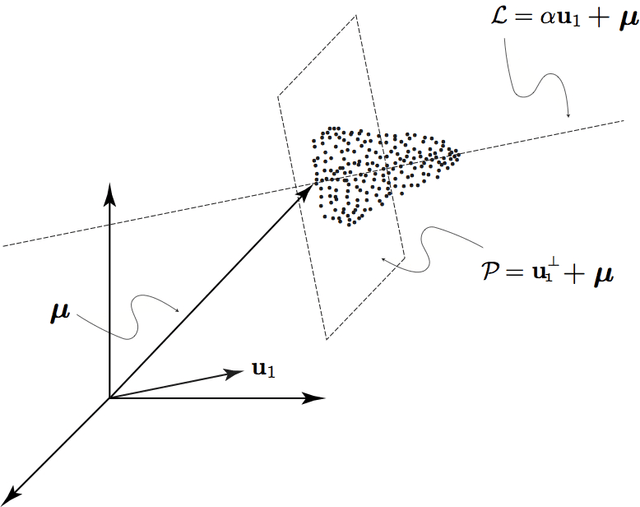
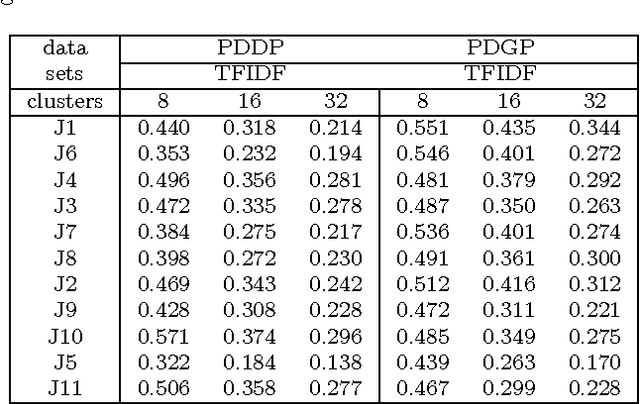
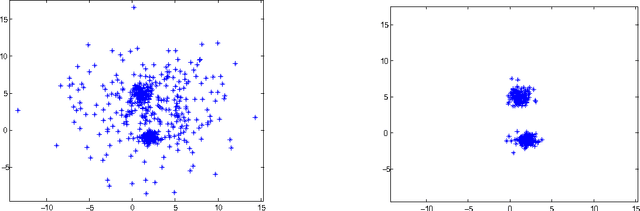
We explore the geometrical interpretation of the PCA based clustering algorithm Principal Direction Divisive Partitioning (PDDP). We give several examples where this algorithm breaks down, and suggest a new method, gap partitioning, which takes into account natural gaps in the data between clusters. Geometric features of the PCA space are derived and illustrated and experimental results are given which show our method is comparable on the datasets used in the original paper on PDDP.