A Flexible Iterative Framework for Consensus Clustering
Paper and Code
Aug 05, 2014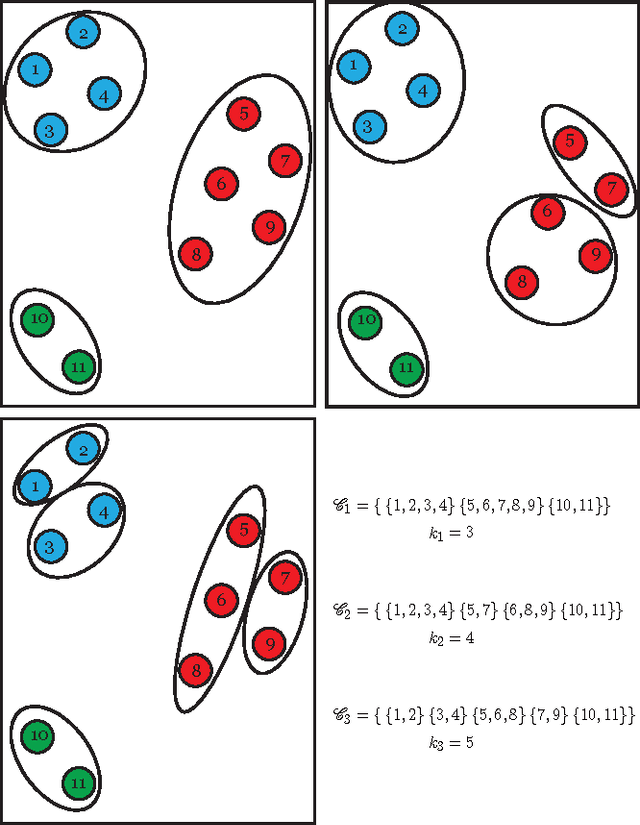

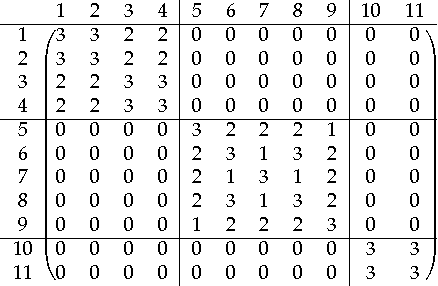
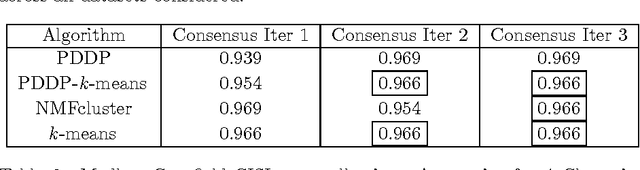
A novel framework for consensus clustering is presented which has the ability to determine both the number of clusters and a final solution using multiple algorithms. A consensus similarity matrix is formed from an ensemble using multiple algorithms and several values for k. A variety of dimension reduction techniques and clustering algorithms are considered for analysis. For noisy or high-dimensional data, an iterative technique is presented to refine this consensus matrix in way that encourages algorithms to agree upon a common solution. We utilize the theory of nearly uncoupled Markov chains to determine the number, k , of clusters in a dataset by considering a random walk on the graph defined by the consensus matrix. The eigenvalues of the associated transition probability matrix are used to determine the number of clusters. This method succeeds at determining the number of clusters in many datasets where previous methods fail. On every considered dataset, our consensus method provides a final result with accuracy well above the average of the individual algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge